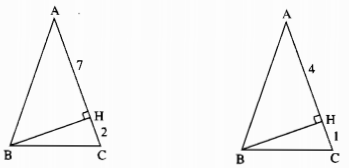
Câu 89 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1Tính cạnh đáy BC của tam giác cân ABC. Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. a) Trên hình bên trái: AH = 7cm, HC = 2cm b) Trên hình bên phải: AH = 4cm, HC = 1cm
Giải a) ∆ABC cân tại A, ta có: AB = AC = 2 + 7 = 9 Trong tam giác vuông BHA, ta có \(\widehat {BHA} = 90^\circ \) Áp dụng định lý Pytago, ta có: \(A{B^2} = B{H^2} + H{A^2}\) Suy ra: \(B{H^2} = A{B^2} - A{H^2} = {9^2} - {7^2} = 81 - 49 = 32\) Trong tam giác vuông BHC, ta có \(\widehat {BHC} = 90^\circ \) Áp dụng định lý Pytago, ta có: \(B{C^2} = B{H^2} + H{C^2}\) \(B{C^2} = 32 + {2^2} = 36 \Rightarrow BC = 6\) b) ∆ABC cân tại A nên ta có: AB = AC = 4 +1 = 5 Trong tam giác vuông BHA, ta có: \(\widehat {BHA} = 90^\circ \) Áp dụng định lý Pytago, ta có: \(A{B^2} = B{H^2} + H{A^2}\) Suy ra: \(B{H^2} = A{B^2} - H{A^2} = {5^2} - {4^2} = 25 - 16 = 9\) Trong tam giác vuông BHC, ta có \(\widehat {BHC} = 90^\circ \) Áp dụng định lý Pytago, ta có: \(B{C^2} = B{H^2} + H{C^2}\) \(B{C^2} = 9 + {1^2} = 10 \Rightarrow BC = \sqrt {10} \) Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 7: Định lí Py-ta-go
|
-
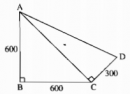
Câu 90 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1
So sánh quãng đường lúc đi và quãng đường lúc về của An, quãng đường nào dài hơn.
-

Câu 91 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Hãy chọn ra các bộ ba có thể là độ dài ba cạnh của một tam giác vuông.
-
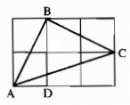
Câu 92 trang 150 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình 67) là tam giác vuông cân.

 Tải ngay
Tải ngay