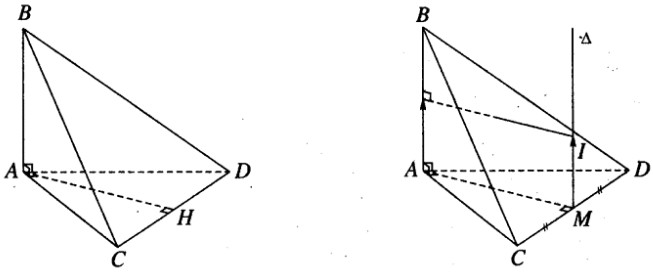
Đề 3 trang 135 Sách bài tập (SBT) Hình học 12

ĐỀ 3 (45 PHÚT)

Trang 135 sách bài tập (SBT) – Hình học 12

Trong không gian Oxyz cho bốn điểm A(2; 4; -1),B(1; 4; -1),C(2; 4; 3), D(2; 2; -1).

a) (2 điểm) Chứng minh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một.

b) (2 điểm) Viết phương trình tham số của đường vuông góc chung \(\Delta \) của hai đường thẳng AB và CD.

c) (3 điểm) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D.

d) (3 điểm) Viết phương trình mặt phẳng \((\alpha )\) tiếp xúc với mặt cầu (S) và song song với mặt phẳng (ABD).

Hướng dẫn làm bài

a) Ta có \(\overrightarrow {AB}  = ( - 1;0;0);\overrightarrow {AC}  = (0;0;4);\overrightarrow {AD}  = (0; - 2;0)\)

\(\overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AC} .\overrightarrow {AD}  = \overrightarrow {AD} .\overrightarrow {AB}  = 0\) , suy ra  \(AB \bot AC,AC \bot AD,AD \bot AB\)

Vậy AB, AC, AD vuông góc với nhau từng đôi một.

b) Gọi H là hình chiếu vuông góc của A trên CD. Ta có AH chính là đường vuông góc chung của AB và CD (hình 3.34)

\(\overrightarrow {AB}  = ( - 1;0;0);\overrightarrow {CD}  = (0; - 2; - 4)\)

Vecto chỉ phương của đường thẳng AH là \(\overrightarrow a  = \overrightarrow {AB}  \wedge \overrightarrow {CD}  = (0; - 4;2)\).

Phương trình tham số của đường thẳng AH hay \(\Delta \) là \(\left\{ {\matrix{{x = 2} \cr {y = 4 - 4t} \cr {z = - 1 + 2t} \cr} } \right.\)

c) Gọi M trung điểm của CD. Vẽ trục \(\Delta \)  của đường tròn (ACD), mặt phẳng trung trực của AB cắt \(\Delta \) tại I(a; b; c). Ta có I là tâm của mặt cầu (S) ngoại tiếp tứ diện ABCD  (h.3.35)

Ta có M(2; 3; 1), \(\overrightarrow {MI} = {1 \over 2}\overrightarrow {AB} \Rightarrow  \left\{ {\matrix{{a - 2 = - {1 \over 2}} \cr {b - 3 = 0} \cr {c - 1 = 0} \cr} } \right. \Rightarrow \left\{ {\matrix{{a = {3 \over 2}} \cr {b = 3} \cr {c = 1} \cr} } \right.\)

(S) có bán kính \(r = IA = \sqrt {{1 \over 4} + 1 + 4}  = {{\sqrt {21} } \over 2}\)

Vậy phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD là:

 \({(x - {3 \over 2})^2} + {(y - 3)^2} + {(z - 1)^2} = {{21} \over 4}\)

d) Mặt phẳng \((\alpha )\) song song với (ABD) nên có vecto pháp tuyến là \(\overrightarrow {AC}  = (0;0;4)\)  hay \(\overrightarrow n  = (0;0;1)\)

Phương trình  \((\alpha )\) có dạng z + D = 0. Ta có: 

 \((\alpha )\) tiếp xúc với S(I, r)  \( \Leftrightarrow d(I,(\alpha )) = r \Leftrightarrow |1 + D| = {{\sqrt {21} } \over 2} \Leftrightarrow  \left[ {\matrix{{D = {{\sqrt {21} } \over 2} - 1} \cr {D = - {{\sqrt {21} } \over 2} - 1} \cr} } \right.\)

Vậy có hai mặt phẳng  \((\alpha )\) thỏa mãn đề bài là: \(({\alpha _1}):z + {{\sqrt {21} } \over 2} - 1 = 0\)  và \(({\alpha _2}):z - {{\sqrt {21} } \over 2} - 1 = 0\)

Sachbaitap.com