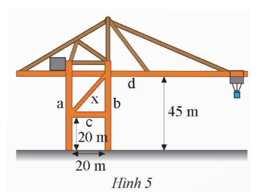
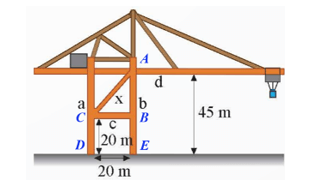
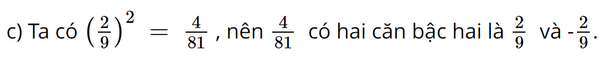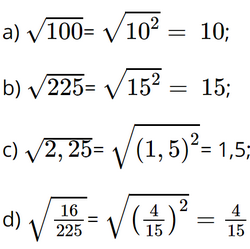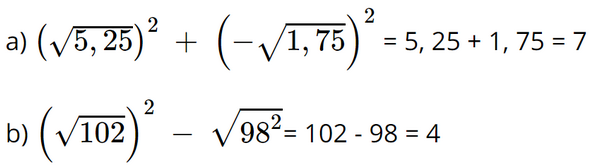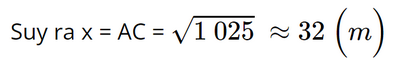Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 41 SGK Toán 9 Chân trời sáng tạo tập 1Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)? Bài 1 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Tìm các căn bậc hai của mỗi số sau: a) 16 b) 2500 c) \(\frac{4}{{81}}\) d) 0,09 Phương pháp: Dựa vào VD1 trang 38 và làm tương tự. Lời giải: a) Ta có 42 = 16, nên 16 có hai căn bậc hai là 4 và −4. b) Ta có 502 = 2 500, nên 2 500 có hai căn bậc hai là 50 và −50. d) Ta có 0,32 = 0,09, nên 0,09 có hai căn bậc hai là 0,3 và −0,3. Bài 2 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Tính a) \(\sqrt {100} \) b) \(\sqrt {225} \) c) \(\sqrt {2,25} \) d) \(\sqrt {\frac{{16}}{{225}}} \) Phương pháp: Dựa vào VD3 trang 38 và làm tương tự. Lời giải:
Bài 3 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Biết rằng 252 = 625, tìm các căn bậc hai của các số 625 và 0,0625 Phương pháp: Dựa vào VD1 trang 38 và làm tương tự. Lời giải: Vì 252 = 625 nên 625 có hai căn bậc hai là 25 và –25. Khi đó, 0,0625 có hai căn bậc hai là 0,25 và –0,25. Bài 4 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Sử dụng máy tính cầm tay, tính (kết quả làm tròn đế chữ số thập phân thứ tư): a) \(\sqrt {54} \) b) \(\sqrt {24,68} \) c) \(\sqrt 5 + \sqrt 6 + \sqrt 7 \) Phương pháp: Sử dụng máy tính cầm tay bỏ túi. Lời giải:
Bài 5 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Tính giá trị của các biểu thức: a) \({\left( {\sqrt {5,25} } \right)^2} + {\left( { - \sqrt {1,75} } \right)^2}\) b) \({\left( {\sqrt {102} } \right)^2} + \sqrt {{{98}^2}} \) Phương pháp: Dựa vào VD4 trang 38 và làm tương tự. Lời giải:
Bài 6 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Tìm x, biết: a) x2 = 121 b) 4x2 = 9 c) x2 = 10 Phương pháp: - Đưa vế phải về bình phương của một số - Lấy căn bậc hai của cả hai vế để tìm x. Lời giải: a) x2 = 121 x2 = 112 = (−11)2 x = 11 hoặc x = −11. Vậy x ∈ {−11; 11}. b) 4x2 = 9
Bài 7 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Tính giá trị của các biểu thức sau khi x = 16; y = 9 a) \(\sqrt x + \sqrt y \) b) \(\sqrt {x + y} \) c) \(\frac{1}{2}\sqrt {xy} \) d) \(\frac{1}{6}x\sqrt y \) Phương pháp: Thay giá trị x và y vào từng biểu thức để tính. Lời giải:
Bài 8 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Cho biểu thức P = \(\sqrt {{x^2} - xy + 1} \). Tính giá trị của P khi: a) x = 3; y = - 2 b) x = 1; y = 4 Phương pháp: Thay giá trị x và y vào từng biểu thức để tính. Lời giải: a) Thay x = 3, y = −2 vào biểu thức P, ta có:
Vậy khi x = 16, y = 9 giá trị của các biểu thức bằng 5.
Bài 9 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?
Phương pháp: Dựa vào định lí Pythagore trong tam giác vuông để tìm xà chéo x. Lời giải: Gọi các điểm A, B, C, D, E như trên hình vẽ.
Vì hai trụ a và b đứng cách nhau 20 m nên DE = BC = 20 m. Vì xà ngang d có độ cao 45 m so với mặt đất nên AE = 45 m. Suy ra AB = AE – BE = 45 – 20 = 25 (m). Áp dụng định lí Pythagore vào tam giác ABC vuông tại B, ta có: AC2 = AB2 + BC2 = 252 + 202 = 1025.
Vậy xà chéo x có độ dài khoảng 32 mét (làm tròn đến hàng đơn vị). Sachbaitap.com
Xem thêm tại đây:
Bài 1: Căn bậc hai
|
-

Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 45 SGK Toán 9 Chân trời sáng tạo tập 1
Một khối hình lập phương có thể tích 1000 cm3 . Chia khối gỗ này thành 8 khối gỗ hình lập phương nhỏ có thể tích bằng nhau. Tính độ dài cạnh của mỗi khối gỗ hình lập phương nhỏ.

 Tải ngay
Tải ngay