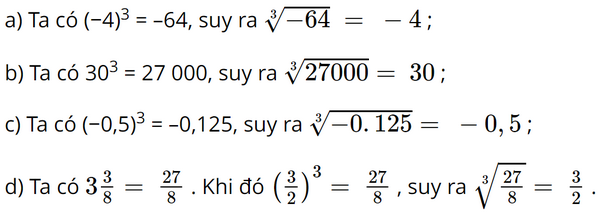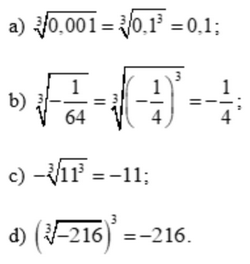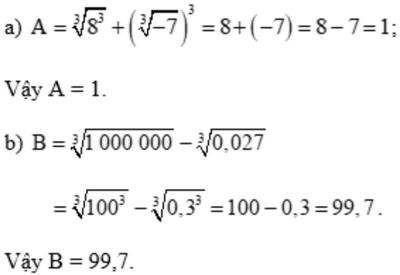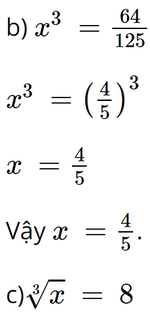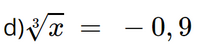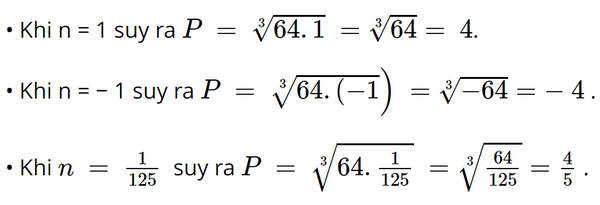Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 45 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tìm căn bậc ba của mỗi số sau:

a) -64

b) 27000

c) – 0,125

d) \(3\frac{3}{8}\)

Phương pháp:

Dựa vào VD1 trang 42 làm tương tự.

Lời giải:

Bài 2 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

a) \(\sqrt[3]{{0,001}}\)

b) \(\sqrt[3]{{ - \frac{1}{{64}}}}\)

c) \( - \sqrt[3]{{{{11}^3}}}\)

d) \({\left( {\sqrt[3]{{ - 216}}} \right)^3}\)

Phương pháp:

Dựa vào VD3 trang 38 và làm tương tự.

Lời giải:

Bài 3 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Hoàn thành bảng sau vào vở:

Phương pháp:

Dựa vào phần a, b VD2 trang 43 làm tương tự.

Lời giải:

Bài 4 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Sử dụng máy tính cầm tay, tính (kết quả làm tròn đến chữ số thập phân thứ ba):

a) \(\sqrt[3]{{79}}\)

b) \(\sqrt[3]{{ - 6,32}}\)

c) \(\frac{{\sqrt[3]{{19}} + \sqrt[3]{{20}}}}{2}\)

Phương pháp:

Sử dụng máy tính cầm tay bỏ túi.

Lời giải:

Bài 5 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính giá trị của các biểu thức:

a) A = \(\sqrt[3]{{{8^3}}} + {\left( {\sqrt[3]{{ - 7}}} \right)^3}\)

b) B = \(\sqrt[3]{{1000000}} - \sqrt[3]{{0,027}}\)

Phương pháp:

Dựa vào phần c VD2 trang 43 làm tương tự.

Lời giải:

Bài 6 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tìm x, biết:

a) x³ = - 27

b) x³ = \(\frac{{64}}{{125}}\)

c) \(\sqrt[3]{x} = 8\)

d) \(\sqrt[3]{x} =  - 0,9\)

Phương pháp:

-  Đưa vế phải về lập phương của một số

-  Lấy căn bậc ba của cả hai vế để tìm x.

Lời giải:

a) x³ = –27

x³ = (–3)³

x = –3.

Vậy x = –3.

a) x³ = –27

x³ = (–3)³

x = –3.

Vậy x = –3.

x = (–0,9)³

x = –0,729.

Vậy x = –0,729.

Bài 7 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính giá trị của biểu thức P = \(\sqrt[3]{{64n}}\) khi n = 1; n = - 1; n = \(\frac{1}{{125}}\).

Phương pháp:

Thay lần lượt giá trị n để tính.

Lời giải:

Bài 8 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo

Một khối hình lập phương có thể tích 1000 cm³ . Chia khối gỗ này thành 8 khối gỗ hình lập phương nhỏ có thể tích bằng nhau. Tính độ dài cạnh của mỗi khối gỗ hình lập phương nhỏ.

Phương pháp:

-  Tìm thể tích của khối gỗ hình lập phương nhỏ

-  Dựa vào công thức tính thể tích lập phương V = cạnh.cạnh.cạnh để suy ra độ dài cạnh.

Lời giải:

Vậy độ dài của mỗi khối gỗ hình lập phương nhỏ là 5 cm.

Sachbaitap.com