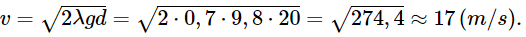Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 59, 60 SGK Toán 9 Cánh Diều tập 1Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a. Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua: Q = I2Rt Bài 1 trang 59 SGK Toán 9 tập 1 - Cánh Diều Tính: a. \(\sqrt {{{25}^2}} \); b. \(\sqrt {{{\left( { - 0,16} \right)}^2}} \); c. \(\sqrt {{{\left( {\sqrt 7 - 3} \right)}^2}} \). Phương pháp: Sử dụng tính chất căn bậc hai của một bình phương để giải bài toán. Lời giải:
Bài 2 trang 59 SGK Toán 9 tập 1 - Cánh Diều Áp dụng quy tắc về căn bậc hai của một tích, hãy tính: a. \(\sqrt {36.81} \) b. \(\sqrt {49.121.169} \) c. \(\sqrt {{{50}^2} - {{14}^2}} \) d. \(\sqrt {3 + \sqrt 5 } .\sqrt {3 - \sqrt 5 } \) Phương pháp: Áp dụng quy tắc về căn bậc hai của một tích để tính. Lời giải:
Bài 3 trang 59 SGK Toán 9 tập 1 - Cánh Diều Áp dụng quy tắc về căn bậc hai của một thương, hãy tính: a. \(\sqrt {\frac{{49}}{{36}}} \) b. \(\sqrt {\frac{{{{13}^2} - {{12}^2}}}{{81}}} \) c. \(\frac{{\sqrt {{9^3} + {7^3}} }}{{\sqrt {{9^2} - 9.7 + {7^2}} }}\) d. \(\frac{{\sqrt {{{50}^3} - 1} }}{{\sqrt {{{50}^2} + 51} }}\) Phương pháp: Áp dụng quy tắc về căn bậc hai của một thương để tính. Lời giải:
Bài 4 trang 59 SGK Toán 9 tập 1 - Cánh Diều Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai, hãy rút gọn biểu thức: a. \(\sqrt {12} - \sqrt {27} + \sqrt {75} \); b. \(2\sqrt {80} - 2\sqrt 5 - 3\sqrt {20} \); c. \(\sqrt {2,8} .\sqrt {0,7} \). Phương pháp: Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai để xử lý bài toán. Lời giải:
Bài 5 trang 59 SGK Toán 9 tập 1 - Cánh Diều Áp dụng quy tắc đưa thừa số vào trong dấu căn bậc hai, hãy rút gọn biểu thức: a. \(9\sqrt {\frac{2}{9}} - 3\sqrt 2 \) b. \(\left( {2\sqrt 3 + \sqrt {11} } \right)\left( {\sqrt {12} - \sqrt {11} } \right)\) Phương pháp: Áp dụng quy tắc đưa thừa số vào trong dấu căn để xử lý bài toán. Lời giải:
Bài 6 trang 59 SGK Toán 9 tập 1 - Cánh Diều So sánh: a. \(\sqrt 3 .\sqrt 7 \) và \(\sqrt {22} \); b. \(\frac{{\sqrt {52} }}{{\sqrt 2 }}\) và \(5\); c. \(3\sqrt 7 \) và \(\sqrt {65} \). Phương pháp: Áp dụng các quy tắc về căn bậc hai để đưa các biểu thức về trong căn rồi so sánh. Lời giải:
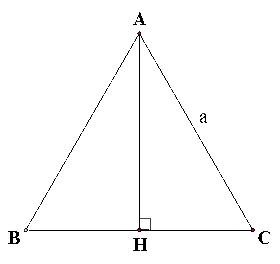
Bài 7 trang 60 SGK Toán 9 tập 1 - Cánh Diều Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a. Phương pháp: Kết hợp với các kiến thức hình học cùng phép tính của căn thức để giải bài toán Lời giải:
Xét ∆ABC đều có AH là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó H là trung điểm của BC. Suy ra Xét ∆AHC vuông tại H, theo định lí Pythagore, ta có: AC2 = AH2 + HC2
Vậy độ dài đường cao AH của tam giác ABC là Bài 8 trang 60 SGK Toán 9 tập 1 - Cánh Diều Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua: \(Q = {I^2}Rt\). Trong đó: Q là nhiệt lượng tỏa ra trên dây dẫn tính theo Jun (J); I là cường độ dòng điện chạy trong dây dẫn tính theo Ampe (A); R là điện trở dây dẫn tính theo Ohm \(\left( \Omega \right)\); t là thời gian dòng điện chạy qua dây dẫn tính theo giây. Áp dụng công thức trên để giải bài toán sau: Một bếp điện khi hoạt động bình thường có điện trở \(R = 80\Omega \). Tính cường độ dòng điện chạy trong dây dẫn, biết nhiệt lượng mà dây dẫn tỏa ra trong 1 giây là 500J.
Thay số rồi áp dụng các quy tắc của căn thức để tìm I. Lời giải: Theo bài, ta có R = 80 (Ω), t = 1 (s) và Q = 500 (J). Áp dụng công thức Q = I2RT, ta có: 500 = I2.80.1 Suy ra 80I2 = 500, nên Do đó Vậy cường độ dòng điện chạy trong dây dẫn là 2,5 Ampe. Bài 9 trang 60 SGK Toán 9 tập 1 - Cánh Diều Tốc độ gần đúng của một ô tô ngay trước khi đạp phanh được tính theo công thức \(v = \sqrt {2\lambda gd} \), trong đó \(v\left( {m/s} \right)\) là tốc độ của ô tô, \(d\left( m \right)\) là chiều dài của vết trượt tính từ thời điểm đạp phanh cho đến khi ô tô dừng lại trên đường, \(\lambda \) là hệ số cản lăn của mặt đường, \(g = 9,8m/{s^2}\). Nếu một ô tô để lại vết trượt dài khoảng 20m trên đường nhựa thì tốc độ của ô tô trước khi đạp phanh là khoảng bao nhiêu mét trên giây (làm tròn đến kết quả đến hàng đơn vị)? Biết rằng hệ số cản lăn của đường nhựa là \(\lambda = 0,7\).
Thay số vào công thức rồi áp dụng các quy tắc của căn thức để tìm v. Lời giải: Theo bài, ta có λ = 0,7; d = 20 (m) ; g = 9,8 m/s2. Do đó tốc độ của ô tô đó trước khi đạp phanh là:
Vậy tốc độ của ô tô trước khi đạp phanh là khoảng 17 m/s. Sachbaitap.com
Xem thêm tại đây:
Bài 2: Một số phép tính về căn bậc hai của số thực
|
-

Giải bài 1, 2, 3, 4, 5, 6, 7 trang 65, 66 SGK Toán 9 Cánh Diều tập 1
Chiều cao ngang vai của một con voi đực ở châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức: (h = 62,5.sqrt[3]{t} + 75,8) với t là tuổi của con voi tính theo năm.a. Một con voi đực 8 tuổi có chiều cao ngang vai là bao nhiêu centimét?

 Tải ngay
Tải ngay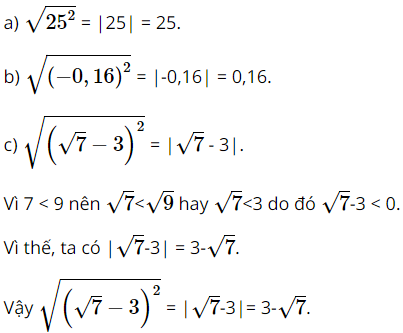
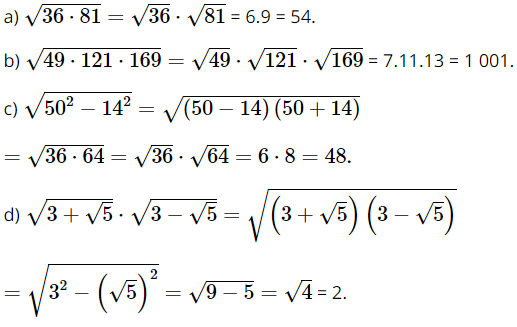
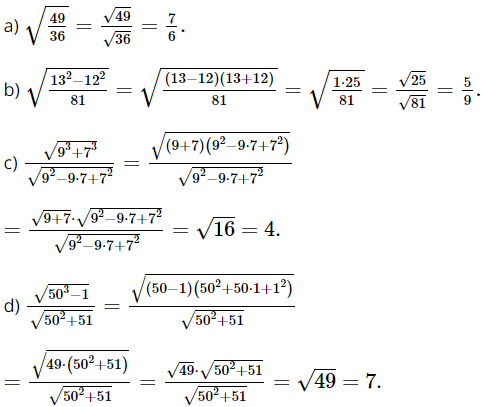
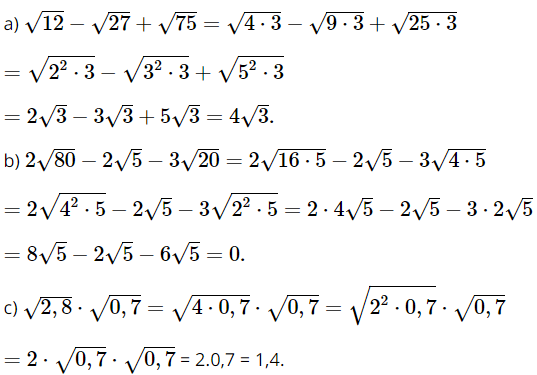
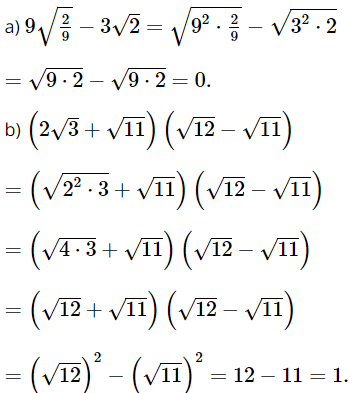

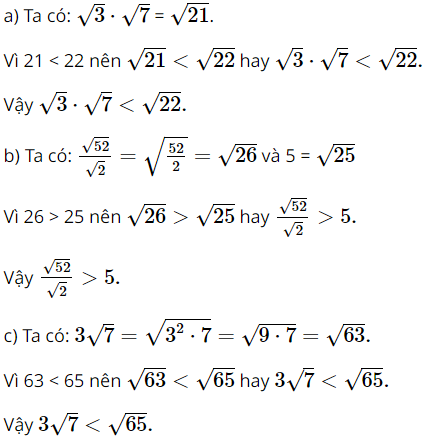
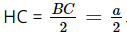
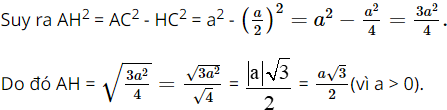
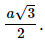
 Phương pháp:
Phương pháp: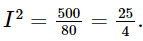
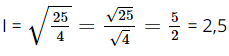

 Phương pháp:
Phương pháp: