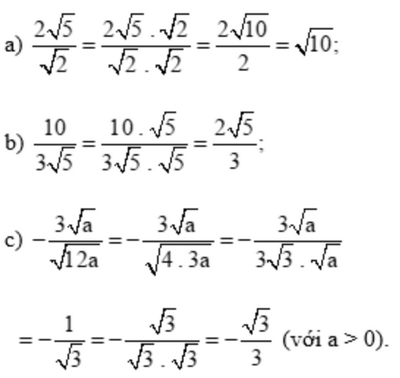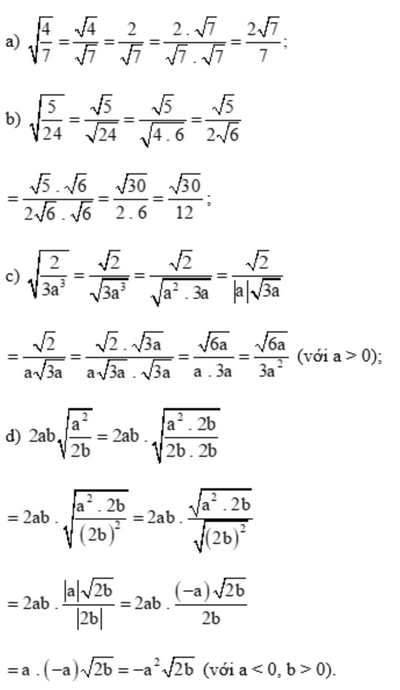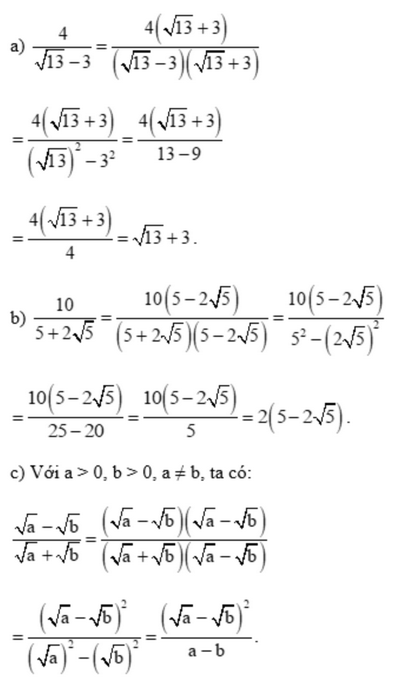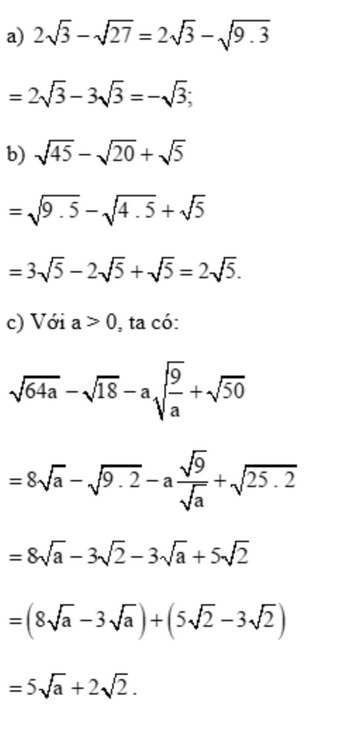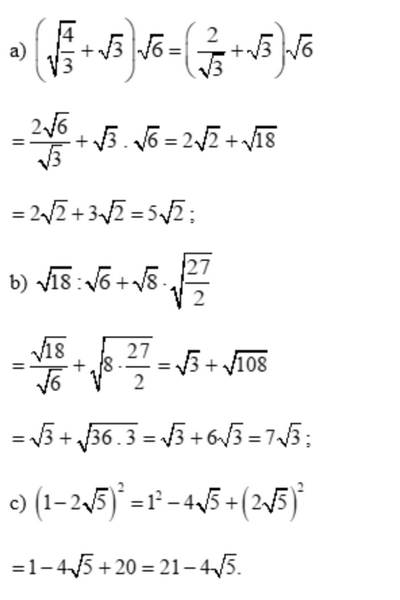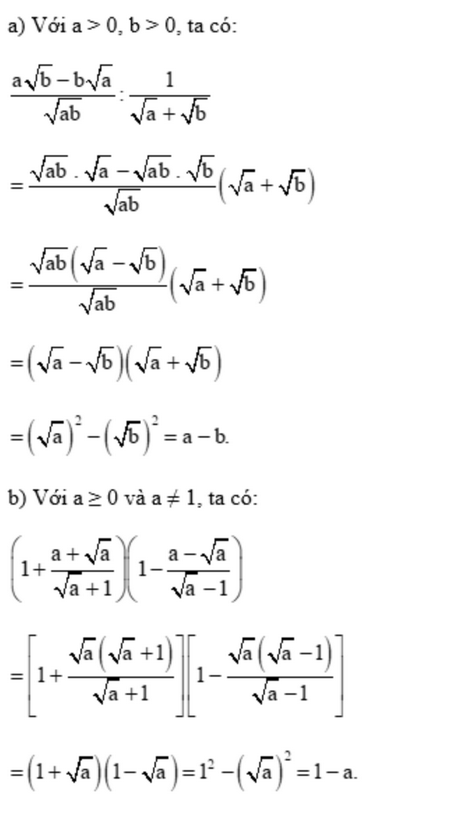Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 56 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trục căn thức ở mẫu các biểu thức sau:

a) \(\frac{{2\sqrt 5 }}{{\sqrt 2 }}\)

b) \(\frac{{10}}{{3\sqrt 5 }}\)

c) \( - \frac{{3\sqrt a }}{{\sqrt {12} a}}\) với a > 0

Phương pháp:

Dựa vào VD1 trang 53 làm tương tự.

Lời giải:

Bài 2 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

Khử mẫu của biểu thức lấy căn:

a) \(\sqrt {\frac{4}{7}} \)

b) \(\sqrt {\frac{5}{{24}}} \)

c) \(\sqrt {\frac{2}{{3{a^3}}}} \) với a > 0

d) \(2ab\sqrt {\frac{{{a^2}}}{{2b}}} \) với a < 0, b > 0

Phương pháp:

Dựa vào VD2 trang 53 làm tương tự.

Lời giải:

Bài 3 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trục căn thức ở mẫu các biểu thức sau:

a) \(\frac{4}{{\sqrt {13}  - 3}}\)

b) \(\frac{{10}}{{5 + 2\sqrt 5 }}\)

c) \(\frac{{\sqrt a  - \sqrt b }}{{\sqrt a  + \sqrt b }}\) với a > 0; b > 0, \(a \ne b\).

Phương pháp:

Dựa vào VD3 trang 53 làm tương tự.

Lời giải:

Bài 4 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) \(2\sqrt 3  - \sqrt {27} \)

b) \(\sqrt {45}  - \sqrt {20}  + \sqrt 5 \)

c) \(\sqrt {64a}  - \sqrt {18}  - a\sqrt {\frac{9}{a}}  + \sqrt {50} \) với a > 0

Phương pháp:

Dựa vào VD5 trang 55 làm tương tự.

Lời giải:

Bài 5 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

a) \(\left( {\sqrt {\frac{4}{3}}  + \sqrt 3 } \right)\sqrt 6 \)

b) \(\sqrt {18} :\sqrt 6  + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)

c) \({\left( {1 - 2\sqrt 5 } \right)^2}\)

Phương pháp:

Dựa vào VD5 trang 55 làm tương tự.

Lời giải:

Bài 6 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Chứng minh rằng:

a) \(\frac{{a\sqrt b  - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a  + \sqrt b }} = a - b\) với a > 0; b > 0

b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a  + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a  - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1

Phương pháp:

Phân tích xuất hiện nhân tử chung, tính toán vế trái rồi tính đưa về dạng vế phải.

Lời giải:

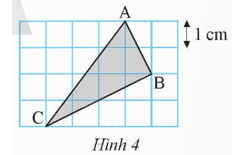
Bài 7 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tam giác ABC được vẽ trên ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC

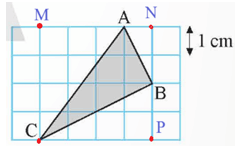
Phương pháp:

Nhìn vào hình ta xét tam giác vuông ABC biết được độ dài các cạnh sau đó áp dụng công thức chu vi tam giác = AB + BC + AC và diện tích tam giác = \(\frac{1}{2}AB.BC\)

Lời giải:

Gọi các điểm M, N, P như hình vẽ.

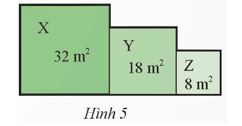
Độ dài mỗi cạnh của lưới ô vuông bằng 1 cm.

Hình vuông MNPC chứa tam giác ABC có độ dài mỗi cạnh bằng 4 cm.

Diện tích hình vuông MNPC là: S_MNPC = 4² = 16 (cm²).

• Xét tam giác AMC có AM = 3 cm, CM = 4 cm.

Áp dụng định lí Pythagore, ta có: AC² = AM² + CM² = 3² + 4² = 25.

Suy ra AC = 5 cm.

Bài 8 trang 56 SGK Toán 9 tập 1 - Chân trời sáng tạo

Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.

Phương pháp:

-  Từ diện tích S = a² (a: độ dài cạnh) từng hình vuông ta tìm được lần lượt cạnh của từng hình vuông

-  Sau đó tính chu vi của từng hình vuông rồi cộng cá kết quả với nhau.

Lời giải:

Sachbaitap.com