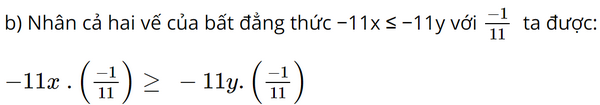Giải bài 1, 2, 3, 4, 5 trang 28 SGK Toán 9 Chân trời sáng tạo tập 1Tìm lỗi sai trong lập luận sau: Bạn Trang nhỏ tuổi hơn bạn Mai, bạn Mai nhẹ cân hơn bạn Tín. Gọi a và b lần lượt là số tuổi của bạn Trang và bạn Mai; b và c là số cân nặng của bạn Mai và bạn Tín. Vì a < b và b < c nên theo tính chất bắc cầu ta suy ra a < c. Vậy bạn Trang nhỏ tuổi hơn bạn Tín. Bài 1 trang 28 SGK Toán 9 tập 1 - Chân trời sáng tạo Dùng các dấu >,<,\( \ge \), \( \le \) để diễn tả: a) Tốc độ v đúng quy định với biển báo giao thông ở Hình 4a b) Trọng tải P của toàn bộ xe khi đi qua cầu đúng quy định với biển báo giao thông ở Hình 4b.
Phương pháp: Đọc kĩ từng câu để diễn tả bằng bất đẳng thức. Lời giải: a) Trong Hình 4a, biển báo chỉ tốc độ tối đa cho phép là 70 km/h. Do đó ta có v ≤ 70. b) Trong Hình 4a, biển báo chỉ trọng tải P của toàn bộ xe khi đi qua cầu không vượt quá 10 tấn. Do đó ta có P ≤ 10. Bài 2 trang 28 SGK Toán 9 tập 1 - Chân trời sáng tạo Hãy chỉ ra các bất đẳng thức diễn tả mỗi khẳng định sau: a) m lớn hơn 8 b) n nhỏ hơn 21 c) x nhỏ hơn hoặc bằng 4 d) y lớn hơn hoặc bằng 0. Phương pháp: Đọc kĩ từng câu để diễn tả bằng bất đẳng thức. Lời giải: a) Bất đẳng thức diễn tả m lớn hơn 8 là: m > 8. b) Bất đẳng thức diễn tả n nhỏ hơn 21 là: n < 21. c) Bất đẳng thức diễn tả x nhỏ hơn hoặc bằng 4 là: x ≤ 4. d) Bất đẳng thức diễn tả y lớn hơn hoặc bằng 0 là: y ≥ 0. Bài 3 trang 28 SGK Toán 9 tập 1 - Chân trời sáng tạo Hãy cho biết các bất đẳng thức được tạo thành khi: a) Cộng hai vế của bất đẳng thức m > 5 với – 4; b) Cộng hai vế của bất đẳng thức x2 \( \le \) y + 1 với 9; c) Nhân hai vế của bất đẳng thức x > 1 với 3, rồi tiếp tục cộng với 2; d) Cộng hai vế của bất đẳng thức m \( \le \) - 1 với – 1, rồi tiếp tục cộng với – 7. Phương pháp: Dựa vào tính chất liên hệ giữa phép thứ tự và phép cộng: Cho ba số a, b và c. Nếu a > b thì a + c > b + c. Dựa vào tính chất liên hệ giữa thứ tự và phép nhân Cho ba số a, b, c và a > b. - Nếu c > 0 thì a.c > b.c; - Nếu c < 0 thì a.c < b.c Lời giải: a) Cộng hai vế của bất đẳng thức m > 5 với −4 ta được: m – 4 > 5 – 4 m – 4 > 1. Vậy bất đẳng thức được tạo thành là m – 4 > 1. b) Cộng hai vế của bất đẳng thức x2 ≤ y + 1 với 9 ta được: x2 + 9 ≤ y + 1 + 9 x2 + 9 ≤ y + 10. Vậy bất đẳng thức được tạo thành là x2 + 9 ≤ y + 10. c) Nhân hai vế của bất đẳng thức x > 1 với 3, rồi tiếp tục cộng với 2 ta được: 3x > 3 . 1 3x + 2 > 3 . 1 + 2 3x + 2 > 5. Vậy bất đẳng thức được tạo thành là 3x + 2 > 5. d) Cộng vào hai vế của bất đẳng thức m ≤ −1 với −1, rồi tiếp tục cộng với −7 ta được: m − 1 ≤ −1 −1 m − 1 ≤ −2 m − 1 − 7 ≤ −2 − 7 m – 8 ≤ −9 Vậy bất đẳng thức được tạo thành là m – 8 ≤ −9. Bài 4 trang 28 SGK Toán 9 tập 1 - Chân trời sáng tạo So sánh hai số x và y trong mỗi trường hợp sau: a) x + 5 > y + 5; b) – 11x \( \le \) - 11y; c) 3x – 5 < 3y – 5; d) – 7x + 1 > - 7y + 1. Phương pháp: Dựa vào tính chất liên hệ giữa phép thứ tự và phép cộng: Cho ba số a, b và c. Nếu a > b thì a + c > b + c. Dựa vào tính chất liên hệ giữa thứ tự và phép nhân Cho ba số a, b, c và a > b. - Nếu c > 0 thì a.c > b.c; - Nếu c < 0 thì a.c < b.c Lời giải: a) Cộng vào hai vế của bất đẳng thức x + 5 > y + 5 với –5 ta được: x + 5 – 5 > y + 5 – 5 x > y. Vậy x > y.
x ≥ y. Vậy x ≥ y. c) Cộng vào hai vế của bất đẳng thức 3x – 5 < 3y – 5 với 5 ta được: 3x – 5 + 5 < 3y – 5 + 5 3x < 3y.
x < y. Vậy x < y. d) Cộng vào hai vế của bất đẳng thức −7x + 1 > −7y + 1 với −1 ta được: −7x + 1 + (−1) > −7y + 1 + (−1) −7x > −7y.
Bài 5 trang 28 SGK Toán 9 tập 1 - Chân trời sáng tạo Cho hai số a, b thoả mãn a < b. Chứng tỏ: a) b – a > 0; b) a – 2 < b – 1 c) 2a + b < 3b d) – 2a – 3 > - 2b – 3. Phương pháp: Dựa vào tính chất liên hệ giữa phép thứ tự và phép cộng: Cho ba số a, b và c. Nếu a > b thì a + c > b + c. Dựa vào tính chất liên hệ giữa thứ tự và phép nhân Cho ba số a, b, c và a > b. - Nếu c > 0 thì a.c > b.c; - Nếu c < 0 thì a.c < b.c Lời giải: a) Trừ hai vế của bất đẳng thức a < b cho a, ta được: 0 < b – a hay b – a > 0 (điều phải chứng minh). b) Trừ hai vế của bất đẳng thức a < b cho 2, ta được: a – 2 < b – 2. (1) Cộng hai vế của bất đẳng thức –2 < –1 cho b, ta được: –2 + b < –1 + b hay b – 2 < b – 1. (2) Từ (1) và (2) suy ra a – 2 < b – 1 (điều phải chứng minh). c) Nhân hai vế của bất đẳng thức a < b cho 2, ta được: 2a < 2b. Cộng hai vế của bất đẳng thức 2a < 2b cho b, ta được: 2a + b < 3b (điều phải chứng minh). d) Nhân hai vế của bất đẳng thức a < b cho (–2), ta được: –2a > –2b. Cộng hai vế của bất đẳng thức –2a > –2b cho (–3), ta được: –2a – 3 > –2b – 3 (điều phải chứng minh). Câu hỏi đố vui trang 28 SGK Toán 9 tập 1 - Chân trời sáng tạo Tìm lỗi sai trong lập luận sau: Bạn Trang nhỏ tuổi hơn bạn Mai, bạn Mai nhẹ cân hơn bạn Tín. Gọi a và b lần lượt là số tuổi của bạn Trang và bạn Mai; b và c là số cân nặng của bạn Mai và bạn Tín. Vì a < b và b < c nên theo tính chất bắc cầu ta suy ra a < c. Vậy bạn Trang nhỏ tuổi hơn bạn Tín. Phương pháp: Đọc kĩ đề bài để tìm lỗi sai. Lời giải: Theo đề bài ra thì b vừa là số tuổi của bạn Mai vừa là số cân nặng của bạn Mai. Mà số tuổi và số cân nặng của bạn Mai là khác nhau. Vậy cách lập luận trên sai vì gọi số tuổi của bạn Mai và số cân nặng của bạn Mai đều là b.
Sachbaitap.com
Xem thêm tại đây:
Bài 1: Bất đẳng thức
|
-

Giải bài 1, 2, 3, 4, 5, 6 trang 34 SGK Toán 9 Chân trời sáng tạo tập 1
Một kì thi Tiếng anh bao gồm bốn kĩ năng: nghe, nói, đọc và viết. Kết quả của bài thi là điểm số trung bình của bốn kĩ năng này. Bạn Hà đã đạt được điểm số của ba kĩ năng nghe, đọc, viết lần lượt là 6,5; 6,5; 5,5. Hỏi bạn Hà cần đạt bao nhiêu điểm trong kĩ năng nói để đạt được của bài thi ít nhất là 6,25?

 Tải ngay
Tải ngay