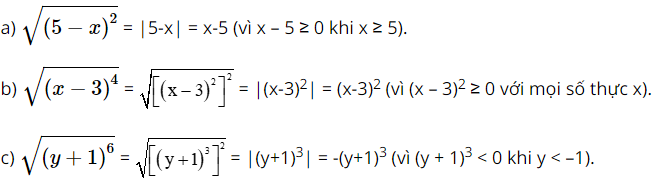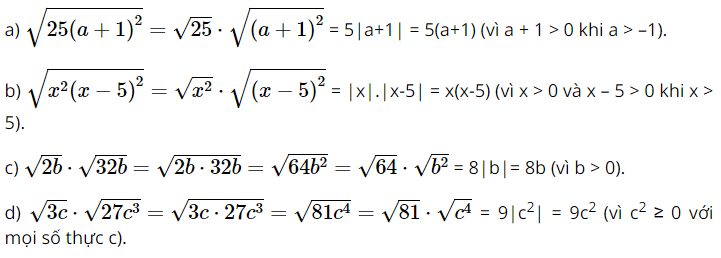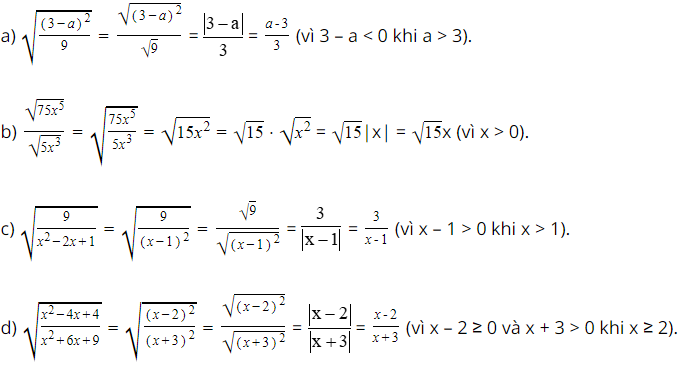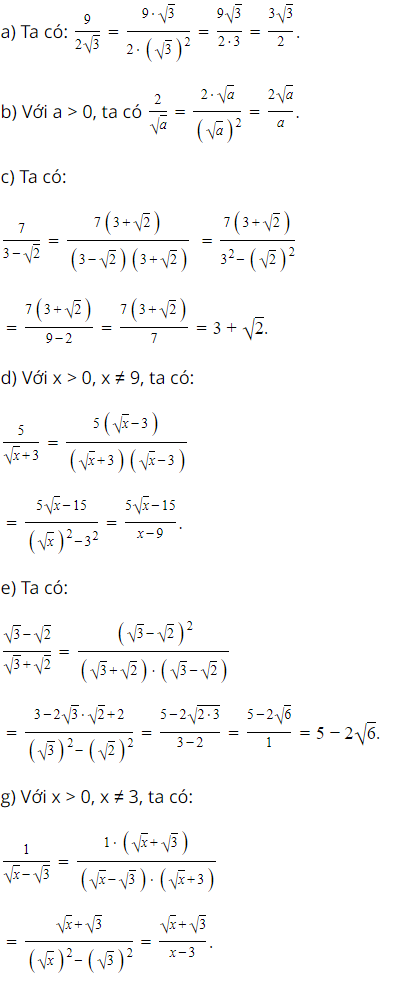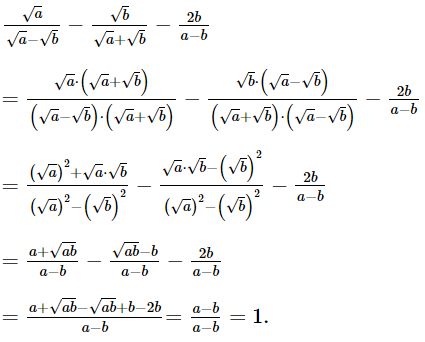Giải bài 1, 2, 3, 4, 5 trang 70, 71 SGK Toán 9 Cánh Diều tập 1

Bài 1 trang 70 SGK Toán 9 tập 1 - Cánh Diều

Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:

a. \(\sqrt {\left( {5 - x} \right)_{}^2} \) với \(x \ge 5\);

b. \(\sqrt {\left( {x - 3} \right)_{}^4} \);

c. \(\sqrt {\left( {y + 1} \right)_{}^6} \) với \(y <  - 1\).

Phương pháp:

+ Đưa bình phương về trị tuyệt đối;

+ Xét xem biểu thức trong trị tuyệt đối lớn hơn 0 hay nhỏ hơn 0;

+ Phá trị tuyệt đối.

Lời giải:

Bài 2 trang 70 SGK Toán 9 tập 1 - Cánh Diều

Áp dụng quy tắc về căn thức bậc hai của một tích, hãy rút gọn biểu thức:

a. \(\sqrt {25\left( {a + 1} \right)_{}^2} \) với \(a >  - 1\);

b. \(\sqrt {x_{}^2\left( {x - 5} \right)_{}^2} \) với \(x > 5\);

c. \(\sqrt {2b} .\sqrt {32b} \) với \(b > 0\);

d. \(\sqrt {3c} .\sqrt {27c_{}^3} \) với \(c > 0\).

Phương pháp:

Áp dụng kiến thức “Với các biểu thức A, B không âm, ta có: \(\sqrt {A.B}  = \sqrt A .\sqrt B \)” để giải bài toán.

Lời giải:

Bài 3 trang 71 SGK Toán 9 tập 1 - Cánh Diều

Áp dụng quy tắc về căn thức bậc hai của một thương, hãy rút gọn biểu thức:

a. \(\sqrt {\frac{{\left( {3 - a} \right)_{}^2}}{9}} \) với \(a > 3\);

b. \(\frac{{\sqrt {75x_{}^5} }}{{\sqrt {5x_{}^3} }}\) với \(x > 0\);

c. \(\sqrt {\frac{9}{{x_{}^2 - 2x + 1}}} \) với \(x > 1\);

d. \(\sqrt {\frac{{x_{}^2 - 4x + 4}}{{x_{}^2 + 6x + 9}}} \) với \(x \ge 2\).

Phương pháp:

+ Tách thương thành hai phép chia hoặc đưa vào cùng 1 phép chia để rút gọn cho nhau;

+ Đưa tử số và mẫu số của thương về bình phương;

+ Đưa bình phương ra ngoài dấu căn;

+ Rút gọn bình phương.

Lời giải:

Bài 4 trang 71 SGK Toán 9 tập 1 - Cánh Diều

Trục căn thức ở mẫu:

a. \(\frac{9}{{2\sqrt 3 }}\);

b. \(\frac{2}{{\sqrt a }}\) với \(a > 0\);

c. \(\frac{7}{{3 - \sqrt 2 }}\);

d. \(\frac{5}{{\sqrt x  + 3}}\) với \(x > 0;x \ne 9\);

e. \(\frac{{\sqrt 3  - \sqrt 2 }}{{\sqrt 3  + \sqrt 2 }}\);

g. \(\frac{1}{{\sqrt x  - \sqrt 3 }}\) với \(x > 0,x \ne 3\).

Phương pháp:

+ Tìm biểu thức có thể làm mất căn thức ở dưới mẫu;

+ Nhân cả tử và mẫu với biểu thức vừa tìm được để trục căn thức ở mẫu.

Lời giải:

Bài 5 trang 71 SGK Toán 9 tập 1 - Cánh Diều

Rút gọn biểu thức: \(\frac{{\sqrt a }}{{\sqrt a  - \sqrt b }} - \frac{{\sqrt b }}{{\sqrt a  + \sqrt b }} - \frac{{2b}}{{a - b}}\) với \(a \ge 0,b \ge 0,a \ne b\).

Phương pháp:

+ Trục căn thức của các phân thức;

+ Dùng phép cộng phân số để rút gọn phân thức.

Lời giải:

Với a ≥ 0, b ≥ 0, a ≠ b, ta có:

Sachbaitap.com