Giải bài 1, 2, 3, 4, 5 trang 9, 10 SGK Toán 9 Chân trời sáng tạo tập 1Một người đi xe đạp từ A đến B cách nhau 60km. Sau 1 giờ 40 phút, trên cùng quãng đường đó, một xe máy cũng đi từ A đến B và đến B sớm hơn xe đạp 1 giờ. Tính tốc độ của mỗi xe, biết rằng tốc độ của xe máy gấp 3 lần tốc độ của xe đạp. Bài 1 trang 9 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải các phương trình: a) \(5x(2x - 3) = 0\); b) \((2x - 5)(3x + 6) = 0\); c) \(\left( {\frac{2}{3}x - 1} \right)\left( {\frac{1}{2}x + 3} \right) = 0\); d) \((2,5t - 7,5)(0,2t + 5) = 0\). Phương pháp: Để giải phương trình \(\left( {{a_1}x + {b_1}} \right)\left( {{a_2}x + {b_2}} \right) = 0\), ta giải hai phương trình \({a_1}x + {b_1} = 0\) và \({a_2}x + {b_2} = 0\), rồi lấy tất cả các nghiệm của chúng. Lời giải: a) Ta có: 5x(2x – 3) = 0 5x = 0 hoặc 2x – 3 = 0 x = 0 hoặc x= Vậy phương trình đã cho có hai nghiệm là x = 0 và x = b) Ta có: (2x – 5)(3x + 6) = 0 2x – 5 = 0 hoặc 3x + 6 = 0 x= Vậy phương trình đã cho có hai nghiệm là x=
d) Ta có: (2,5t – 7,5)(0,2t + 5) = 0 2,5t – 7,5 = 0 hoặc 0,2t + 5 = 0 2,5t = 7,5 hoặc 0,2t = –5 x = 5 hoặc x = –25. Vậy phương trình đã cho có hai nghiệm là x = 5 và x = –25. Bài 2 trang 9 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải các phương trình: a) \(3x(x - 4) + 7(x - 4) = 0\); b) \(5x(x + 6) - 2x - 12 = 0\); c) \({x^2} - x - (5x - 5) = 0\); d) \({(3x - 2)^2} - {(x + 6)^2} = 0\). Phương pháp: - Biến đổi về dạng phương trình \(\left( {{a_1}x + {b_1}} \right)\left( {{a_2}x + {b_2}} \right) = 0\). - Để giải phương trình \(\left( {{a_1}x + {b_1}} \right)\left( {{a_2}x + {b_2}} \right) = 0\), ta giải hai phương trình \({a_1}x + {b_1} = 0\) và \({a_2}x + {b_2} = 0\), rồi lấy tất cả các nghiệm của chúng. Lời giải: a) Ta có: 3x(x – 4) + 7(x – 4) = 0 (x – 4)(3x + 7) = 0 x – 4 = 0 hoặc 3x + 7 = 0 x = 4 hoặc x= Vậy phương trình đã cho có hai nghiệm là x = 4 và x= b) Ta có: 5x(x + 6) – 2x – 12 = 0 5x(x + 6) – 2(x + 6) = 0 (x + 6)(5x – 2) = 0 x + 6 = 0 hoặc 5x – 2 = 0 x = –6 hoặc x= Vậy phương trình đã cho có hai nghiệm là x = –6 và x= c) Ta có: x2 – x – (5x – 5) = 0 x(x – 1) – 5(x – 1) = 0 (x – 1)(x – 5) = 0 x – 1 = 0 hoặc x – 5 = 0 x = 1 hoặc x = 5. Vậy phương trình đã cho có hai nghiệm là x = 1 và x = 5. d) Ta có: (3x – 2)2 – (x + 6)2 = 0. (3x – 2 + x + 6)(3x – 2 – x – 6) = 0. (4x + 4)(2x – 8) = 0. 8(x + 1)(x – 4) = 0. x + 1 = 0 hoặc x – 4 = 0 x = –1 hoặc x = 4. Vậy phương trình đã cho có hai nghiệm là x = –1 và x = 4. Bài 3 trang 9 SGK Toán 9 tập 1 - Chân trời sáng tạo Giải các phương trình: a) \(\frac{{x + 5}}{{x - 3}} + 2 = \frac{2}{{x - 3}}\); b) \(\frac{{3x + 5}}{{x + 1}} + \frac{2}{x} = 3\); c) \(\frac{{x + 3}}{{x - 2}} + \frac{{x + 2}}{{x - 3}} = 2\); d) \(\frac{{x + 2}}{{x - 2}} - \frac{{x - 2}}{{x + 2}} = \frac{{16}}{{{x^2} - 4}}\). Phương pháp: Để giải phương trình chứa ẩn ở mẫu, ta làm như sau: Bước 1: Tìm điều kiện xác định của phương trình. Bước 2: Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu. Bước 3: Giải phương trình vừa nhận được. Bước 4: Xét mỗi giá trị tìm được ở Bước 3, giá trị nào thỏa mãn điều kiện xác định thì đó là nghiệm của phương trình đã cho. Lời giải: a) Điều kiện xác định: x ≠ 3. Ta có: x + 5 + 2(x – 3) = 2 x + 5 + 2x – 6 = 2 3x = 3 x = 1 (thỏa mãn điều kiện xác định). Vậy nghiệm của phương trình đã cho là x = 1. b) Điều kiện xác định: x ≠ –1; x ≠ 0.
x(3x + 5) + 2(x + 1) = 3x(x + 1) 3x2 + 5x + 2x + 2 = 3x2 + 3x 5x + 2x – 3x = –2 4x = –2 x= Vậy nghiệm của phương trình đã cho là x= c) Điều kiện xác định: x ≠ 3.
x + 3 + x + 2 = 2(x – 3) 2x + 5 = 2x – 6 0x = 11. Không có giá trị x thỏa mãn. Vậy phương trình đã cho vô nghiệm. d) Điều kiện xác định: x ≠ ±2.
(x + 2)2 – (x – 2)2 = 16 (x + 2 + x – 2)(x + 2 – x + 2) = 16 2x . 4 = 16 8x = 16 x = 2. Vậy nghiệm của phương trình đã cho là x = 2. Bài 4 trang 9 SGK Toán 9 tập 1 - Chân trời sáng tạo Một người đi xe đạp từ A đến B cách nhau 60km. Sau 1 giờ 40 phút, trên cùng quãng đường đó, một xe máy cũng đi từ A đến B và đến B sớm hơn xe đạp 1 giờ. Tính tốc độ của mỗi xe, biết rằng tốc độ của xe máy gấp 3 lần tốc độ của xe đạp. Phương pháp: - Gọi tốc độ của xe đạp là \(x\) (km/h), \(x > 0\). - Biểu diễn các đại lượng liên quan theo ẩn \(x\) bằng công thức \(s = v.t\). - Dựa vào dữ kiện bài toán để lập phương trình ẩn \(x\). - Giải phương trình nhận được. Lời giải: Gọi vận tốc xe đạp là: x (km/h). (x>0) Vận tốc xe máy là: 3x(km/h) Thời gian đi của xe đạp là: Thời gian đi của xe máy là: Vì sau đó 1 giờ người khác đi xe máy từ A đến B sớm hơn người đi xe đạp 1 giờ 40 phút (hay
8x=120 x =15(thỏa mãn điều kiện xác định) Vậy vận tốc xe đạp là 15km/h. Bài 5 trang 9 SGK Toán 9 tập 1 - Chân trời sáng tạo Một xí nghiệp dự định chia đều 12 600 000 đồng để thưởng cho các công nhân tham gia hội thao nhân ngày thành lập xí nghiệp. Khi đến ngày hội thao chỉ có 80% số công nhân tham gia, vì thế mỗi người tham gia hội thao được nhận thêm 105 000 đồng. Tính số công nhân dự định tham gia lúc đầu. Phương pháp: - Gọi số công nhân dự định tham gia lúc đầu là \(x\) (người), \(x \in {\mathbb{N}^*}\). - Biểu diễn các đại lượng liên quan theo ẩn \(x\). - Dựa vào dữ kiện bài toán để lập phương trình ẩn \(x\). - Giải phương trình nhận được. Lời giải: Gọi x là số công nhân dự định tham gia lúc đầu (x ∈ ℕ*). Theo dự định, số tiền mà mỗi công nhân được chia là: Theo kế hoạch, số công nhân tham gia hội thao là: 80%x = 0,8x (công nhân).
x = 30 (thỏa mãn điều kiện). Vậy số công nhân dự định tham gia lúc đầu là 30 người. Sachbaitap.com
Xem thêm tại đây:
Bài 1: Phương trình quy về phương trình bậc nhất một ẩn
|
-

Giải bài 1, 2, 3, 4, 5 trang 14 SGK Toán 9 Chân trời sáng tạo tập 1
Cho hai đường thẳng (y = - frac{1}{2}x + 2) và y = -2x – 1.a) Vẽ hai đường thẳng đó trên cùng mặt phẳng toạ độ Oxy.b) Xác định toạ độ giao điểm A của hai đường thẳng trên. c) Tọa độ của điểm A có là nghiệm của hệ phương trình

 Tải ngay
Tải ngay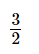
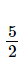
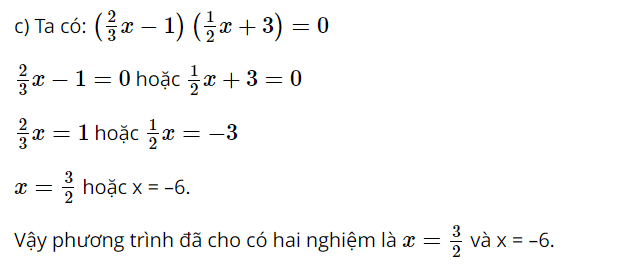
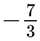
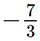
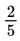

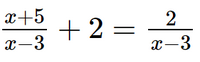
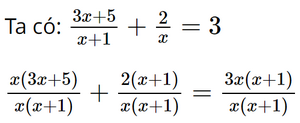
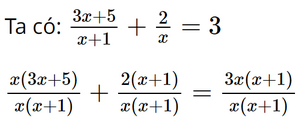
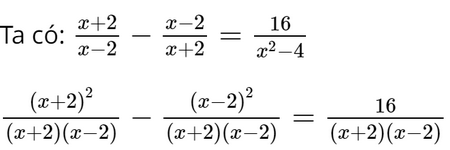
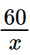
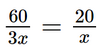 (giờ)
(giờ)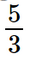
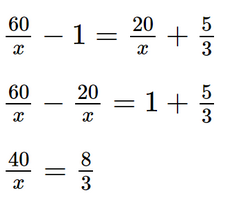
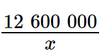 (đồng).
(đồng).