Giải bài 1.1, 1.2, 1.3, 1.4, 1.5 trang 10 SGK Toán 9 Kết nối tri thức tập 1

Bài 1.1 trang 10 SGK Toán 9 tập 1 - Kết nối tri thức

Phương trình nào sau đây là phương trình bậc nhất hai ẩn, vì sao?

a) \(5x - 8y = 0;\)

b) \(4x + 0y =  - 2;\)

c) \(0x + 0y = 1;\)

d) \(0x - 3y = 9.\)

Phương pháp:

Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\left( 1 \right)\) trong đó a,b và c là các số đã biết \(a \ne 0\) hoặc \(b \ne 0.\)

Lời giải:

a) Phương trình 5x – 8y = 0 có dạng ax + by = c với a = 5 ≠ 0, b = –8 ≠ 0.

Do đó, phương trình 5x – 8y = 0 là phương trình bậc nhất hai ẩn.

b) Phương trình 4x + 0y = –2 có dạng ax + by = c với a = 4 ≠ 0.

Do đó, phương trình 4x + 0y = –2 là phương trình bậc nhất hai ẩn.

c) Phương trình 0x + 0y = 1 có dạng ax + by = c với a = 0, b = 0.

Do đó, phương trình 0x + 0y = 1 không phải là phương trình bậc nhất hai ẩn.

d) Phương trình 0x – 3y = 9 có dạng ax + by = c với b = –3 ≠ 0.

Do đó, phương trình 0x – 3y = 9 là phương trình bậc nhất hai ẩn.

Bài 1.2 trang 10 SGK Toán 9 tập 1 - Kết nối tri thức

a) Tìm giá trị thích hợp thay cho dấu "?" trong bảng sau rồi cho biết 6 nghiệm của phương trình 2x – y = 1:

b) Viết nghiệm tổng quát của phương trình đã cho.

Phương pháp:

- Để tìm giá trị thích hợp điền vào bảng, để tìm y trong 1 cột thì ta cần thay x đã cho ở cột đấy vào \(y = 2x - 1\) để tính giá trị của y tương ứng

Ví dụ ở cột thứ 2:  \(x =  - 1 \Rightarrow y = 2.\left( { - 1} \right) - 1 =  - 3\), ta điền số -3 vào dấu ? đầu tiên.

- Cặp \(\left( {x;y} \right)\) tương ứng trong cùng 1 cột sẽ là 1 nghiệm của phương trình đã cho.

- Tìm nghiệm tổng quát bằng cách rút , ta cần rút y theo x \(\left( {by = c - ax} \right)\) từ đó ta giải được \(y = \frac{{c - ax}}{b}\) với \(b \ne 0.\) Đối với trường hợp \(b = 0\) thì ta làm ngược lại (rút x theo y). Thì nghiệm tổng quát có dạng \(\left( {x;\frac{{c - ax}}{b}} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Lời giải:

a)

• Với x = –1, ta có y = 2 . (–1) – 1 = – 2 – 1 = –3;

• Với x = –0,5, ta có y = 2 . (–0,5) – 1 = – 1 – 1 = –2;

• Với x = 0, ta có y = 2 . 0 – 1 = 0 – 1 = –1;

• Với x = 0,5, ta có y = 2 . 0,5 – 1 = 1 – 1 = 0;

• Với x = 1, ta có y = 2 . 1 – 1 = 2 – 1 = 1;

• Với x = 2, ta có y = 2 . 2 – 1 = 4 – 1 = 3.

Vậy ta có bảng sau:

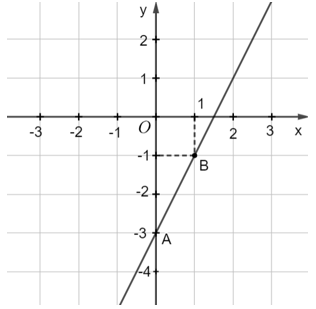
Vậy 6 nghiệm của phương trình đã cho là (–1; –3), (–0,5; –2), (0; –1), (0,5; 1), (1; 1), (2; 3).

b) Ta có y = 2x – 1. Với mỗi giá trị x tùy ý cho trước, ta luôn tìm được một giá trị y tương ứng.

Do đó, phương trình đã cho có vô số nghiệm.

Bài 1.3 trang 10 SGK Toán 9 tập 1 - Kết nối tri thức

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 2x – y = 3;

b) 0x + 2y = –4;

c) 3x + 0y = 5.

Phương pháp:

Để viết nghiệm của một phương trình bậc nhất hai ẩn, ta cần rút y theo x \(\left( {by = c - ax} \right)\) từ đó ta giải được \(y = \frac{{c - ax}}{b}\) với \(b \ne 0.\) Đối với trường hợp \(b = 0\) thì ta làm ngược lại (rút x theo y).

Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c.\)

Lời giải:

a) Xét phương trình 2x – y = 3.          (1)

Ta viết (1) dưới dạng y = 2x – 3. Mỗi cặp số (x; 2x – 3) với x ∈ ℝ tùy ý, là một nghiệm của (1).

Khi đó, ta nói phương trình (1) có nghiệm (tổng quát) là: (x; 2x – 3) với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng y = 2x – 3.

Ta xác định được hai điểm tùy ý của đường thẳng y = 2x – 3, chẳng hạn A(0; – 3), B(1; –1).

Ta biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn như sau:

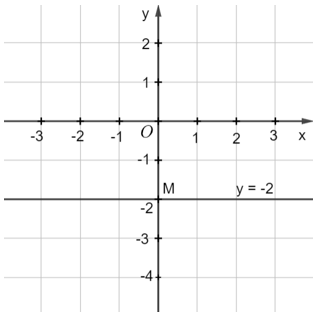
b) Xét phương trình 0x + 2y = –4 .      (2)

Ta viết gọn (2) thành y = –2. Phương trình (2) có nghiệm (x; –2) với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm M(0; –2). Ta gọi đó là đường thẳng y = –2.

Ta biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn như sau:

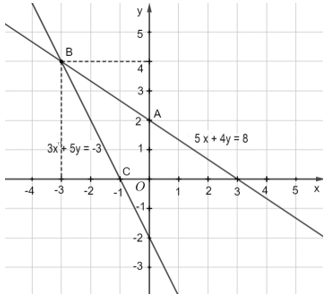
Bài 1.4 trang 10 SGK Toán 9 tập 1 - Kết nối tri thức

a) Hệ phương trình \(\left\{ \begin{array}{l}2x =  - 6\\5x + 4y = 1\end{array} \right.\) có là một hệ hai phương trình bậc nhất hai ẩn không, vì sao?

b) Cặp số \(\left( { - 3;4} \right)\) có là một nghiệm của hệ phương trình đó hay không, vì sao?

Phương pháp:

Hệ phương trình bậc nhất có dạng \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) gồm hai phương trình bậc nhất hai ẩn.

Cặp \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ khi cặp số đồng thời là nghiệm của cả 2 phương trình trong hệ.

Lời giải:

a) Hệ phương trình đã cho là hệ hai phương trình bậc nhất hai ẩn vì cả hai phương trình của hệ đã cho đều là phương trình bậc nhất hai ẩn.

b) Thay x = –3; y = 4 vào hệ phương trình đã cho, ta có:

• 2x = 2 . (−3) = −6 nên (–3; 4) là nghiệm của phương trình thứ nhất;

• 5x + 4y = 5 . (−3) + 4 . 4 = −15 + 16 = 1 nên (–3; 4) là nghiệm của phương trình thứ hai.

Do đó (–3; 4) là nghiệm chung của hai phương trình, nghĩa là (–3; 4) là một nghiệm của hệ phương trình đã cho.

Bài 1.5 trang 10 SGK Toán 9 tập 1 - Kết nối tri thức

Cho các cặp số \(\left( { - 2;1} \right),\left( {0;2} \right),\left( {1;0} \right),\left( {1,5;3} \right),\left( {4; - 3} \right)\) và hai phương trình

\(\begin{array}{l}5x + 4y = 8,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\3x + 5y =  - 3.\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)

Trong các cặp số đã cho:

a) Những cặp số nào là nghiệm của phương trình (1)?

b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?

c) Vẽ hai đường thẳng \(5x + 4y = 8\) và \(3x + 5y =  - 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.

Phương pháp:

Để kiểm tra cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình bậc nhất hai ẩn, ta thay \(x -  = {x_0};y = {y_0}\) vào phương trình cần kiểm tra, nếu kết quả luôn đúng ta được cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình bậc nhất hai ẩn.

Lời giải:

a)

• Thay x = –2; y = 1 vào phương trình (1), ta có:

5x + 4y = 5 . (–2) + 4 . 1 = −10 + 4 = −6 ≠ 8 nên (–2; 1) không phải là nghiệm của phương trình (1).

• Thay x = 0; y = 2 vào phương trình (1), ta có:

5x + 4y = 5 . 0 + 4 . 2 = 0 + 8 = 8 nên (0; 2) là nghiệm của phương trình (1).

• Thay x = 1; y = 0 vào phương trình (1), ta có:

5x + 4y = 5 . 1 + 4 . 0 = 5 + 0 = 5 ≠ 8 nên (1; 0) không phải là nghiệm của phương trình (1).

• Thay x = 1,5; y = 3 vào phương trình (1), ta có:

5x + 4y = 5 . 1,5 + 4 . 3 = 7,5 + 12 = 19,5 ≠ 8 nên (1,5; 3) không phải là nghiệm của phương trình (1).

• Thay x = 4; y = –3 vào phương trình (1), ta có:

5x + 4y = 5 . 4 + 4 . (–3) = 20 – 12 = 8 nên (4; –3) là nghiệm của phương trình (1).

Vậy cặp số là nghiệm của phương trình (1) là (0; 2) và (4; –3).

b) Để cặp số là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2) thì cặp số đó phải là nghiệm của phương trình (1). Khi đó, ta có:

• Thay x = 0; y = 2 vào phương trình (2), ta có:

3x + 5y = 3 . 0 + 5 . 2 = 0 + 10 = 10 ≠ –3 nên (0; 2) không phải là nghiệm của phương trình (2).

• Thay x = 4; y = –3 vào phương trình (2), ta có:

3x + 5y = 3 . 4 + 5 . (–3) = 12 – 15 = –3 nên (4; –3) là nghiệm của phương trình (2).

Ta thấy nghiệm chung của phương trình (1) và phương trình (2) là cặp số (4; –3).

Do đó, cặp số (4; –3) là nghiệm của hệ gồm phương trình (1) và phương trình (2).

c) Đường thẳng 5x + 4y = 8 đi qua điểm A(0; 2) và B(4; –3).

Đường thẳng 3x + 5y = –3 đi qua điểm B(4; –3) và C(–1; 0).

Hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 cắt nhau tại B(4; –3), tức là (4; –3) là nghiệm của hệ (1) và (2).

Sachbaitap.com