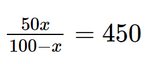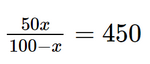Giải bài 2.12, 2.13, 2.14, 2.15 trang 36 SGK Toán 9 Kết nối tri thức tập 1

Bài 2.12 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức

Giải các phương trình sau:

a) \(2\left( {x + 1} \right) = \left( {5x - 1} \right)\left( {x + 1} \right);\)

b) \(\left( { - 4x + 3x} \right)x = \left( {2x + 5} \right)x.\)

Phương pháp:

Chú ý cần đưa phương trình đã cho về phương trình dạng \(A\left( x \right).B\left( x \right) = 0\) thì \(A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)

Lời giải:

a) 2(x + 1) = (5x – 1)(x + 1)

2(x + 1) – (5x – 1)(x + 1) = 0

(x + 1)(2 – 5x + 1) = 0

(x + 1)(3 – 5x) = 0

x + 1 = 0 hoặc 3 – 5x = 0

x = –1 hoặc 5x = 3

b) (–4x + 3)x = (2x + 5)x

(–4x + 3)x – (2x + 5)x = 0

x(–4x + 3 – 2x – 5) = 0

x(–6x – 2) = 0

x = 0 hoặc –6x – 2 = 0

x = 0 hoặc –6x = 2

Bài 2.13 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức

Để loại bỏ x% một loại tảo độc khỏi một hồ nước, người ta ước tính chi phí cần bỏ ra là

\(C\left( x \right) = \frac{{50x}}{{100 - x}}\) (triệu đồng), với \(0 \le x < 100.\)

Nếu bỏ ra 450 triệu đồng, người ta có thể lọai bỏ được bao nhiêu phần trăm loại tảo độc đó?

Phương pháp:

Chi phí bỏ ra là 450 triệu đồng nên ta có \(C\left( x \right) = 450\) từ đó ta có phương trình chứa ẩn ở mẫu, ta giải phương trình đối chiếu điều kiện rồi kết luận bài toán.

Lời giải:

Theo bài, chi phí để loại bỏ tảo độc là C = 450 triệu đồng, nên ta có phương trình: 

Giải phương trình:

50x = 450.(100 – x)

50x = 45 000 – 450x

50x + 450x  = 45 000

500x = 45 000

x = 90.

Giá trị x = 90 thỏa mãn điều kiện 0 ≤ x < 100.

Vậy nếu bỏ ra 450 triệu đồng, người ta có thể loại bỏ được 90% loại tảo độc đó.

Bài 2.14 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức

Giải các phương trình sau:

a) \(\frac{1}{{x + 2}} - \frac{2}{{{x^2} - 2x + 4}} = \frac{{x - 4}}{{{x^3} + 8}};\)

b) \(\frac{{2x}}{{x - 4}} + \frac{3}{{x + 4}} = \frac{{x - 12}}{{{x^2} - 16}}.\)

Phương pháp:

Các bước giải phương trình chứa ẩn ở mẫu

-  Bước 1: Tìm ĐKXĐ

-  Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu

-  Bước 3: Giải phương trình vừa thu được

-  Bước 4: Kết luận (đối chiếu ĐKXĐ).

Lời giải:

Suy ra x² – 4x = x – 4. (*)

Giải phương trình (*):

x² – 4x = x – 4

x(x – 4) – (x – 4) = 0

(x – 4)(x – 1) = 0

x – 4 = 0 hoặc x – 1 = 0

x = 4 (thỏa mãn ĐKXĐ) hoặc x = 1 (thỏa mãn ĐKXĐ).

Vậy phương trình đã cho có nghiệm là x = 4 và x = 1.

Suy ra 2x² + 11x – 12 = x – 12. (*)

Giải phương trình (*):

2x² + 11x – 12 = x – 12

2x² + 11x – 12 – x + 12 = 0

2x² + 10x = 0

2x(x + 5) = 0

2x = 0 hoặc x + 5 = 0

x = 0 (thỏa mãn ĐKXĐ) hoặc x = –5 (thỏa mãn ĐKXĐ).

Vậy phương trình đã cho có nghiệm là x = 0 và x = –5.

Bài 2.15 trang 37 SGK Toán 9 tập 1 - Kết nối tri thức

Cho \(a > b,\) chứng minh rằng:

a) \(4a + 4 > 4b + 3;\)

b) \(1 - 3a < 3 - 3b.\)

Phương pháp:

Áp dụng quy tắc:

-  Cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều với bất đẳng thức đã cho;

-  Nhân cả hai vế của bất đẳng thức với cùng 1 số dương ta được một bất đẳng thức cùng chiều với bất đẳng thức đã cho;

-  Nhân cả hai vế của bất đẳng thức với một số âm thì ta được một bất đẳng thức ngược chiều với bất đẳng thức đã cho.

-  Áp dụng tính chất bắc cầu \(a < b;b < c\) thì \(a < c\)

Lời giải:

a) Vì a > b nên 4a > 4b, suy ra 4a + 3 > 4b + 3.

Mà 4a + 4 > 4a + 3 nên 4a + 4 > 4b + 3.

Vậy 4a + 4 > 4b + 3.

b) Vì a > b nên –3a < –3b, suy ra 3 – 3a < 3 – 3b.

Mà 1 – 3a < 3 – 3a nên 1 – 3a < 3 – 3b.

Vậy 1 – 3a < 3 – 3b.

Sachbaitap.com