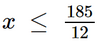Giải bài 2.16, 2.17, 2.18, 2.19, 2.20 trang 41 SGK Toán 9 Kết nối tri thức tập 1

Bài 2.16 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức

Giải các bất phương trình sau:

a) \(x - 5 \ge 0;\)

b) \(x + 5 \le 0;\)

c) \( - 2x - 6 > 0;\)

d) \(4x - 12 < 0.\)

Phương pháp:

Bất phương trình bậc nhất một ẩn \(ax + b < 0\left( {a \ne 0} \right)\) được giải như sau:

\(\begin{array}{l}ax + b < 0\\ax <  - b.\end{array}\)

Nếu \(a > 0\) thì \(x < \frac{{ - b}}{a}.\)

Nếu \(a < 0\) thì \(x > \frac{{ - b}}{a}.\)

Các bất phương trình \(ax + b > 0;ax + b \le 0;ax + b \ge 0\) giải tương tự.

Lời giải:

a) x – 5 ≥ 0

x ≥ 5.

Vậy nghiệm của bất phương trình đã cho là x ≥ 5.

b) x + 5 ≤ 0

x ≤ –5.

Vậy nghiệm của bất phương trình đã cho là x ≤ –5.

c) –2x – 6 > 0

–2x > 6

x < –3.

Vậy nghiệm của bất phương trình đã cho là x < –3.

d) 4x – 12 < 0

4x < 12

x < 3.

Vậy nghiệm của bất phương trình đã cho là x < 3.

Bài 2.17 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức

Giải các bất phương trình sau:

a) \(3x + 2 > 2x + 3;\)

b) \(5x + 4 <  - 3x - 2.\)

Phương pháp:

Cần đưa các phương trình đã cho về dạng bất phương trình bậc nhất một ẩn(thông qua tính chất của bất đẳng thức đối với phép cộng và phép nhân, rồi giải như sau

\(\begin{array}{l}ax + b < 0\\ax <  - b.\end{array}\)

Nếu \(a > 0\) thì \(x < \frac{{ - b}}{a}.\)

Nếu \(a < 0\) thì \(x > \frac{{ - b}}{a}.\)

Các bất phương trình \(ax + b > 0;ax + b \le 0;ax + b \ge 0\) giải tương tự.

Lời giải:

a) 3x + 2 > 2x + 3

3x – 2x > 3 – 2

x > 1.

Vậy nghiệm của bất phương trình đã cho là x > 1.

b) 5x + 4 < –3x – 2.

5x + 3x < – 2 – 4

8x < –6

Bài 2.18 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức

Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 1 tháng là 0,4%. Hỏi nếu muốn có số tiền lãi hàng tháng ít nhất là 3 triệu đồng thì số tiền gửi lãi tiết kiệm ít nhất là bao nhiêu (làm tròn đến triệu đồng)?

Phương pháp:

Chú ý: Số tiền lãi = Tiền gửi nhân lãi suất

Từ đó ta lập được bất phương trình, giải bất phương trình ta được kết quả của bài toán.

Lời giải:

Gọi x (triệu đồng) là số tiền gửi tiết kiệm (x > 0).

Khi đó số tiền lãi 1 tháng là 0,4%.x = 0,004x (triệu đồng).

Để số tiền lãi hàng tháng ít nhất là 3 triệu đồng thì ta phải có:

0,004x ≥ 3

x ≥ 750.

Vậy số tiền tiết kiệm ít nhất là 750 triệu đồng để có số tiền lãi hàng tháng ít nhất là 3 triệu đồng.

Bài 2.19 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức

Một hãng taxi có giá mở cửa là 15 nghìn đồng và giá 12 nghìn đồng cho mỗi kilomet tiếp theo. Hỏi với 200 nghìn đồng thì hành khách có thể di chuyển được tối đa bao nhiêu kilomet (làm tròn đến hàng đơn vị)?

Phương pháp:

Chú ý: Số tiền đi taxi = tiền mở cửa + tiền di chuyển ( số km nhân 12 nghìn đồng). Và số tiền di chuyển của hành khách là  200 nghìn đồng. Từ đó ta có bất phương trình. Giải bất phương trình ta được kết quả của bài toán.

Lời giải:

Gọi x là số kilômét mà hành khách đó có thể di chuyển với 200 nghìn đồng (x > 0).

Giá tiền cho x km là 12x (nghìn đồng).

Giá mở cửa của taxi là 15 nghìn đồng nên số tiền cần thanh toán khi đi x km là: 15 + 12x (nghìn đồng).

Theo bài, ta có:

15 + 12x ≤ 200

12x ≤ 185

Mà x > 0 và làm tròn đến hàng đơn vị nên với 200 nghìn đồng thì hành khách có thể di chuyển được tối đa 15 kilômét.

Bài 2.20 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức

Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại 180 ml nặng trung bình 10 kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5,25 tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng 65 kg?

Phương pháp:

Chú ý: Khối lượng xe có thể chở = khối lượng của các thùng bia (khối lượng 1 thùng nhân với số thùng) + khối lượng bác lái xe. Trọng tải là 5,25 tấn nên khối lượng xe có thể chở luôn nhỏ hơn hoặc bằng trọng tải.

Lời giải:

Đổi đơn vị: 5,25 tấn = 5 250 kg.

Gọi x (thùng) là số sữa mà xe có thể chở (x ∈ ℕ*).

Khi đó, khối lượng sữa mà xe chở là: 10x (kg).

Tổng khối lượng sữa và bác tài xế là: 65 + 10x (kg).

Do trọng tải (tổng khối lượng tối đa cho phép mà xe có thể chở) là 5 250 kg nên ta có:

65 + 10x ≤ 5 250

10x ≤ 5 185

x ≤ 518,5.

Mà x ∈ ℕ* nên xe tải đó có thể chở tối đa 518 thùng sữa.

Sachbaitap.com