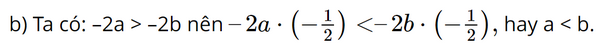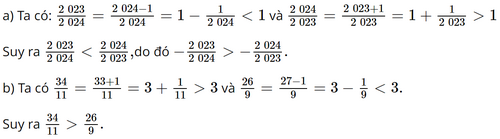Giải bài 2.6, 2.7, 2.8, 2.9, 2.11, 2.12 trang 35 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 35 Kết nối tri thức tập 1. Bài 2.6: Dùng kí hiệu để viết bất đẳng thức tương ứng trong mỗi trường hợp sau: a) x nhỏ hơn hoặc bằng -2;. Bài 2.7: Viết một bất đẳng thức phù hợp trong mỗi trường hợp sau: a) Bạn phải ít nhất 18 tuổi mới được phép lái ô tô; Bài 2.6 trang 35 SGK Toán 9 tập 1 - Kết nối tri thức Dùng kí hiệu để viết bất đẳng thức tương ứng trong mỗi trường hợp sau: a) x nhỏ hơn hoặc bằng -2; b) m là số âm; c) y là số dương; d) p lớn hơn hoặc bằng 2 024. Phương pháp: Trên tập số thực, với hai số a và b có ba trường hợp: - Số a lớn hơn số b, kí hiệu \(a > b.\) - Số a bé hơn số b, kí hiệu \(a < b.\) - Số a bằng số b, kí hiệu \(a = b.\) Lời giải: a) x ≤ –2; b) m < 0; c) y > 0; d) p ≥ 2 024. Bài 2.7 trang 35 SGK Toán 9 tập 1 - Kết nối tri thức Viết một bất đẳng thức phù hợp trong mỗi trường hợp sau: a) Bạn phải ít nhất 18 tuổi mới được phép lái ô tô; b) Xe buýt chở được tối đa 45 người; c) Mức lương tối thiểu cho một giờ làm việc của người lao động là 20 000 đồng. Phương pháp: a) Bạn phải ít nhất 18 tuổi mới được phép lái ô tô tức là số tuổi của bạn phải lớn hơn hoặt bằng 18 tuổi thì mới được lái ô tô b) Xe buýt chở được tối đa 45 người tức là số người trên xe buýt nhỏ hơn hoặc bằng 45 người. c) Mức lương tối thiểu cho một giờ làm việc của người lao động là 20 000 đồng tức là mức lương tối thiểu của một giờ làm việc của người lao động sẽ lớn hơn hoặc bằng 20 000 đồng. Lời giải: a) Gọi x (tuổi) là số tuổi của bạn, khi đó bất đẳng thức phù hợp cho “Bạn phải ít nhất 18 tuổi mới được phép lái ô tô” là x ≥ 18. b) Gọi y (người) là số người xe buýt có thể chở được, khi đó bất đẳng thức phù hợp cho “Xe buýt chở được tối đa 45 người” là y ≤ 45. c) Gọi z (đồng) là mức lương cho một giờ làm việc của người lao động, khi đó bất đẳng thức phù hợp cho “Mức lương tối thiểu cho một giờ làm việc của người lao động là 20 000 đồng” là z ≥ 20 000. Bài 2.8 trang 35 SGK Toán 9 tập 1 - Kết nối tri thức Không thực hiện phép tính, hãy chứng minh: a) \(2.\left( { - 7} \right) + 2023 < 2.\left( { - 1} \right) + 2023;\) b) \(\left( { - 3} \right).\left( { - 8} \right) + 1975 > \left( { - 3} \right).\left( { - 7} \right) + 1975.\) Phương pháp: Áp dụng quy tắc: - Cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều với bất đẳng thức đã cho; - Nhân cả hai vế của bất đẳng thức với cùng 1 số dương ta được một bất đẳng thức cùng chiều với bất đẳng thức đã cho; - Nhân cả hai vế của bất đẳng thức với một số âm thì ta được một bất đẳng thức ngược chiều với bất đẳng thức đã cho. Lời giải: a) Vì –7 < –1 nên 2 . (–7) < 2 . (–1) Do đó 2 . (–7) + 2 023 < 2 . (–1) + 2 023. b) Vì –8 < –7 nên (–3) . (–8) > (–3) . (–7) Do đó (–3) . (–8) + 1 975 > (–3) . (–7) + 1 975. Bài 2.9 trang 35 SGK Toán 9 tập 1 - Kết nối tri thức Cho \(a < b,\) hãy so sánh: a) \(5a + 7\) và \(5b + 7;\) b) \( - 3a - 9\) và \( - 3b - 9.\) Phương pháp: Áp dụng quy tắc: - Cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều với bất đẳng thức đã cho; - Nhân cả hai vế của bất đẳng thức với cùng 1 số dương ta được một bất đẳng thức cùng chiều với bất đẳng thức đã cho; - Nhân cả hai vế của bất đẳng thức với một số âm thì ta được một bất đẳng thức ngược chiều với bất đẳng thức đã cho. Lời giải: a) Vì a < b nên 5a < 5b, suy ra 5a + 7 < 5b + 7. Vậy 5a + 7 < 5b + 7. b) Vì a < b nên –3a > –3b, suy ra –3a – 9 > –3b – 9. Vậy –3a – 9 > –3b – 9. Bài 2.10 trang 35 SGK Toán 9 tập 1 - Kết nối tri thức So sánh hai số a và b, nếu: a) \(a + 1954 < b + 1954;\) b) \( - 2a > - 2b.\) Phương pháp: Áp dụng quy tắc: - Cộng cả hai vế của bất đẳng thức với một số ta được bất đẳng thức cùng chiều với bất đẳng thức đã cho; - Nhân cả hai vế của bất đẳng thức với cùng 1 số dương ta được một bất đẳng thức cùng chiều với bất đẳng thức đã cho; - Nhân cả hai vế của bất đẳng thức với một số âm thì ta được một bất đẳng thức ngược chiều với bất đẳng thức đã cho. Lời giải: a) Ta có: a + 1 954 < b + 1 954 Suy ra: a + 1 954 – 1 954 < b + 1 954 – 1 954 hay a < b. Vậy a < b.
Vậy a < b. Bài 2.11 trang 35 SGK Toán 9 tập 1 - Kết nối tri thức Chứng minh rằng: a) \( - \frac{{2023}}{{2024}} > - \frac{{2024}}{{2023}};\) b) \(\frac{{34}}{{11}} > \frac{{26}}{9}.\) Phương pháp: Sử dụng tính chất bắc cầu: Nếu \(a < b\) và \(b < c\) thì \(a < c.\) Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài 5: Bất đẳng thức và tính chất
|
-

Giải bài 2.12, 2.13, 2.14, 2.15 trang 36 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 36 Kết nối tri thức tập 1. Bài 2.12: Giải các phương trình sau. Bài 2.13: Để loại bỏ x% một loại tảo độc khỏi một hồ nước, người ta ước tính chi phí cần bỏ ra là

 Tải ngay
Tải ngay