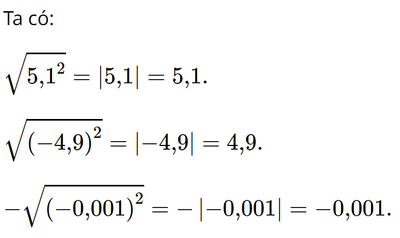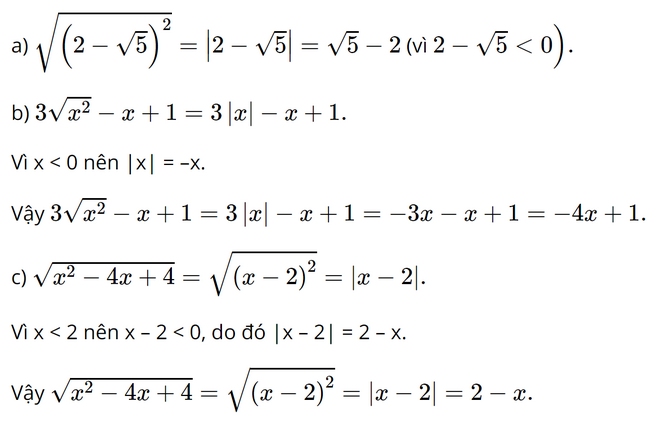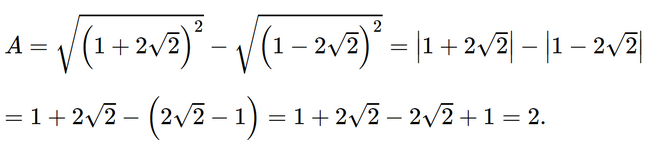Giải bài 3.1, 3.2, 3.3, 3.4, 3.5, 3.6 trang 48 SGK Toán 9 Kết nối tri thức tập 1

Bài 3.1 trang 48 SGK Toán 9 tập 1 - Kết nối tri thức

Tìm căn bậc hai của mỗi số sau (làm tròn đến chữ số thập phân thứ hai) :

a) 24,5;

b) \(\frac{9}{{10}}.\)

Phương pháp:

- Sử dụng MTCT ta có \(\sqrt {24,5}  = 4,949747468\) nên \(\sqrt {24,5}  \approx 4,95\)

- Sử dụng MTCT ta có \(\sqrt {\frac{9}{{10}}}  = 0,9486832981\) nên \(\sqrt {\frac{9}{{10}}}  \approx 0,95\)

Lời giải:

Sử dụng MTCT:

Bài 3.2 trang 48 SGK Toán 9 tập 1 - Kết nối tri thức

Để chuẩn bị trồng cây trên vỉa hè, người ta để lại những ô đất hình tròn có diện tích khoảng \(2\,{m^2}.\) Em hãy ước lượng (với độ chính xác 0,005) đường kính của các ô đất đó khoảng bao nhiêu mét?

Phương pháp:

Diện tích của hình tròn là \(C = 3,14{R^2}\) từ đó ta có công thức tính bán kính \(R = \sqrt {\frac{C}{\pi }} \)

Lời giải:

Công thức tính diện tích hình tròn bán kính R là S = πR².

Vậy ta ước lượng được đường kính của các ô đất đó khoảng 1,60 m.

Bài 3.3 trang 48 SGK Toán 9 tập 1 - Kết nối tri thức

Tìm điều kiện xác định của \(\sqrt {x + 10} \) và tính giá trị của căn thức tại \(x =  - 1.\)

Phương pháp:

Ta có \(\sqrt {{A^2}}  = \left| A \right|\)

Lời giải:

Bài 3.4 trang 48 SGK Toán 9 tập 1 - Kết nối tri thức

Tính: \(\sqrt {5,{1^2}} ;\sqrt {{{\left( { - 4,9} \right)}^2}} ; - \sqrt {{{\left( { - 0,001} \right)}^2}} .\)

Phương pháp:

Chú ý: Số tiền đi taxi = tiền mở cửa + tiền di chuyển ( số km nhân 12 nghìn đồng). Và số tiền di chuyển của hành khách là  200 nghìn đồng. Từ đó ta có bất phương trình. Giải bất phương trình ta được kết quả của bài toán.

Lời giải:

Bài 3.5 trang 48 SGK Toán 9 tập 1 - Kết nối tri thức

Rút gọn các biểu thức sau:

a) \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} ;\)

b) \(3\sqrt {{x^2}}  - x + 1\left( {x < 0} \right);\)

c) \(\sqrt {{x^2} - 4x + 4} \left( {x < 2} \right).\)

Phương pháp:

Sử dụng kiến thức \(\sqrt {{A^2}}  = \left| A \right|\)

Lời giải:

Bài 3.6 trang 48 SGK Toán 9 tập 1 - Kết nối tri thức

Không dùng MTCT, chứng tỏ biểu thức A có giá trị là số nguyên:

\(A = \sqrt {{{\left( {1 + 2\sqrt 2 } \right)}^2}}  - \sqrt {{{\left( {1 - 2\sqrt 2 } \right)}^2}} .\)

Phương pháp:

Chú ý: \(\sqrt {{A^2}}  = \left| A \right|\)và quy tắc dấu ngoặc (có dấu trừ trước ngoặc thì phá ngoặc đổi dấu các hạng tử trong ngoặc) 

Lời giải:

Ta có: 

Vậy giá trị của biểu thức A là số nguyên.

Sachbaitap.com