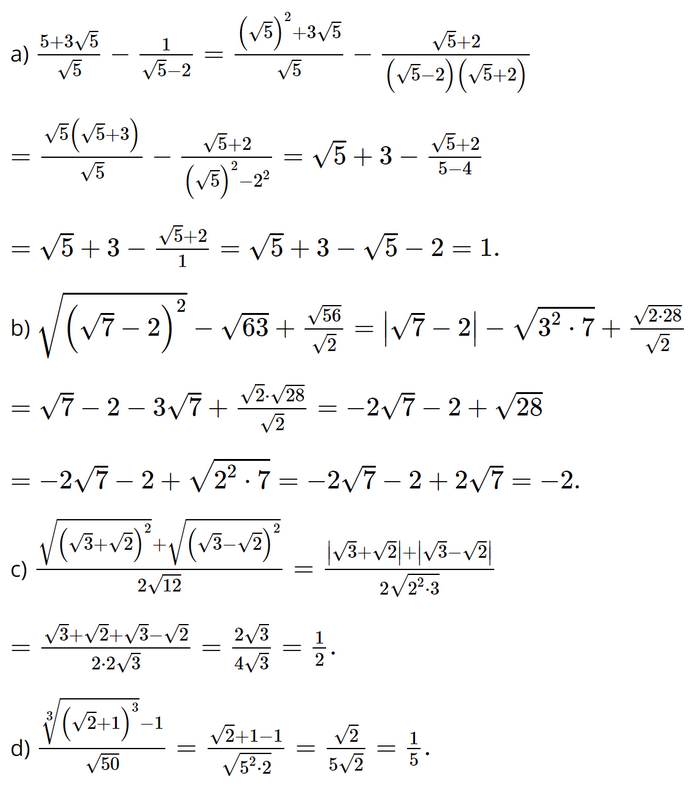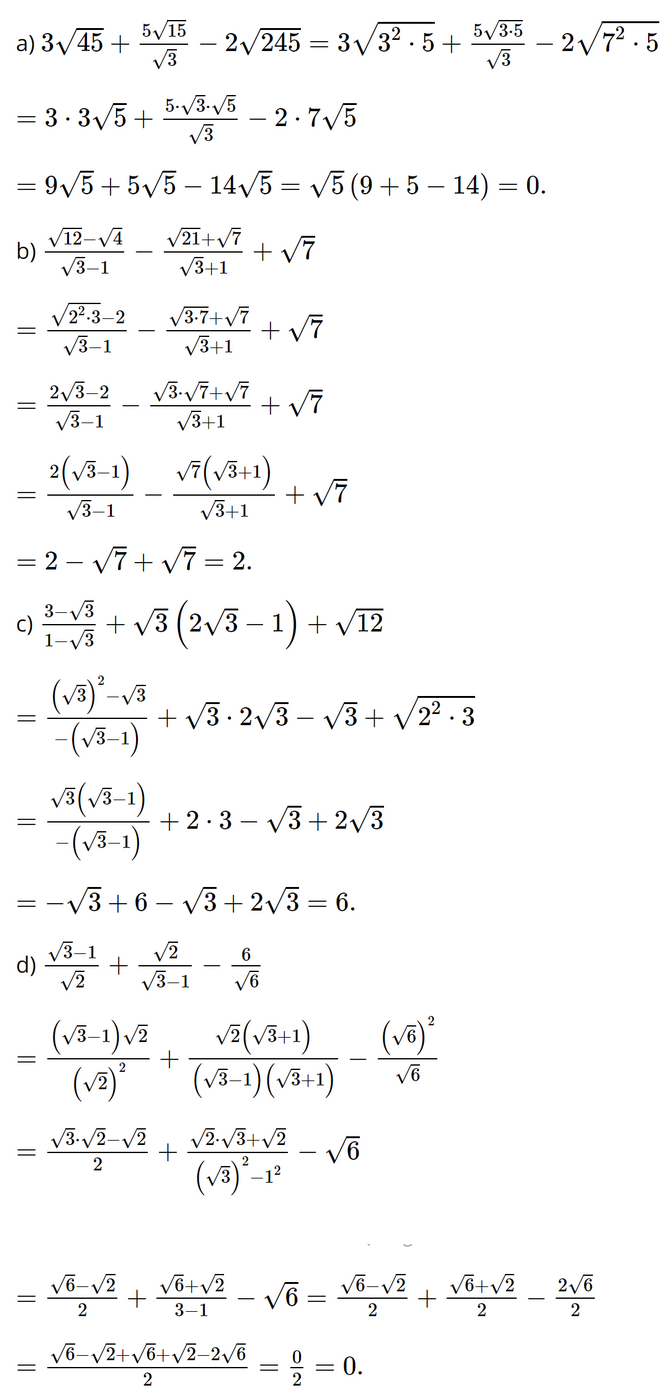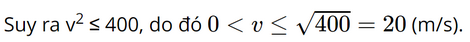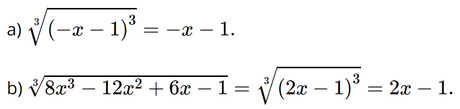Giải bài 3.28, 3.29, 3.30, 3.31 trang 64 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 64 Kết nối tri thức tập 1.Bài 3.25: Một người thợ muốn làm một thùng tôn hình lập phương có thể tích bằng (730,d{m^3}.) Em hãy ước lượng chiều dài cạnh thùng khoảng bao nhiêu dm? Bài 3.26: Rút gọn các biểu thức sau: Bài 3.28 trang 64 SGK Toán 9 tập 1 - Kết nối tri thức Rút gọn các biểu thức sau: a) \(\frac{{5 + 3\sqrt 5 }}{{\sqrt 5 }} - \frac{1}{{\sqrt 5 - 2}};\) b) \(\sqrt {{{\left( {\sqrt 7 - 2} \right)}^2}} - \sqrt {63} + \frac{{\sqrt {56} }}{{\sqrt 2 }};\) c) \(\frac{{\sqrt {{{\left( {\sqrt 3 + \sqrt 2 } \right)}^2}} + \sqrt {{{\left( {\sqrt 3 - \sqrt 2 } \right)}^2}} }}{{2\sqrt {12} }};\) d) \(\frac{{\sqrt[3]{{{{\left( {\sqrt 2 + 1} \right)}^3}}} - 1}}{{\sqrt {50} }}.\) Phương pháp: Sử dụng kết hợp các phương pháp trục căn thức, khai căn bặc hai, bậc ba, đưa thừa số ra ngoài dấu căn, rồi thu gọn biểu thức. Lời giải:
Bài 3.29 trang 64 SGK Toán 9 tập 1 - Kết nối tri thức Tính giá trị của các biểu thức sau: a) \(3\sqrt {45} + \frac{{5\sqrt {15} }}{{\sqrt 3 }} - 2\sqrt {245} ;\) b) \(\frac{{\sqrt {12} - \sqrt 4 }}{{\sqrt 3 - 1}} - \frac{{\sqrt {21} + \sqrt 7 }}{{\sqrt 3 + 1}} + \sqrt 7 ;\) c) \(\frac{{3 - \sqrt 3 }}{{1 - \sqrt 3 }} + \sqrt 3 \left( {2\sqrt 3 - 1} \right) + \sqrt {12} ;\) d) \(\frac{{\sqrt 3 - 1}}{{\sqrt 2 }} + \frac{{\sqrt 2 }}{{\sqrt 3 - 1}} - \frac{6}{{\sqrt 6 }}.\) Phương pháp: Sử dụng kết hợp các phương pháp trục căn thức, khai căn bặc hai, bậc ba, đưa thừa số ra ngoài dấu căn, rồi thu gọn biểu thức. Chú ý biểu thức nào rút gọn được luôn, ta rút gọn trước khi làm các phương pháp trên. Lời giải:
Bài 3.30 trang 64 SGK Toán 9 tập 1 - Kết nối tri thức Giả sử lực F của gió khi thổi theo phương vuông góc với bề mặt cánh buồm của một con thuyền tỉ lệ thuận với bình phương tốc độ của gió, hệ số tỉ lệ là 30. Trong đó, lực F được tính bằng N (Newton) và tốc độ được tính bằng m/s. a) Khi tốc độ của gió là 10 m/s thì lực F bằng bao nhiêu Newton? b) Nếu cánh buồm chỉ có thể chịu được một áp lực tối đa là 12000 N thì con thuyền đó có thể đi được trong gió với tốc độ gió tối đa là bao nhiêu? Phương pháp: Ta có lực F tỉ lệ thuận với bình phương tốc độ của gió theo tỉ lệ là 30 nên ta có lực F = bình phương tốc độ gió nhân 30. Lời giải: Gọi tốc độ của gió và v (m/s). Do F của gió khi thổi theo phương vuông góc với bề mặt cánh buồm của một con thuyền tỉ lệ thuận với bình phương tốc độ của gió, hệ số tỉ lệ là 30 nên ta có F = 30v2 (N). a) Khi v = 10 m/s thì ta có: F = 30.102 = 3 000 (N). b) Nếu F ≤ 12 000 N thì 30v2 ≤ 12 000
Bài 3.31 trang 62 SGK Toán 9 tập 1 - Kết nối tri thức Rút gọn các biểu thức sau: a) \(\sqrt[3]{{{{\left( { - x - 1} \right)}^3}}};\) b) \(\sqrt[3]{{8{x^3} - 12{x^2} + 6x - 1}}.\) Phương pháp: Sử dụng \(\sqrt[3]{{{A^3}}} = A\) và hằng đẳng thức \({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\) Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Luyện tập chung trang 63
|
-

Giải bài 3.32, 3.33, 3.34, 3.35, 3.36, 3.37, 3.38, 3.39 trang 65 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 65 Kết nối tri thức tập 1. Bài 3.35: Độ dài đường kính (mét) của hình tròn có diện tích (4,{m^2}) sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng A. 2,26. Bài 3.36: Một vật rơi tự do từ độ cao 396,9 m. Biết quãng đường chuyển động S (mét) của vật phụ thuộc vào thời gian t (giây) bởi công thức (S = 4,9{t^2}.) Vật chạm đất sau A. 8 giây.

 Tải ngay
Tải ngay