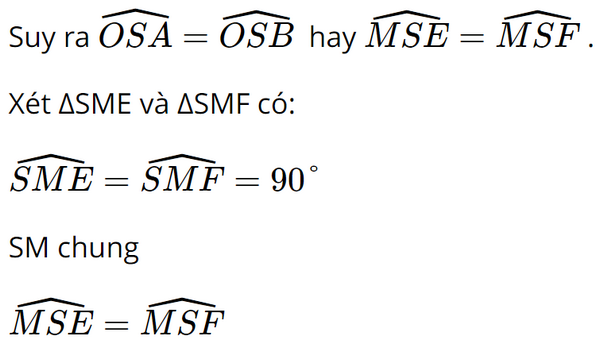Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1Giải SGK Toán 9 trang 103 Kết nối tri thức tập 1. Bài 5.21: Chứng minh đường thẳng đi qua A là và song song với BC là tiếp tuyến tức là đường thẳng đó vuông góc với bán kính (hoặc đường kính) tại điểm A. Bài 5.20 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a? Phương pháp: So sánh bán kính của mỗi hình tròn với khoảng cách giữa 2 đường thẳng, nếu hình tròn có bán kính lớn hơn thì nó đè lên đường thẳng a, ngược lại thì hình tròn không đè lên đường thẳng a. Lời giải:
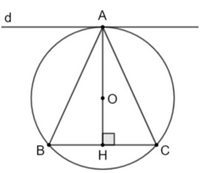
Vì a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm nên đường thẳng a tiếp xúc với hình tròn bán kính 6 cm, hay hình tròn bán kính 6 cm đè lên đường thẳng a. Vì 4 cm < 6 cm nên đường thẳng a và hình tròn bán kính 4 cm không cắt nhau, hay hình tròn bán kính 4 cm không đè lên trường thẳng a. Vì 7 cm > 6 cm; 8 cm > 6 cm nên đường thẳng a và hình tròn bán kính 4 cm cắt nhau, hay hình tròn bán kính 7 cm và 8 cm đè lên đường thẳng a. Vậy hình tròn bán kính 4 cm không đè lên trường thẳng a, hình tròn bán kính 6 cm, 7 cm và 8 cm đè lên đường thẳng a. Bài 5.21 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức Chứng minh đường thẳng đi qua A là và song song với BC là tiếp tuyến tức là đường thẳng đó vuông góc với bán kính (hoặc đường kính) tại điểm A. Phương pháp: Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O). Lời giải:
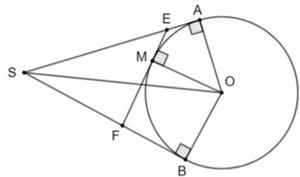
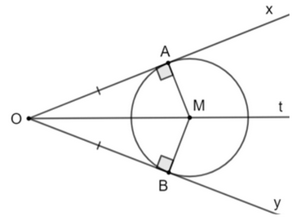
Ta có đường thẳng AO là trục đối xứng của đường tròn. Nên B là điểm đối xứng của C qua AO. Gọi H là giao điểm của AO và BC. Khi đó ta có: AH ⊥ BC mà d // BC nên AH ⊥ d. Vậy d là một tiếp tuyến của đường tròn. Bài 5.22 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại P. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (P; PA). Phương pháp: Ta có: OA là tiếp tuyến của đường tròn (P; PA) do OA \( \bot \) PA tại A. Xét cặp tam giác OAP và tam giác OBP, từ đó suy ra PA = PB và OB \( \bot \) PB. Hay OB là tiếp tuyến của đường tròn (P; PA). Lời giải:
Xét ΔOAM và ΔOBM có: OM chung
OA = OB Do đó ΔOAM = ΔOBM (c.g.c). Suy ra AM = BM (hai cạnh tương ứng).
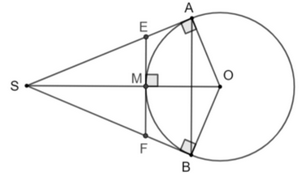
Do đó OA là tiếp tuyến của đường tròn (M; MA). Vậy OA và OB là hai tiếp tuyến cắt nhau của (O). Bài 5.23 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F. a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB. b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF. Phương pháp: Áp dụng tính chất của hai tiếp tuyến cắt nhau. Lời giải: a)
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA. Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB. Chu vi tam giác SEF là: CSEF = SE + SF + EF = SE + SF + EM + MF = SE + EA + SF + BF = SA + SB. Vậy chu vi của tam giác SEF bằng SA + SB. b)
Vì SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của .
Do đó ΔSME = ΔSMF (g.c.g) Suy ra SE = SF (hai cạnh tương ứng). Sachbaitap.com
Xem thêm tại đây:
Bài 16: Vị trí tương đối của đường thẳng và đường tròn
|
-

Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 107 Kết nối tri thức tập 1.Bài 5.24: Hình 5.37 cho thấy hình ảnh của những đường tròn qua cách trình bày một số sản phẩm mây tre đan. Bằng cách đánh số các đường tròn, em hãy chỉ ra một vài cặp đường tròn cắt nhau và cặp đường tròn không giao nhau.

 Tải ngay
Tải ngay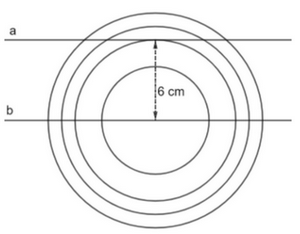

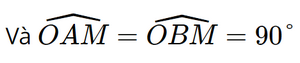 (hai góc tương ứng) hay OB ⊥ MB.
(hai góc tương ứng) hay OB ⊥ MB.