Giải bài 9.11, 9.12, 9.13, 9.14, 9.15, 9.15 trang 92 SGK Toán 8 Kết nối tri thức tập 2Giải sách giáo khoa Toán lớp 8 trang 92 Kết nối tri thức với cuộc sống tập 2: bài 9.11, 9.12, 9.13, 9.14, 9.15, 9.15. Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C' Bài 9.11 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức Cho ΔABC ∽ ΔDEF. Biết \(\widehat A = {60^o};\widehat E = {80^o}\), hãy tính số đo các góc \(\widehat B,\widehat C,\widehat D,\widehat F\) Phương pháp: - Sử dụng ΔABC ∽ ΔDEF suy ra \(\widehat A = \widehat D{,^{}}\widehat B = \widehat E{,^{}}\widehat C = \widehat F\). - Từ đó tính các góc \(\widehat B,\widehat C,\widehat D,\widehat F\) Lời giải: Vì ΔABC ∽ ΔDEF. Suy ra Mà Có Bài 9.12 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C' Phương pháp: - Từ ΔABC ∽ ΔA'B'C' tính được tỉ số đồng dạng. Suy ra chu vi tam giác A’B’C’. Lời giải: Vì ΔABC ∽ ΔA'B'C' nên Suy ra A'B' + A'C' + B'C' = 2(AB + AC + BC) = 2 . 10 = 20 (cm). Vậy chu vi tam giác A'B'C' là 20 cm. Bài 9.13 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\) a) Chứng minh rằng ΔABD ∽ ΔBDC b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC
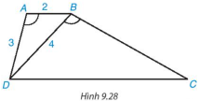
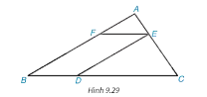
Phương pháp: a) Chứng minh ΔABD ∽ ΔBDC (g.g) b) Tính tỉ số đồng dạng của tam giác ABD và tam giác BDC. Từ đó tính độ dài của DC, BC Lời giải: a) Vì AB // CD (giả thiết) nên + Xét ΔABD và ΔBDC có: Suy ra ΔABD ∽ ΔBDC (g.g). b) Ta có: Vậy ΔABD ∽ ΔBDC với tỉ số đồng dạng Suy ra Suy ra BC = 2 . 3 = 6 cm; DC = 4 . 2 = 8 cm. Bài 9.14 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE=4cm, AB=6cm. Chứng minh rằng ΔAEF ∽ ΔECD và tính tỉ số đồng dạng
Phương pháp: Áp dụng tính chất hai đường thẳng song song => Các cặp góc bằng nhau => Hai tam giác đồng dạng, ta có tỉ số đồng dạng Lời giải: - Có EF // BC. Suy ra - Có EF // BD (vì EF // BC) và DE // FB (vì ED // AB). Suy ra EFBD là hình bình hành. Suy ra
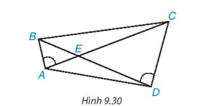
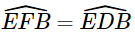 . .Mà Do đó, Từ (1) và (2) suy ra ΔAEF ∽ ΔECD (g.g). Vì EFBD là hình bình hành nên BF = ED = 4 cm. Mà AF + BF = AB nên AF = AB – BF = 6 – 4 = 2 Khi đó, Vậy ΔAEF ∽ ΔECD với tỉ số đồng dạng là Bài 9.15 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat {BAC} = \widehat {C{\rm{D}}B}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Phương pháp: - Chứng minh\(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\) - Chứng minh ΔAED ∽ ΔBEC (c.g.c) Lời giải: Xét ΔAEB và ΔDEC có:
Suy ra ΔAEB ∽ ΔDEC (g.g). Suy ra Xét ΔAED và ΔBEC có:
Suy ra ΔAED ∽ ΔBEC (c.g.c). Bài 9.16 trang 92 SGK Toán 8 tập 2 - Kết nối tri thức Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM=MD, 2BN=NC. Biết AB=5cm,CD=6cm. Hãy tính độ dài đoạn thẳng MN Phương pháp: Gọi I là giao điểm của AC và MN Sử dụng các tam giác đồng dạng để tính độ dài MI, IN. Từ đó tính độ dài đoạn MN. Lời giải:
Vẽ đường thẳng qua M song song với CD cắt AC tại E. Khi đó: Do đó
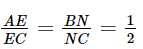 (2BN = NC), suy ra NE // AB (định lí Thalès đảo). (2BN = NC), suy ra NE // AB (định lí Thalès đảo).Ta có: ME // CD NE // AB AB // CD Do đó ME // CD và NE // CD, suy ra M, N, E thẳng hàng. Mặt khác ∆AME ∽ ∆ADC (vì ME // CD). Nên Tương tự ∆CEN ∽ ∆CAB (vì NE //AB) nên Vậy MN = ME + EN = Sachbaitap.com
Xem thêm tại đây:
Luyện tập chung (trang 91)
|
-

Giải bài 9.17, 9.18, 9.19, 9.20, 9.21, 9.22 trang 97 SGK Toán 8 Kết nối tri thức tập 2
Giải sách giáo khoa Toán lớp 8 trang 97 Kết nối tri thức với cuộc sống tập 2: bài 9.17, 9.18, 9.19, 9.20, 9.21, 9.22. Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông. Cho tam giác ABC cân tại đỉnh A, chiều cao AH=3cm và cạnh đáy BC=10cm. Hãy tính độ dài các cạnh bên AB, AC.

 Tải ngay
Tải ngay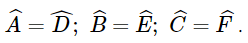
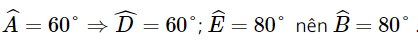
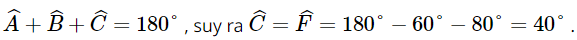
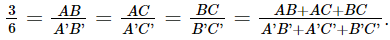
 (2 góc ở vị trí so le trong).
(2 góc ở vị trí so le trong).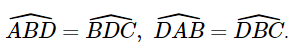 .
.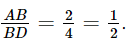 .
.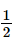 .
.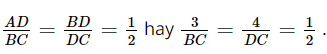 .
.
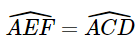 (2 góc đồng vị). (1)
(2 góc đồng vị). (1)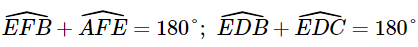 (kề bù).
(kề bù).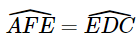 . (2)
. (2)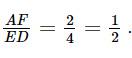
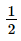
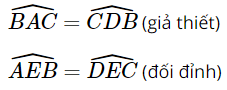
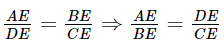
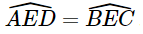 (2 góc đối đỉnh)
(2 góc đối đỉnh)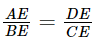 (chứng minh trên)
(chứng minh trên)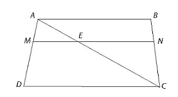
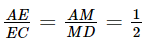 (định lí Thalès).
(định lí Thalès).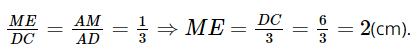
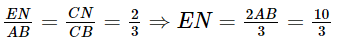 (cm).
(cm).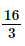 (cm).
(cm).