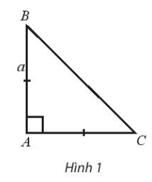
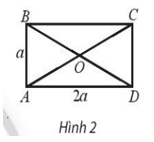
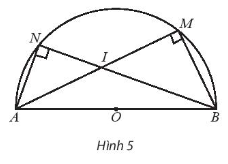
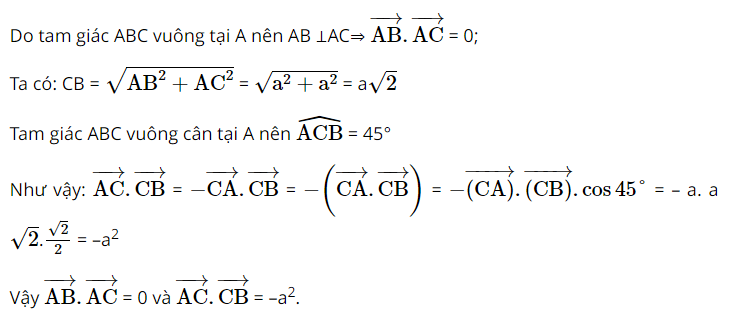Giải SBT Toán 10 trang 100, 101 Chân trời sáng tạo tập 1Giải bài 1, 2 trang 100, bài 3, 4, 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 5. Cho hai vectơ có độ dài lần lượt là 6 và 8 và có tích vô hướng là 24. Tính góc giữa hai vectơ đó. Bài 1 trang 100 SBT Toán 10 - Chân trời sáng tạo Cho tam giác vuông cân ABC có \(AB = AC = a\). Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} \) Lời giải: Bài 2 trang 100 SBT Toán 10 - Chân trời sáng tạo Cho hình chữ nhật ABCD có tâm O và cho \(AD = 2a,AB = a\). Tính: a) \(\overrightarrow {AB} .\overrightarrow {AO} \) b) \(\overrightarrow {AB} .\overrightarrow {AD} \) Phương pháp: Sử dụng công thức tính tích vô hướng \(\overrightarrow {{a_1}} .\overrightarrow {{a_2}} = \left| {\overrightarrow {{a_1}} } \right|.\left| {\overrightarrow {{a_2}} } \right|.\cos \left( {\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} } \right)\) Lời giải: Bài 3 trang 101 SBT Toán 10 - Chân trời sáng tạo Cho nửa đường tròn tâm O có đường kính \(AB = 2R\). Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như hình 5. a) Chứng minh: \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB} ;\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AB} .\overrightarrow {BA} \) b) Tính \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} \) theo R Lời giải: a) Ta có: \(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} = \left| {\overrightarrow {AI} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AI} ,\overrightarrow {AM} } \right)\\ = AI.AM.\cos 0^\circ = AI.AM\end{array}\) (*) Mặt khác \(AM = AB.\cos \widehat {MAB}\), thay vào (*) ta có: \(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} = AI.AM = AI.AB.\cos \widehat {MAB}\\ = \left| {\overrightarrow {AI} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AI} ,\overrightarrow {AB} } \right) = \overrightarrow {AI} .\overrightarrow {AB} \end{array}\) (đpcm) \(\begin{array}{l}\overrightarrow {BI} .\overrightarrow {BN} = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BN} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BN} } \right)\\ = BI.BN.\cos 0^\circ = BI.BN\end{array}\) (**) Mặt khác \(BN = BA.\cos \widehat {NBA}\), thay vào (**) ta có: \(\begin{array}{l}\overrightarrow {BI} .\overrightarrow {BN} = BI.BN = BI.BA.\cos \widehat {NBA}\\ = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BA} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BA} } \right) = \overrightarrow {BI} .\overrightarrow {BA} \end{array}\) (đpcm) b) Từ kết quả của câu a) ta có: \(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\\ = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {AB} .\overrightarrow {BI} = \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) = \overrightarrow {AB} \left( {\overrightarrow {AI} + \overrightarrow {IB} } \right) = {\overrightarrow {AB} ^2}\\ = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\end{array}\) Vậy \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = 4{R^2}\) Bài 4 trang 101 SBT Toán 10 - Chân trời sáng tạo Tính công sinh ra bởi một lực \(\overrightarrow F \) có độ lớn 60N kéo theo một vật di chuyển một vectơ \(\overrightarrow d \) có độ dài 200 m. Cho biết \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 60^\circ \) Lời giải: Ta có công thức tính công sinh ra bởi lực \(\overrightarrow F \) là \(A = \overrightarrow F \overrightarrow d = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) \Rightarrow A = 60.200.\cos 60^\circ = 6000\) Vậy độ lớn công sinh ra bởi lực \(\overrightarrow F \) là 6000 J Bài 5 trang 101 SBT Toán 10 - Chân trời sáng tạo Cho hai vectơ có độ dài lần lượt là 6 và 8 và có tích vô hướng là 24. Tính góc giữa hai vectơ đó. Lời giải: Ta có \(\overrightarrow {{a_1}} .\overrightarrow {{a_2}} = \left| {\overrightarrow {{a_1}} } \right|.\left| {\overrightarrow {{a_2}} } \right|.\cos \left( {\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} } \right)\\ \Rightarrow 24 = 6.8.\cos \left( {\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} } \right)\) \( \Rightarrow \cos \left( {\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} } \right) = \frac{1}{2} \\ \Rightarrow \left( {\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} } \right) = 60^\circ \) Sachbaitap.com
Xem thêm tại đây:
Bài 4. Tích vô hướng của hai vectơ - SBT Toán 10 CTST
|
-

Giải SBT Toán 10 trang 101, 102, 103 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, trang 101, bài 6, 7, 8, 9, 10 trang 102 bài 1, 2, 3 trang 102 bài 4, 5, 6, 7, 8, 9, 10, 11, 12 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1. Bài 3. Cho ba điểm phân biết A, B, C. Khằng định nào sau đây là đúng?

 Tải ngay
Tải ngay