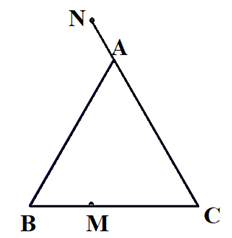
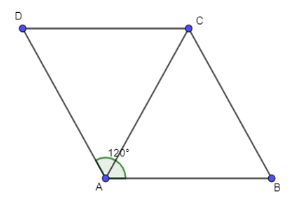
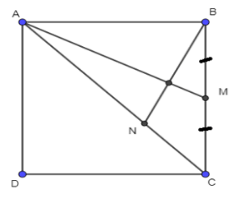
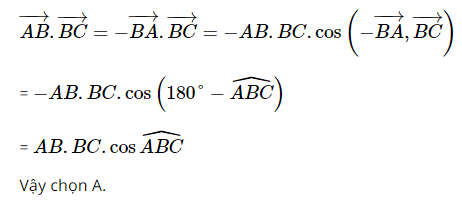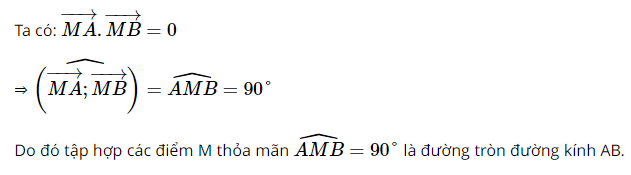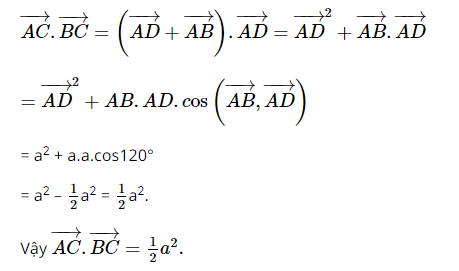Giải SBT Toán 10 trang 105, 106 Cánh Diều tập 1

Bài 57 trang 105 SBT Toán 10 - Cánh Diều

Cho tam giác ABC. Giá trị của biểu thức \(\overrightarrow {BA} .\overrightarrow {CA} \) bằng:

A. AB. AC. cos\(\widehat {BAC}\)   

B. – AB. AC. cos\(\widehat {BAC}\)            

C. AB. AC. cos\(\widehat {ABC}\)   

D. AB. AC. cos\(\widehat {ACB}\)

Lời giải:

Ta có: \(\overrightarrow {BA} .\overrightarrow {CA}  = \left( { - \overrightarrow {AB} } \right).\left( { - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.\cos \widehat {BAC}\)

Chọn A

Bài 58 trang 105 SBT Toán 10 - Cánh Diều

Cho tam giác ABC. Giá trị của biểu thức \(\overrightarrow {AB} .\overrightarrow {BC} \) bằng:

A. AB. BC. cos\(\widehat {ABC}\)   

B. AB. AC. cos\(\widehat {ABC}\)               

C. – AB. BC. cos\(\widehat {ABC}\)

D. AB. BC. cos\(\widehat {BAC}\)

Phương pháp:

Biến đổi \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) thành 2 vectơ chung gốc rồi sử dụng định nghĩa tích vô hướng của hai vectơ

Lời giải:

Đáp án đúng là A

Bài 59 trang 105 SBT Toán 10 - Cánh Diều

Cho đoạn thẳng AB. Tập hợp các điểm M nằm trong mặt phẳng thoả mãn \(\overrightarrow {MA} .\overrightarrow {MB}  = 0\)là:

A. Đường tròn tâm A bán kính AB                

B. Đường tròn tâm B bán kính AB                

C. Đường trung trực của đoạn thẳng AB       

D. Đường tròn đường kính AB

Phương pháp:

Sử dụng tính chất \(\overrightarrow a .\overrightarrow b  = 0 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {90^0}\) để tìm vị trí điểm M

Lời giải:

Đáp án đúng là D

Bài 60 trang 105 SBT Toán 10 - Cánh Diều

Nếu hai điểm M, N thoả mãn \(\overrightarrow {MN} .\overrightarrow {NM}  =  - 9\) thì:

A. MN = 9                  

B. MN = 3                  

C. MN = 81                

D. MN = 6

Lời giải:

Theo giả thiết, \(\overrightarrow {MN} .\overrightarrow {NM}  =  - 9 \Leftrightarrow \overrightarrow {MN} .\overrightarrow {MN}  = 9 \Leftrightarrow {\left( {\overrightarrow {MN} } \right)^2} = 9 \Leftrightarrow M{N^2} = 9 \Leftrightarrow MN = 3\) 

Chọn B

Bài 61 trang 105 SBT Toán 10 - Cánh Diều

Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thoả mãn \(BM = \frac{1}{3}BC,CN = \frac{5}{4}CA\). Tính:

a) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BN} \)

b) MN

Lời giải:

a) Ta có:

* \(\overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.\cos \widehat {BAC} = a.a.\cos {60^0} = \frac{{{a^2}}}{2}\)

* \(\overrightarrow {AM} .\overrightarrow {BN}  = \left( {\overrightarrow {CM}  - \overrightarrow {CA} } \right)\left( {\overrightarrow {CN}  - \overrightarrow {CB} } \right) = \overrightarrow {CM} .\overrightarrow {CN}  - \overrightarrow {CM} .\overrightarrow {CB}  - \overrightarrow {CA} .\overrightarrow {CN}  + \overrightarrow {CA} .\overrightarrow {CB} \)

Ta có: + \(\overrightarrow {CM} .\overrightarrow {CN}  = CM.CN.\cos \widehat {MCN} = \frac{{2a}}{3}.\frac{{5a}}{4}.\cos {60^0} = \frac{{5{a^2}}}{{12}}\)

           + \(\overrightarrow {CM} .\overrightarrow {CB}  = \frac{2}{3}\overrightarrow {CB} .\overrightarrow {CB}  = \frac{2}{3}B{C^2} = \frac{{2{a^2}}}{3}\)

           + \(\overrightarrow {CA} .\overrightarrow {CN}  = \overrightarrow {CA} .\frac{5}{4}\overrightarrow {CA}  = \frac{5}{4}A{C^2} = \frac{{5{a^2}}}{4}\)

           + \(\overrightarrow {CA} .\overrightarrow {CB}  = CA.CB.\cos \widehat {ACB} = a.a.\cos {60^0} = \frac{{{a^2}}}{2}\)

\( \Rightarrow \overrightarrow {AM} .\overrightarrow {BN}  = \overrightarrow {CM} .\overrightarrow {CN}  - \overrightarrow {CM} .\overrightarrow {CB}  - \overrightarrow {CA} .\overrightarrow {CN}  + \overrightarrow {CA} .\overrightarrow {CB}  = \frac{{5{a^2}}}{{12}} - \frac{{2{a^2}}}{3} - \frac{{5{a^2}}}{4} + \frac{{{a^2}}}{2} =  - {a^2}\)

Vậy \(\overrightarrow {AB} .\overrightarrow {AC}  = \frac{{{a^2}}}{2}\), \(\overrightarrow {AM} .\overrightarrow {BN}  =  - {a^2}\)

b) Ta có: \(M{N^2} = {\left( {\overrightarrow {MN} } \right)^2} = {\left( {\overrightarrow {MB}  + \overrightarrow {BC}  + \overrightarrow {CN} } \right)^2} = {\left( { - \frac{1}{3}\overrightarrow {BC}  + \overrightarrow {BC}  + \frac{5}{4}\overrightarrow {CA} } \right)^2}\) 

                      \( = {\left( {\frac{2}{3}\overrightarrow {BC}  + \frac{5}{4}\overrightarrow {CA} } \right)^2} = \frac{4}{9}B{C^2} + \frac{{25}}{{16}}A{C^2} + \frac{5}{3}\overrightarrow {BC} .\overrightarrow {CA} \)

                      \( = \frac{{289}}{{144}}{a^2} - \frac{5}{3}\overrightarrow {CB} .\overrightarrow {CA}  = \frac{{289}}{{144}}{a^2} - \frac{5}{3}.CB.CA.\cos \widehat {BCA}\) \( = \frac{{289}}{{144}}{a^2} - \frac{5}{6}{a^2} = \frac{{169{a^2}}}{{144}}\)

\( \Rightarrow M{N^2} = \frac{{169{a^2}}}{{144}} \Rightarrow MN = \frac{{13a}}{{12}}\)

Bài 62 trang 106 SBT Toán 10 - Cánh Diều

Cho hình thoi ABCD cạnh a và \(\widehat A\)= 120°. Tính \(\overrightarrow {AC} .\overrightarrow {BC} \).

Phương pháp:

Bước 1: Sử dụng tính chất hình thoi để chứng minh ∆ABC đều

Bước 2: Sử dụng định nghĩa tích vô hướng của 2 vectơ để tính giá trị \(\overrightarrow {AC} .\overrightarrow {BC} \)

Lời giải:

Bài 63 trang 106 SBT Toán 10 - Cánh Diều

Cho bốn điểm A, B, C, D. Chứng minh \(\overrightarrow {AB} .\overrightarrow {CD}  + \overrightarrow {AC} .\overrightarrow {DB}  + \overrightarrow {AD} .\overrightarrow {BC}  = 0\) (*)

Phương pháp:

Tách vectơ và đưa về các vectơ chung gốc (gốc A)

Lời giải:

Biến đổi vế trái (*) ta có:

\(\overrightarrow {AB} .\overrightarrow {CD}  + \overrightarrow {AC} .\overrightarrow {DB}  + \overrightarrow {AD} .\overrightarrow {BC}  = \)\(\overrightarrow {AB} .\left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right) + \overrightarrow {AC} .\left( {\overrightarrow {AB}  - \overrightarrow {AD} } \right) + \overrightarrow {AD} .\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)\)

\( = \overrightarrow {AB} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AC}  + \overrightarrow {AB} .\overrightarrow {AC}  - \overrightarrow {AC} .\overrightarrow {AD}  + \overrightarrow {AC} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AD}  = 0\) = VP (*) (ĐPCM)

Bài 64 trang 106 SBT Toán 10 - Cánh Diều

Cho hình vuông ABCD, M là trung điểm của BC. N là điểm nằm giữa hai điểm A và C. Đặt \(x = \frac{{AN}}{{AC}}\). Tìm x thỏa mãn \(AM \bot BN\)

Lời giải:

Do \(AM \bot BN\) nên \(\overrightarrow {AM} .\overrightarrow {BN}  = 0\)

Ta có: \(x = \frac{{AN}}{{AC}} \Rightarrow AN = xAC \Rightarrow \overrightarrow {AN}  = x\overrightarrow {AC} \)

\(\overrightarrow {AM}  = \overrightarrow {BM}  - \overrightarrow {BA}  = \frac{1}{2}\overrightarrow {BC}  - \overrightarrow {BA} \) ; \(\overrightarrow {BN}  = \overrightarrow {AN}  - \overrightarrow {AB}  = x\overrightarrow {AC}  - \overrightarrow {AB} \)

Khi đó \(\overrightarrow {AM} .\overrightarrow {BN}  = 0\)\( \Leftrightarrow \left( {\frac{1}{2}\overrightarrow {BC}  - \overrightarrow {BA} } \right).\left( {x\overrightarrow {AC}  - \overrightarrow {AB} } \right) = 0\)

                                \( \Leftrightarrow \frac{x}{2}\overrightarrow {BC} .\overrightarrow {AC}  - \frac{1}{2}\overrightarrow {BC} .\overrightarrow {AB}  - x\overrightarrow {BA} .\overrightarrow {AC}  + \overrightarrow {BA} .\overrightarrow {AB}  = 0\)

                                \( \Leftrightarrow \frac{x}{2}.BC.\sqrt 2 BC.\cos {45^0} + x.AB.\sqrt 2 AB.\cos {45^0} - A{B^2} = 0\)

                                \( \Leftrightarrow \frac{x}{2} + x - 1 = 0 \Leftrightarrow x = \frac{2}{3}\)

Vậy với \(\frac{{AN}}{{AC}} = \frac{2}{3}\) thì \(AM \bot BN\)

Bài 65 trang 106 SBT Toán 10 - Cánh Diều

Cho tam giác ABC và G là trọng tâm của tam giác. Với mỗi điểm M, chứng minh rằng:

\(M{A^2} + M{B^2} + M{C^2} = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\) (*)

Lời giải:

Do G là trọng tâm tam giác ABC nên \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Biến đổi vế trái (*) ta có:

\(M{A^2} + M{B^2} + M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2}\)\( = {\left( {\overrightarrow {MG}  + \overrightarrow {GA} } \right)^2} + {\left( {\overrightarrow {MG}  + \overrightarrow {GB} } \right)^2} + {\left( {\overrightarrow {MG}  + \overrightarrow {GC} } \right)^2}\)

                                      \( = 3{\overrightarrow {MG} ^2} + {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} + 2\overrightarrow {MG} \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right)\)

                                      \( = 3{\overrightarrow {MG} ^2} + {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} + 2\overrightarrow {MG} .\overrightarrow 0 \)

                                      \( = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\) = VP (*) (ĐPCM)

Bài 66 trang 106 SBT Toán 10 - Cánh Diều

Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 650 km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 35 km/h. Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần mười theo đơn vị km/h).

Lời giải:

Gọi \(\overrightarrow {{v_0}} \) là vận tốc của máy bay khi không có gió \( \Rightarrow \left| {\overrightarrow {{v_0}} } \right| = 650\) (km/h)

      \(\overrightarrow {{v_1}} \) là vận tốc của gió \( \Rightarrow \left| {\overrightarrow {{v_1}} } \right| = 35\) (km/h)

      \(\overrightarrow {{v_2}} \) là vận tốc của máy bay khi có gió

Theo giả thiết, \(\overrightarrow {{v_2}}  = \overrightarrow {{v_0}}  + \overrightarrow {{v_1}} \) \( \Rightarrow {\left| {\overrightarrow {{v_2}} } \right|^2} = {\overrightarrow {{v_2}} ^2} = {\left( {\overrightarrow {{v_0}}  + \overrightarrow {{v_1}} } \right)^2}\)\( = {\left| {\overrightarrow {{v_0}} } \right|^2} + {\left| {\overrightarrow {{v_1}} } \right|^2} + 2\overrightarrow {{v_0}} .\overrightarrow {{v_1}} \)

                                                                           \( = {\left| {\overrightarrow {{v_0}} } \right|^2} + {\left| {\overrightarrow {{v_1}} } \right|^2} + 2\left| {\overrightarrow {{v_0}} } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow {{v_0}} ,\overrightarrow {{v_1}} } \right)\)

Mà \(\left( {\overrightarrow {{v_0}} ,\overrightarrow {{v_1}} } \right) = {45^0}\) nên \({\left| {\overrightarrow {{v_0}} } \right|^2} + {\left| {\overrightarrow {{v_1}} } \right|^2} + 2\left| {\overrightarrow {{v_0}} } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow {{v_0}} ,\overrightarrow {{v_1}} } \right) = {650^2} + {35^2} + 2.650.35.\cos {45^0}\)\( \approx 455898,36\)

\( \Rightarrow \left| {\overrightarrow {{v_2}} } \right| \approx 675,2\) (km/h)

Vậy tốc độ mới của máy bay là 675,2 km/h

 Sachbaitap.com