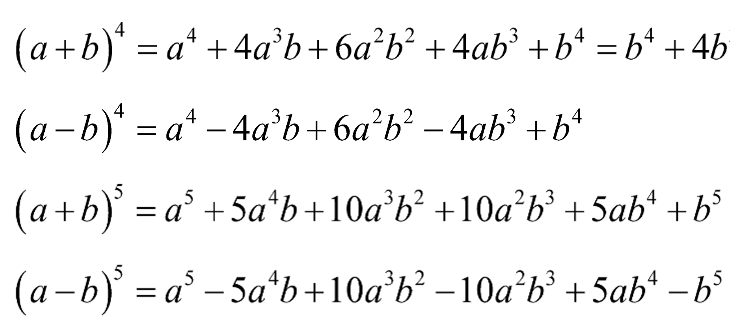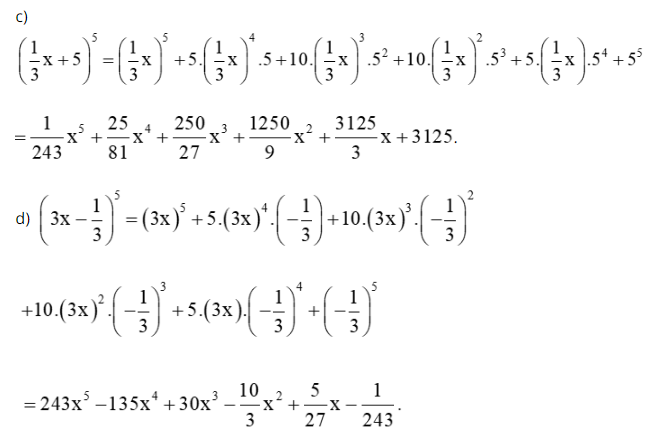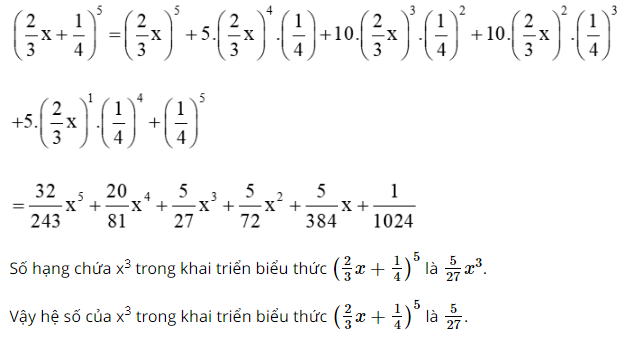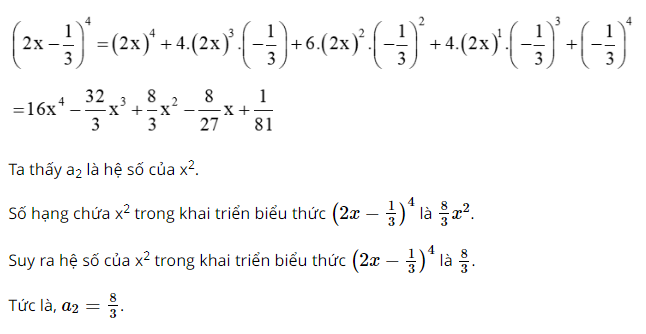Giải SBT Toán 10 trang 15, 16 Cánh Diều tập 2

Bài 28 trang 15 SBT Toán 10 - Cánh Diều

Trong các phát biểu sau, phát biểu nào sai? 

A.\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

B. \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\)

C. \({(a + b)^4} = {b^4} + 4{b^3}a + 6{a^2}{b^2} - 4b{a^3} + {a^4}\)

D. \({(a + b)^4} = {a^4} + {b^4}\)

Phương pháp:

Áp dụng nhị thức Newton để khai triển \({(a + b)^4}\)và \({(a - b)^4} = {\left[ {a + ( - b)} \right]^4}\) để tìm câu đúng

Lời giải:

Đáp án đúng là D

Công thức khai triển nhị thức Newton (a + b)⁴ là:

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ = b⁴ + 4b³a + 6b²a² + 4ba³ + a⁴.

Do đó phương án A, C đúng, phương án D sai.

Công thức khai triển nhị thức Newton (a – b)⁴ là:

(a + b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴.

Do đó phương án B đúng.

Vậy ta chọn phương án D.

Bài 29 trang 16 SBT Toán 10 - Cánh Diều

Trong các phát biểu sau, phát biểu nào đúng?

A.\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)

B. \({(a - b)^5} = {a^5} - 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} - 5a{b^4} + {b^5}\)

C. \({(a + b)^5} = {a^5} + {b^5}\)

D. \({(a - b)^5} = {a^5} - {b^5}\)

Phương pháp:

Áp dụng nhị thức Newton để khai triển \({(a + b)^5}\) để tìm câu đúng

Lời giải:

Công thức khai triển nhị thức Newton (a + b)⁵ là:

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Do đó phương án A đúng, phương án C sai.

Công thức khai triển nhị thức Newton (a – b)⁵ là:

(a – b)⁵ = a⁵ – 5a⁴b + 10a³b² – 10a²b³ + 5ab⁴ – b⁵.

Do đó các phương án B, D sai.

Vậy ta chọn phương án A.

Bài 30 trang 16 SBT Toán 10 - Cánh Diều

Hệ số của \({x^3}\) trong khai triển biểu thức \({(2x - 1)^4}\) là:

A. 32                           B. -32                          C. 8                             D. -8

Phương pháp:

Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\) với a = 2x và b = 1

Lời giải:

Đáp án đúng là B

Ta có: (2x – 1)⁴ = (2x)⁴ – 4.(2x)³.1 + 6.(2x)².1² – 4.(2x).1³ + 1⁴

= 16x⁴ – 32x³ + 24x² – 8x + 1

Số hạng chứa x³ trong khai triển biểu thức (2x – 1)⁴ là –32x³.

Vậy hệ số của x³ trong khai triển biểu thức (2x – 1)⁴ là –32.

Do đó ta chọn phương án B.

Bài 31 trang 16 SBT Toán 10 - Cánh Diều

Hệ số của x trong khai triển biểu thức \({(x - 2)^5}\) là:

A. 32               B. -32              C. 80               D. -80

Phương pháp:

Áp dụng công thức khai triển: \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\) với a = 1 và b = -2

Lời giải:

Đáp án đúng là C

Ta có: (x – 2)⁵ = x⁵ – 5x⁴.2 + 10x³.2² – 10x².2³ + 5x.2⁴ – 2⁵

= x⁵ – 10x⁴ + 40x³ – 80x² + 80x – 32

Số hạng chứa x trong khai triển biểu thức (x – 2)⁵ là 80x.

Vậy hệ số của x trong khai triển biểu thức (x – 2)⁵ là 80.

Do đó ta chọn phương án C.

Bài 32 trang 16 SBT Toán 10 - Cánh Diều

Khai triển các biểu thức sau:

a) \({(4x + 1)^4}\)                   b) \({(5x - 3)^4}\)                   c) \({\left( {\frac{1}{3}x + 5} \right)^5}\)                      d) \({\left( {3x - \frac{1}{3}} \right)^5}\)

Phương pháp:

Áp dụng các công thức khai triển:

Lời giải:

a) (4x + 1)⁴ = (4x)⁴ + 4.(4x)³.1 + 6.(4x)².1² + 4.4x.1³ + 1⁴

= 256x⁴ + 256x³ + 96x² + 16x + 1.

b) (5x – 3)⁴ = (5x)⁴ + 4.(5x)³.(–3) + 6.(5x)².(–3)² + 4.5x.(–3)³ + (–3)⁴

= 625x⁴ – 1500x³ + 1350x² – 540x + 81.

Bài 33 trang 16 SBT Toán 10 - Cánh Diều

Xác định hệ số của \({x^2}\) trong khai triển biểu thức \({(4x - 3)^4}\)

Phương pháp:

Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\)

Lời giải:

Ta có: (4x – 3)⁴ = (4x)⁴ – 4.(4x)³.3 + 6.(4x)².3² – 4.4x.3³ + 3⁴

= 256x⁴ – 768x³ + 864x² – 432x + 81

Số hạng chứa x² trong khai triển biểu thức (4x – 3)⁴ là 864x².

Vậy hệ số của x² trong khai triển biểu thức (4x – 3)⁴ là 864.

 Bài 34 trang 16 SBT Toán 10 - Cánh Diều

Xác định hệ số của \({x^3}\) trong khai triển biểu thức \({\left( {\frac{2}{3}x + \frac{1}{4}} \right)^5}\)

Phương pháp:

Áp dụng công thức khai triển \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)

Lời giải:

Ta có:

Bài 35 trang 16 SBT Toán 10 - Cánh Diều

Cho \({\left( {2x - \frac{1}{3}} \right)^4} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4}\). Tính: 

a) \({a_2}\)

b) \({a_0} + {a_1} + {a_2} + {a_3} + {a_4}\)

Phương pháp:

Bước 1: Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\) với \(a = 2x,b = \frac{1}{3}\)

Bước 2: Thay x = 1 vào khai triển trong giả thiết để tính tổng các hệ số của khai triển

Lời giải:

a) Ta có:

Bài 36 trang 16 SBT Toán 10 - Cánh Diều

Cho \({\left( {\frac{3}{5}x + \frac{1}{2}} \right)^5} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + {a_5}{x^5}\). Tính: 

a) \({a_3}\)

b) \({a_0} + {a_1} + {a_2} + {a_3} + {a_4} + {a_5}\)

Phương pháp:

Bước 1: Áp dụng công thức khai triển: \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\) với \(a = \frac{3}{5}x,b = \frac{1}{2}\)

Bước 2: Thay x = 1 vào khai triển trong giả thiết để tính tổng các hệ số của khai triển

Lời giải:

Ta có:

Bài 37 trang 16 SBT Toán 10 - Cánh Diều

Tính các tổng sau (Không sử dụng máy tính cầm tay):

a) \(T = C_4^0 + \frac{1}{2}C_4^1 + \frac{1}{3}C_4^2 + \frac{1}{4}C_4^3 + \frac{1}{5}C_4^4\)

b) \(S = C_6^1 + 2C_6^2 + 3C_6^3 + 4C_6^4 + 5C_5^6 + 6C_6^6\)

Phương pháp:

Bước 1: Ở ý a) áp dụng kết quả \(\frac{1}{{k + 1}}C_n^k = \frac{1}{{n + 1}}C_{n + 1}^{k + 1}\) với \(0 \le k \le n\) (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2) và khai triển (a + b)⁵ với a = 1 và b = 1

Bước 2: Ở ý b) áp dụng kết quả  \(kC_n^k = nC_{n - 1}^{k - 1}\) với \(1 \le k \le n\)  (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2) và khai triển (a + b)⁵ với a = 1 và b = 1

Lời giải:

Sachbaitap.com