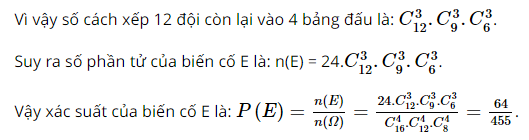Giải SBT Toán 10 trang 47, 48 Cánh Diều tập 2Giải bài 27, 28, 29, 30, 31 trang 47, bài 32, 33, 34, 35, 36 trang 48 SBT Toán 10 Cánh Diều tập 2. Xét phép thử “Gieo một con xúc xắc hai lần liên tiếp”. Biến cố nào dưới đây là biến cố không? Từ bộ rút lơ khơ có 52 quân bài thường đang được úp, rút ngẫu nhiên đồng thời 4 quân bài. Tính xác suất các biến cố sau: Bài 27 trang 47 SBT Toán 10 - Cánh Diều Xét phép thử “Gieo một con xúc xắc hai lần liên tiếp”. Biến cố nào dưới đây là biến cố không? A. Tổng số chấm ở hai lần gieo nhỏ hơn hoặc bằng 1 B. Cả hai lần gieo đều xuất hiện số chấm lẻ C. Số chấm xuất hiện ở hai lần gieo đều chia hết cho 5 D. Số chấm ở lần gieo thứ nhất nhỏ hơn số chấm ở lần gieo thứ hai Phương pháp: Biến cố không là biến cố không thể xảy ra \( \Rightarrow P\left( A \right) = 0\) Lời giải: Biến cố ở phương án A là biến cố không. Biến cố ở phương án B không phải biến cố không (vì có phần tử (1; 3) thuộc biến cố ở phương án B). Biến cố ở phương án C không phải biến cố không (vì có phần tử (5; 5) thuộc biến cố ở phương án C). Biến cố ở phương án D không phải biến cố không (vì có phần tử (2; 3) thuộc biến cố ở phương án D). Vậy ta chọn phương án A. Bài 28 trang 47 SBT Toán 10 - Cánh Diều Xét phép thử “Tung một đồng xu hai lần liên tiếp”. Biến cố nào dưới đây là biến cố chắc chắn? A. Mặt sấp chỉ xuất hiện 1 lần B. Lần thứ hai xuất hiện mặt ngửa C. Lần thứ nhất xuất hiện mặt sấp hoặc mặt ngửa D. Cả hai lần tung đều xuất hiện mặt sấp Phương pháp: Biến cố chắc chắn là biến cố chắc chắn xảy ra \( \Rightarrow P\left( A \right) = 1\) Lời giải: Không gian mẫu của phép thử trên là: Ω = {SS; SN; NS; NN}. Biến cố “Mặt sấp chỉ xuất hiện 1 lần” có tập hợp là: A = {SN; NS} ≠ Ω. Vì vậy biến cố ở phương án A không phải là biến cố chắc chắn. Biến cố “Lần thứ hai xuất hiện mặt ngửa” có tập hợp là: B = {SN; NN} ≠ Ω. Vì vậy biến cố ở phương án B không phải là biến cố chắc chắn. Biến cố “Lần thứ nhất xuất hiện mặt sấp hoặc mặt ngửa” có tập hợp là: C = {SS; SN; NS; NN} = Ω. Vì vậy biến cố ở phương án C là biến cố chắc chắn. Biến cố “Cả hai lần tung đều xuất hiện mặt sấp” có tập hợp là: D = {SS} ≠ Ω. Vì vậy biến cố ở phương án D không phải là biến cố chắc chắn. Vậy ta chọn phương án C. Bài 29 trang 47 SBT Toán 10 - Cánh Diều Cho tập hợp A gồm 2022 số nguyên dương liên tiếp: 1, 2, 3, …, 2022. Chọn ngẫu nhiên 2 số thuộc tập hợp A. Xác suất của biến cố “Tích 2 số được chọn là số chẵn” là: A. \(\frac{{C_{1011}^2}}{{C_{2022}^2}}\) B. \(1 - \frac{{C_{1011}^2}}{{C_{2022}^2}}\) C. \(\frac{1}{2}\) D. \(1 - \frac{{C_{2022}^2}}{{C_{4022}^2}}\) Lời giải: + Chọn ngẫu nhiên 2 số thuộc tập hợp A \( \Rightarrow n\left( \Omega \right) = C_{2022}^2\) + Tính xác suất để tích 2 số được chọn là số lẻ à 2 số được chọn đều là số lẻ à Chọn 2 trong số 1011 số lẻ của dãy \( \Rightarrow P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = 1 - \frac{{C_{1011}^2}}{{C_{2022}^2}}\) Chọn B. Bài 30 trang 47 SBT Toán 10 - Cánh Diều Ngân hàng đề thi của một môn Khoa học xã hội gồm 200 câu hỏi. Người ta chọn trong ngân hàng đề thi 5 câu hỏi để làm thành 1 đề thi, hai đề thi được gọi là giống nhau nếu có cùng tập hợp 5 câu hỏi. Một học sinh chắc chắn trả lời đúng 120 câu hỏi trong ngân hàng đề thi đó. Xác suất dể học sinh đó rút ngẫu nhiên được 1 đề thi mà có đúng 3 câu hỏi chắc chắn trả lời đúng là: A. \(\frac{{C_{120}^3}}{{C_{200}^5}}\) B. \(1 - \frac{{C_{80}^3}}{{C_{200}^5}}\) C. \(\frac{{120}}{{200}}\) D. \(\frac{{C_{80}^2C_{120}^3}}{{C_{200}^5}}\) Lời giải: + Chọn ngẫu nhiên 5 câu hỏi trong tập 200 câu\( \Rightarrow n\left( \Omega \right) = C_{200}^5\) + 3 câu chắc chắn trả lời đúng nằm trong 120 câu đã học và 2 câu còn lại nằm trong 80 câu còn lại \( \Rightarrow n\left( A \right) = C_{80}^2C_{120}^3\) \( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{80}^2C_{120}^3}}{{C_{200}^5}}\) Chọn D. Bài 31 trang 47 SBT Toán 10 - Cánh Diều Từ một hộp chứa 3 quả cầu trắng, 4 quả cầu đỏ, 5 quả cầu vàng, các quả cầu có kích thước và khối lượng giống nhau, lấy ngẫu nhiên đồng thời 3 quả cầu. Tính xác suất lấy được 3 quả cầu có màu đôi một khác nhau. Lời giải: + Mỗi cách lấy ra 3 quả cầu từ 12 quả cầu là tổ hợp chập 3 của 12 phần tử\( \Rightarrow n\left( \Omega \right) = C_{12}^3\) + Vì 3 quả cầu có màu đôi một khác nhau à Chọn 1 quả cầu trắng, 1 quả cầu đỏ, 1 quả cầu vàng \( \Rightarrow n\left( A \right) = 3.4.5 = 60\) \( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{60}}{{220}} = \frac{3}{{11}}\) Bài 32 trang 48 SBT Toán 10 - Cánh Diều Có 20 tấm thẻ màu xanh, 30 tấm thẻ màu đỏ. Người ta chọn ra đồng thời 18 tấm thẻ. Tính xác suất của biến cố A “Trong 18 tấm thẻ được chọn ra ít nhất một tấm thẻ màu xanh” Lời giải: + Mỗi cách chọn 18 tấm thẻ từ 50 tấm thẻ \( \Rightarrow n\left( \Omega \right) = C_{50}^{18}\) + Xét biến cố đối \(\overline A \): “Trong 18 tấm thẻ được chọn ra không có tấm thẻ màu xanh” là biến cố đối của biến cố A \( \Rightarrow n\left( {\overline A } \right) = C_{30}^{18}\) \( \Rightarrow P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = 1 - \frac{{C_{30}^{18}}}{{C_{50}^{18}}}\) Bài 33 trang 48 SBT Toán 10 - Cánh Diều Lớp 10A có 16 nam và 24 nữ. Chọn ngẫu nhiên 5 bạn để phân công trực nhật. Tính xác suất của biến cố A “Trong 5 bạn được chọn có 2 bạn nam và 3 bạn nữ” Lời giải: + Mỗi cách chọn 5 bạn từ 40 học sinh \( \Rightarrow n\left( \Omega \right) = C_{40}^5\) + Chọn 2 bạn nam và 3 bạn nữ \( \Rightarrow n\left( A \right) = C_{16}^2.C_{24}^3\) \( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^2.C_{24}^3}}{{C_{40}^5}} = \frac{{10120}}{{27417}}\) Bài 34 trang 48 SBT Toán 10 - Cánh Diều Xếp ngẫu nhiên 6 bạn An, Bình, Cường, Dũng, Đông, Huy vào một dãy hàng dọc. Tính xác suất của các biến cố sau: a) A: “Bạn Dũng luôn đứng liền sau bạn Bình” b) B: “Bạn Bình và bạn Cường luôn đứng liền nhau” Lời giải: Xếp 6 bạn thành 1 hàng dọc \( \Rightarrow n\left( \Omega \right) = 6! = 720\) a) A: “Bạn Dũng luôn đứng liền sau bạn Bình” \( \Rightarrow \) Coi bạn Dũng và Bình là 1 phần tử của hàng \( \Rightarrow \) Xếp 5 bạn còn lại thành 1 hàng ngang \( \Rightarrow n\left( A \right) = 5! = 120\) \( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{120}}{{720}} = \frac{1}{6}\) b) B: “Bạn Bình và bạn Cường luôn đứng liền nhau” \( \Rightarrow \) Coi bạn Bình và Cường là 1 phần tử của hàng \( \Rightarrow \) Xếp 5 bạn còn lại thành 1 hàng ngang \( \Rightarrow n\left( A \right) = 5!.2 = 240\) \( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{240}}{{720}} = \frac{1}{3}\) Bài 35 trang 48 SBT Toán 10 - Cánh Diều Từ bộ rút lơ khơ có 52 quân bài thường đang được úp, rút ngẫu nhiên đồng thời 4 quân bài. Tính xác suất các biến cố sau: a) A: “Rút được 4 quân bài cùng 1 giá trị” b) B: “Rút được 4 quân bài có cùng chất” c) C: “Trong 4 quân bài rút được chỉ có 2 quân Át” Lời giải: + Rút 4 quân bài (không sắp thứ tự) từ 52 quân bài \( \Rightarrow n\left( \Omega \right) = C_{52}^4\) a) A: “Rút được 4 quân bài cùng 1 giá trị” Trong bộ 52 quân bài có 13 nhóm 4 quân bài cùng một giá trị. \( \Rightarrow n\left( A \right) = 13\) \( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{13}}{{C_{52}^4}} = \frac{1}{{20825}}\) b) B: “Rút được 4 quân bài có cùng chất” Có 4 cách chọn chất của bộ bài. Mỗi chất có 13 quân bài. Số cách chọn 4 quân bài ở mỗi chất là số tổ hợp chập 4 của 13. \( \Rightarrow n\left( B \right) = 4.C_{13}^4\) \( \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{4.C_{13}^4}}{{C_{52}^4}} = \frac{{44}}{{4165}}\) c) C: “Trong 4 quân bài rút được chỉ có 2 quân Át” Số quân Át trong bộ bài là 4. Sau khi chọn 2 quân Át (từ 4 quân Át) thì 2 quân còn lại được chọn từ 48 quân bài bài không phải Át. \( \Rightarrow n\left( C \right) = C_4^2.C_{48}^2\) \( \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{C_4^2.C_{48}^2}}{{C_{52}^4}} = \frac{{6768}}{{270725}}\) Bài 36 trang 48 SBT Toán 10 - Cánh Diều Một giải đá bóng gồm 16 đội, trong đó có 4 đội của nước V. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 4 bảng đấu A, B, C, D, mỗi bảng đấu có 4 đội. Tính xác suất của biến cố “Bốn đội của nước V ở 4 bảng đấu khác nhau” Phương pháp: Xác suất của biến cố A là một số, kí hiệu \(P\left( A \right)\) được xác định bởi công thức: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\), trong đó \(n\left( A \right)\) và \(n\left( \Omega \right)\) lần lượt là kí hiệu số phần tử của tập A và \(\Omega \) Lời giải: Mỗi cách chọn 4 đội trong số 16 đội để xếp vào bảng A là một tổ hợp chập 4 của 16 phần tử. Mỗi cách chọn 4 đội tiếp theo trong số 12 đội còn lại để xếp vào bảng B là một tổ hợp chập 4 của 12 phần tử. Mỗi cách chọn 4 đội tiếp theo trong số 8 đội còn lại để xếp vào bảng C là một tổ hợp chập 4 của 8 phần tử. Lúc này, 4 đội cuối cùng sẽ được xếp vào bảng D.
 Gọi E là biến cố “Bốn đội của nước V ở 4 bảng đấu khác nhau”.
Số cách xếp 4 đội của nước V vào bảng đấu là 4! = 24. Mỗi cách chọn 3 đội trong 12 đội còn lại không phải của nước V để xếp vào bảng A là một tổ hợp chập 3 của 12 phần tử. Mỗi cách chọn 3 đội tiếp theo trong 9 đội còn lại không phải của nước V để xếp vào bảng B là một tổ hợp chập 3 của 9 phần tử. Mỗi cách chọn 3 đội tiếp theo trong 6 đội còn lại không phải của nước V để xếp vào bảng C là một tổ hợp chập 3 của 6 phần tử. Lúc này, 3 đội cuối cùng sẽ được xếp vào bảng D. Sachbaitap.com
Xem thêm tại đây:
Bài 5. Xác suất của biến cố
|
-

Giải SBT Toán 10 trang 48, 49, 50 Cánh Diều tập 2
Giải bài 37, 38, 39 trang 48, bài 40, 41, 42, 43 trang 49, bài 44, 45, 46, 47, 48 trang 50 SBT Toán 10 Cánh Diều tập 2. Số quy tròn của số gần đúng 38,4753701 với độ chính xác 0,005 là. Gieo một xúc sắc hai lần liên tiếp. Xác suất của biến cố “Tích số chấm trong hai lần gieo là số chẵn” là:

 Tải ngay
Tải ngay