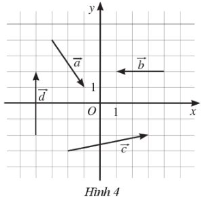
Giải SBT Toán 10 trang 61, 62 Cánh Diều tập 2

Bài 1 trang 61 SBT Toán 10 - Cánh Diều

Toạ độ của vectơ \(\overrightarrow u  =  - 3\overrightarrow i  + 2\overrightarrow j \) là:

A. \(( - 3;2)\)               B. \((2; - 3)\)              

C. \(( - 3\overrightarrow i ;2\overrightarrow j )\)                    D. \((3;2)\)

Phương pháp:

Áp dụng định lí: Nếu \(\overrightarrow u  = a\overrightarrow i  + b\overrightarrow j \) thì  \(\overrightarrow u  = (a;b)\)

Lời giải:

Vậy chọn đáp án A.

Bài 2 trang 61 SBT Toán 10 - Cánh Diều

Tọa độ của vectơ \(\overrightarrow u  = 5\overrightarrow j \) là:

A. \((5;0)\)                  B. \((5;\overrightarrow j )\)              C. \((0;5\overrightarrow j )\)                D. \((0;5)\)

Phương pháp:

Áp dụng định lí: Nếu \(\overrightarrow u  = a\overrightarrow i  + b\overrightarrow j \) thì  \(\overrightarrow u  = (a;b)\)

Lời giải:

Vậy chọn đáp án D.

Bài 3 trang 61 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho A(2; −5). Toạ độ của vectơ \(\overrightarrow {OA} \) là:

A. (2 ; 5)                     B. (2; −5)                    C. (−2; −5)                  D. (−2; 5)

Phương pháp:

Áp dụng định nghĩa tọa độ điểm M được gọi là tọa độ của vectơ \(\overrightarrow {OM} \)

Lời giải:

Bài 4 trang 61 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho A(−1; 3), B(2; −1). Toạ độ của vectơ \(\overrightarrow {AB} \) là:

A. (1; -4)                     B. (-3; 4)                     C. (3; -4)                     D. (1; -2)

Phương pháp:

Nếu \(A({x_A};{y_A}),B({x_B};{y_B})\) thì \(\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A})\)

Lời giải:

Vậy chọn đáp án C.

Bài 5 trang 61 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow u  = ( - 2; - 4),\overrightarrow v  = (2x - y;y)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu:

A.\(\left\{ \begin{array}{l}x = 1\\y =  - 4\end{array} \right.\)                   B. \(\left\{ \begin{array}{l}x =  - 3\\y =  - 4\end{array} \right.\)                       C. \(\left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right.\)                        D. \(\left\{ \begin{array}{l}x =  - 3\\y = 4\end{array} \right.\)

Lời giải:

Ta có: \(\overrightarrow u  = \overrightarrow v  \Leftrightarrow \left\{ \begin{array}{l}2x - y =  - 2\\y =  - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y =  - 4\end{array} \right.\) 

Chọn B

Bài 6 trang 61 SBT Toán 10 - Cánh Diều

Cho hình bình hành ABCD có A(–1 ; –2), B(3; 2), C(4; − 1). Toạ độ của đỉnh D là:

A. (8; 3)                      B. (3; 8)                       C. (-5; 0)                     D. (0; -5)

Lời giải:

Giả sử D(a; b) ta có \(\overrightarrow {DC}  = (4 - a; - 1 - b)\) và \(\overrightarrow {AB}  = (4;4)\)

ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC}  = \overrightarrow {AB}  \Leftrightarrow \left\{ \begin{array}{l}4 - a = 4\\ - 1 - b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b =  - 5\end{array} \right. \Rightarrow D(0; - 5)\) 

Chọn D

Bài 7 trang 61 SBT Toán 10 - Cánh Diều

Tìm toạ độ của các vectơ trong Hình 4.

Phương pháp:

Bước 1: Xác định tọa độ các điểm A, B, C, D sao cho \(\overrightarrow {OA}  = \overrightarrow a ;\overrightarrow {OB}  = \overrightarrow b ;\overrightarrow {OC}  = \overrightarrow c ;\overrightarrow {OD}  = \overrightarrow d \)

Bước 2: Tìm tọa độ các vectơ \(\overrightarrow a ;\overrightarrow b ;\overrightarrow c ;\overrightarrow d \) dựa vào tọa độ các vectơ \(\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD} \)

Lời giải:

- Vẽ \(\overrightarrow {OA}  = \overrightarrow a \), ta có \(A(2; - 3)\) nên \(\overrightarrow a  = (2; - 3)\)

- Vẽ \(\overrightarrow {OB}  = \overrightarrow b \), ta có \(B( - 3;0)\) nên \(\overrightarrow b  = ( - 3;0)\)

- Vẽ \(\overrightarrow {OC}  = \overrightarrow c \), ta có \(C(5;1)\) nên \(\overrightarrow c  = (5;1)\)

- Vẽ \(\overrightarrow {OD}  = \overrightarrow d \), ta có \(D(0;4)\) nên \(\overrightarrow d  = (0;4)\)

Bài 8 trang 62 SBT Toán 10 - Cánh Diều

Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:

a) \(\overrightarrow m  = (2a + 3;b - 1)\) và \(\overrightarrow n  = (1; - 2)\)

b) \(\overrightarrow u  = (3a - 2;5)\)và \(\overrightarrow v  = (5;2b + 1)\)

c) \(\overrightarrow x  = (2a + b;2b)\) và \(\overrightarrow y  = (3 + 2b;b - 3a)\)

Phương phảp:

\(\overrightarrow a  = ({x_1};{y_1})\) và \(\overrightarrow b  = ({x_2};{y_2})\) bằng nhau khi và chỉ khi \(\left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\)

Lời giải:

a) \(\overrightarrow m  = (2a + 3;b - 1)\) và \(\overrightarrow n  = (1; - 2)\)

\(\overrightarrow m  = \overrightarrow n  \Leftrightarrow \left\{ \begin{array}{l}2a + 3 = 1\\b - 1 =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b =  - 1\end{array} \right.\)

b) \(\overrightarrow u  = (3a - 2;5)\)và \(\overrightarrow v  = (5;2b + 1)\)

\(\overrightarrow u  = \overrightarrow v  \Leftrightarrow \left\{ \begin{array}{l}3a - 2 = 5\\5 = 2b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{3}\\b = 2\end{array} \right.\)

c) \(\overrightarrow x  = (2a + b;2b)\) và \(\overrightarrow y  = (3 + 2b;b - 3a)\)

\(\overrightarrow x  = \overrightarrow y  \Leftrightarrow \left\{ \begin{array}{l}2a + b = 3 + 2b\\2b = b - 3a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a - b = 3\\3a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{3}{5}\\b =  - \frac{9}{5}\end{array} \right.\)

Bài 9 trang 62 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 4 ; 2), B(2 ; 4), C(8 ; – 2). Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Phương pháp:

Bước 1: Tham số hóa tọa độ điểm D và xác định tọa độ vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)

Bước 2: Áp dụng kết quả tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC}  = \overrightarrow {AB} \) để tìm tọa độ điểm D

Lời giải:

Giả sử D(a; b) ta có \(\overrightarrow {DC}  = (8 - a; - 2 - b)\) và \(\overrightarrow {AB}  = (6;2)\)

ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC}  = \overrightarrow {AB}  \Leftrightarrow \left\{ \begin{array}{l}8 - a = 6\\ - 2 - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 4\end{array} \right. \Rightarrow D(2; - 4)\) 

Bài 10 trang 62 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho tứ giác ABCD có \(A({x_A};{y_A});B({x_B};{y_B});C({x_C};{y_C});D({x_D};{y_D})\). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi \({x_A} + {x_C} = {x_B} + {x_D}\) và \({y_A} + {y_C} = {y_B} + {y_D}\)

Lời giải:

Ta có: \(\overrightarrow {AB}  = ({x_B} - {x_A};{y_B} - {y_A})\) và \(\overrightarrow {DC}  = ({x_C} - {x_D};{y_C} - {y_D})\)

ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {CD}  \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_A} = {x_C} - {x_D}\\{y_B} - {y_A} = {y_C} - {y_D}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_D} = {x_C} + {x_A}\\{y_B} + {y_D} = {y_C} + {y_A}\end{array} \right.\)  (ĐPCM)

Bài 11 trang 62 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng M(1 ; – 2), N(3 ; 1), P(− 1 ; 2). Tìm toạ độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.

Lời giải:

Ta có: MN // PQ nên \(\overrightarrow {MN} \) và \(\overrightarrow {PQ} \) cùng phương

Mặt khác, PQ = 2MN \( \Rightarrow \overrightarrow {PQ}  = 2\overrightarrow {NM} \)

Gọi tọa độ điểm Q là \(Q(a;b)\). Ta có: \(\overrightarrow {PQ}  = (a + 1;b - 2)\) và \(\overrightarrow {NM}  = ( - 2; - 3)\)

\( \Rightarrow \overrightarrow {PQ}  = 2\overrightarrow {NM}  \Leftrightarrow \left\{ \begin{array}{l}a + 1 = 2.( - 2)\\b - 2 = 2.( - 3)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + 1 =  - 4\\b - 2 =  - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 5\\b =  - 4\end{array} \right.\) . Vậy Q(-5 ; -4)

Sachbaitap.com