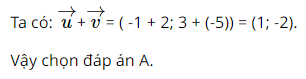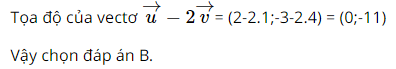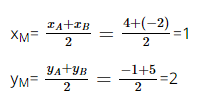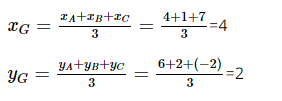Giải SBT Toán 10 trang 66, 67 Cánh Diều tập 2Giải bài 12, 13, 14, 15 16, 17 trang 66, bài 18, 19, 20, 21, 22, 23 trang 67 SBT Toán 10 Cánh Diều tập 2. Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(– 2 ; 4), B(– 5 ; − 1), C(8 ; – 2). Giải tam giác ABC (làm tròn các kết quả số đo góc đến hàng đơn vị). Bài 12 trang 66 SBT Toán 10 - Cánh Diều Cho hai vectơ \(\overrightarrow u = ( - 1;3)\) và \(\overrightarrow v = (2; - 5)\). Toạ độ của vectơ \(\overrightarrow u + \overrightarrow v \) là: A. (1; -2) B. (-2; 1) C. (-3; 8) D. (3; -8) Phương pháp: Nếu \(\overrightarrow u = ({x_1};{y_1})\) và \(\overrightarrow v = ({x_2};{y_2})\) thì \(\overrightarrow u + \overrightarrow v = ({x_1} + {x_2};{y_1} + {y_2})\) Lời giải: Bài 13 trang 66 SBT Toán 10 - Cánh Diều Cho hai vectơ \(\overrightarrow u = (2; - 3)\)và \(\overrightarrow v = (1;4)\). Toạ độ của vectơ \(\overrightarrow u - 2\overrightarrow v \) là: A. (0; 11) B. (0; -11) C. (-11; 0) D. (-3; 10) Phương pháp: Nếu \(\overrightarrow u = ({x_1};{y_1})\) và \(\overrightarrow v = ({x_2};{y_2})\) thì \(\overrightarrow u - 2\overrightarrow v = ({x_1} - 2{x_2};{y_1} - 2{y_2})\) Lời giải: Bài 14 trang 66 SBT Toán 10 - Cánh Diều Cho hai điểm A(4; − 1) và B(– 2; 5). Toạ độ trung điểm M của đoạn thẳng AB là: A. (2;4) B. (-3; 3) C. (3; -3) D. (1; 2) Phương phảp: Nếu M(a; b) là trung điểm của AB với \(A({x_A};{y_A}),B({x_B};{y_B})\) thì \(\left\{ \begin{array}{l}a = \frac{{{x_A} + {x_B}}}{2}\\b = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) Lời giải: Tọa độ trung điểm M của đoạn thẳng AB là: Suy ra M(1; 2) Vậy chọn đáp án D. Bài 15 trang 66 SBT Toán 10 - Cánh Diều Cho tam giác ABC có A(4 ; 6), B(1 ; 2), C(7 ; – 2). Toạ độ trọng tâm G của tam giác ABC là: \(A\left( {4;\frac{{10}}{3}} \right)\) B. (8; 4) C. (2;4) D. (4; 2). Phương pháp: Nếu G(a; b) là trọng tâm của ∆ABC với \(A({x_A};{y_A}),B({x_B};{y_B}),C({x_C};{y_C})\) thì \(\left\{ \begin{array}{l}a = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\b = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) Lời giải: Tọa độ trọng tâm G của tam giác ABC là: Suy ra G(4; 2) Vậy chọn đáp án D. Bài 16 trang 66 SBT Toán 10 - Cánh Diều Cho hai điểm M(− 2 ; 4) và N(1 ; 2). Khoảng cách giữa hai điểm M và N là: A. \(\sqrt {13} \) B. \(\sqrt 5 \) C. 13 D. \(\sqrt {37} \) Lời giải: Cho M(− 2 ; 4) và N(1 ; 2) \( \Rightarrow MN = \sqrt {{3^2} + {{( - 2)}^2}} = \sqrt {13} \) Chọn A Bài 17 trang 66 SBT Toán 10 - Cánh Diều Cho hai vectơ \(\overrightarrow u = ( - 4; - 3)\) và \(\overrightarrow v = ( - 1; - 7)\). Góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là: A. 90⁰ B. 60⁰ C. 45⁰ D. 30⁰ Lời giải: Ta có: \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{( - 4).( - 1) + ( - 3).( - 7)}}{{\sqrt {{{( - 4)}^2} + {{( - 3)}^2}} .\sqrt {{{( - 1)}^2} + {{( - 7)}^2}} }}\)\( = \frac{{\sqrt 2 }}{2}\) \( \Rightarrow \left( {\overrightarrow u ,\overrightarrow v } \right) = {45^0}\) Chọn C Bài 18 trang 67 SBT Toán 10 - Cánh Diều Côsin của góc giữa hai vectơ \(\overrightarrow u = (1;1)\) và \(\overrightarrow v = ( - 2;1)\) là: A. \( - \frac{1}{{10}}\) B. \(\frac{{\sqrt {10} }}{{10}}\) C. \( - \frac{{\sqrt {10} }}{{10}}\) D. \(\frac{3}{{10}}\) Lời giải: Ta có: \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{1.( - 2) + 1.1}}{{\sqrt {{1^2} + {1^2}} .\sqrt {{{( - 2)}^2} + {1^2}} }}\)\( = - \frac{{\sqrt {10} }}{{10}}\) Chọn C Bài 19 trang 67 SBT Toán 10 - Cánh Diều Cho tam giác ABC có A(2 ; 6), B(– 2 ; 2), C(8 ; 0). Khi đó, tam giác ABC là: A. Tam giác đều B. Tam giác vuông tại A C. Tam giác có góc tù tại A D. Tam giác cân tại A Lời giải: \(\overrightarrow {AB} = ( - 4; - 4) \Rightarrow AB = 4\sqrt 2 \); \(\overrightarrow {AC} = (6; - 6) \Rightarrow AC = 6\sqrt 2 \); \(\overrightarrow {BC} = (10; - 2) \Rightarrow BC = 2\sqrt {26} \) Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = ( - 4).6 + ( - 4).( - 6) = - 24 + 24 = 0\) \( \Rightarrow AB \bot AC\) Vậy ∆ABC vuông tại A Chọn B Bài 20 trang 67 SBT Toán 10 - Cánh Diều Trong mặt phẳng toạ độ Oxy, cho ba điểm A(1; 5), B(–1; –1), C(2; – 5). a) Chứng minh ba điểm A, B, C không thẳng hàng b) Tìm toạ độ trọng tâm G của tam giác ABC c) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD = \(\frac{3}{2}\)AB Lời giải: a) Ta có: \(\overrightarrow {AB} = ( - 2; - 6)\); \(\overrightarrow {AC} = (1; - 10)\). Vì \(\frac{{ - 2}}{1} \ne \frac{{ - 6}}{{ - 10}}\) nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương. Vậy ba điểm A, B, C không thẳng hàng b) G(a; b) là trọng tâm của ∆ABC \( \Rightarrow G\left( {\frac{2}{3}; - \frac{1}{3}} \right)\) c) Gọi \(D(a;b)\) Theo giả thiết, ABCD là hình thang có AB // CD và CD = \(\frac{3}{2}\)AB \( \Rightarrow \overrightarrow {CD} = \frac{3}{2}\overrightarrow {BA} \) Ta có: \(\overrightarrow {CD} = (a - 2;b + 5),\overrightarrow {AB} = ( - 2; - 6)\) \( \Rightarrow \overrightarrow {CD} = \frac{3}{2}\overrightarrow {BA} \)\( \Leftrightarrow \left\{ \begin{array}{l}a - 2 = \frac{3}{2}.2\\b + 5 = \frac{3}{2}.6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5\\b = 4\end{array} \right.\). Vậy D(5; 4) Bài 21 trang 67 SBT Toán 10 - Cánh Diều Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(– 2 ; 4), B(– 5 ; − 1), C(8 ; – 2). Giải tam giác ABC (làm tròn các kết quả số đo góc đến hàng đơn vị). Phương pháp: Bước 1: Tính độ dài các cạnh AB, AC, BC Bước 2: Sử dụng định lí cosin, định lí sin để tính số đo góc Lời giải: \(\overrightarrow {AB} = ( - 3; - 5) \Rightarrow AB = \sqrt {34} \); \(\overrightarrow {AC} = (10; - 6) \Rightarrow AC = 2\sqrt {34} \); \(\overrightarrow {BC} = (13; - 1) \Rightarrow BC = \sqrt {170} \) Áp dụng định lí cosin cho tam giác ABC ta có: \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = 0\)\( \Rightarrow \widehat A = {90^0}\) \(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{\sqrt 5 }}{5}\)\( \Rightarrow \widehat B \approx {63^0}\) \( \Rightarrow \widehat C = {90^0} - \widehat B \approx {27^0}\) Bài 22 trang 67 SBT Toán 10 - Cánh Diều Trong mặt phẳng toạ độ Oxy, cho hai điểm A(4 ; −2), B(10; 4) và điểm M nằm trên trục Ox. Tìm toạ độ điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) có giá trị nhỏ nhất. Lời giải: Do M \( \in Ox\) nên M(a; 0) Gọi I là trung điểm AB \( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \) và I(7; 1) Ta có: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {MI} + \overrightarrow {IB} } \right| = \left| {2\overrightarrow {MI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right)} \right| = 2\left| {\overrightarrow {MI} } \right|\)\( = 2MI\) \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) có giá trị nhỏ nhất khi và chỉ khi MI nhỏ nhất \( \Leftrightarrow \) M là hình chiếu của I trên Ox Mà I(7; 1) \( \Rightarrow M(7;0)\) Vậy M(7; 0) thì \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) có giá trị nhỏ nhất Bài 23 trang 67 SBT Toán 10 - Cánh Diều Trên màn hình ra đa của đài kiểm soát không lưu (được coi như mặt phẳng toạ độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), một máy bay trực thăng chuyển động thẳng đều từ thành phố A có toạ độ (600 ; 200) đến thành phố B có toạ độ (200 ; 500) và thời gian bay quãng đường AB là 3 giờ. Hãy tìm toạ độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ. Lời giải: Gọi C (a; b) là địa điểm máy bay đến sau khi xuất phát 1 giờ Ta có: \(\overrightarrow {AB} = ( - 400;300)\) Theo giả thiết, AC = \(\frac{1}{3}AB\) \( \Rightarrow \overrightarrow {AC} = \frac{1}{3}\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}a - 600 = \frac{1}{3}.( - 400)\\b - 200 = \frac{1}{3}.300\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{1400}}{3}\\b = 300\end{array} \right. \Rightarrow C\left( {\frac{{1400}}{3};300} \right)\) Vậy toạ độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ là \(\left( {\frac{{1400}}{3};300} \right)\). Sachbaitap.com
Xem thêm tại đây:
Bài 2. Biểu thức tọa độ của các phép toán vectơ
|
-

Giải SBT Toán 10 trang 73, 74 Cánh Diều tập 2
Giải bài 24, 25, 26, 27, 28, 29, 30 trang 73, bài 31, 32 trang 74 SBT Toán 10 Cánh Diều tập 2. Cho đường thẳng ∆: x − 3y + 4 = 0. Phương trình nào dưới đây là phương trình tham số của ∆?

 Tải ngay
Tải ngay