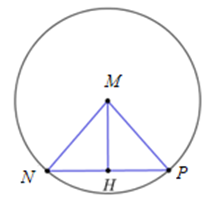
Giải SBT Toán 10 trang 88, 89, 90 Cánh Diều tập 2

Bài 47 trang 88 SBT Toán 10 - Cánh Diều

Phương trình nào sau đây không là phương trình đường tròn?

A. x² + y² = 4                                       B. x² + y² + 2x – 1 = 0            

C. 2x² + 3y² + 2x + 3y = 9                   D. x² + y² + 4y + 3 = 0

Phương pháp:

Bước 1: Tìm các PT có hệ số của x² và y² khác nhau để tìm ra PT không là PT đường tròn

Bước 2: Nếu các PT đều có hệ số x² và y² bằng nhau thì biến đổi các PT còn lại về dạng \({(x - a)^2} + {(y - b)^2} = c\)

Bước 3: Xét dấu của c, nếu c ≤ 0 thì PT đó không là phương trình đường tròn

Lời giải:

Ta thấy PT 2x² + 3y² + 2x + 3y = 9 có hệ số của x² và y² khác nhau nên không là phương trình đường tròn

 Chọn C

Bài 48 trang 88 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x + 8)² + (y – 10)² = 36. Toạ độ tâm I của (C) là:

A. (8; -10)                   B. (-8; 10)                   C. (-10; 8)                   D. (10; -8)

Phương pháp:

Đường tròn có PT \({(x - a)^2} + {(y - b)^2} = {R^2}\) có tâm I(a ; b)

Lời giải:

Dễ dàng ta thấy theo dạng phương trình đường tròn (x-a)²+(y-b)²=R² thì tâm I của (C) có tọa độ là I(-8; 10).

Vậy chọn đáp án B.

Bài 49 trang 88 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x − 1)² + (y + 2)² = 4. Bán kính của (C) bằng:

A. 4                             B. 16                           C. 2                             D. 1

Phương pháp:

Đường tròn có PT \({(x - a)^2} + {(y - b)^2} = c\) với c > 0 có bán kính \(R = \sqrt c \)

Lời giải:

Vậy chọn đáp án C.

Bài 50 trang 89 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, đường tròn tâm I(− 4 ; 2) bán kính R = 9 có phương trình là:

A. (x - 4)² + (y + 2)² = 81                               B. (x + 4)² + (y - 2)² = 9

C. (x - 4)² + (y + 2)² = 9                                  D. (x + 4)² + (y - 2)² = 81

Phương pháp:

Đường tròn (C) có tâm I(a ; b), bán kính R có PT dạng chính tắc: (C): \({(x - a)^2} + {(y - b)^2} = {R^2}\)

Lời giải:

Đường tròn tâm I(- 4; 2) bán kính R = 9 có phương trình là: (x+4)²+(y-2)²=81

Vậy chọn đáp án D.

Bài 51 trang 89 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x − 3)² + (y − 4)² = 25. Tiếp tuyến tại điểm M(0; 8)  thuộc đường tròn có một vectơ pháp tuyến là:

A. \(\overrightarrow n  = ( - 3;4)\)               B. \(\overrightarrow n  = (3;4)\)                     

C. \(\overrightarrow n  = (4; - 3)\)               D. \(\overrightarrow n  = (4;3)\)

Phương pháp:

Giả sử d là tiếp tuyến tại M của (C). Khi đó \(IM \bot d\) (I là tâm của (C)) nên d nhận vectơ \(\overrightarrow {OM} \) làm VTPT

Lời giải:

(C) có tâm I(3; 4), bán kính R = 5

Giả sử d là tiếp tuyến tại M của (C) \( \Rightarrow IM \bot d\) \( \Rightarrow \) d nhận \(\overrightarrow {IM} \) làm VTPT

\( \Rightarrow \)\(\overrightarrow {IM}  = ( - 3;4)\)   

Chọn A

Bài 52 trang 89 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x – 6)² + (y – 7)² = 16. Hai điểm M, N chuyển động trên đường tròn (C). Khoảng cách lớn nhất giữa hai điểm M và N bằng:

A. 16                           B. 8                             C. 4                             D. 256

Phương pháp:

Khoảng cách lớn nhất giữa hai điểm trên đường tròn là đường kính của đường tròn

Lời giải:

Do M, N chuyển động trên đường tròn nên khoảng cách lớn nhất giữa 2 điểm M, N chính bằng đường kính của đường tròn.

Vậy độ dài lớn nhất của MN = 2R = 8. Chọn đáp án B.

Bài 53 trang 89 SBT Toán 10 - Cánh Diều

Tìm k sao cho phương trình: x² + y² – 6x + 2ky + 2k + 12 = 0 là phương trình đường tròn.

Lời giải:

PT x² + y² – 6x + 2ky + 2k + 12 = 0 (1) có các giá trị a = 3, b = -k, c = 2k + 12

(1) là PT đường tròn khi và chỉ khi 3² + k² – 2k – 12 > 0 \( \Leftrightarrow {k^2} - 2k - 3 > 0 \Leftrightarrow \left[ \begin{array}{l}k > 3\\k <  - 1\end{array} \right.\)

Vậy với \(k > 3\) hoặc \(k <  - 1\) thì PT (1) là phương trình đường tròn

Bài 54 trang 89 SBT Toán 10 - Cánh Diều

Viết phương trình đường tròn (C) trong mỗi trường hợp sau:

a) (C) có tâm I(−6 ; 2) bán kính 7

b) (C) có tâm I(3 ; – 7) và đi qua điểm A(4 ; 1)

c) (C) có tâm I(1 ; 2) và tiếp xúc với đường thẳng 3x + 4y + 19 = 0

d) (C) có đường kính AB với A(−2 ; 3) và B(0 ; 1)

e) (C) có tâm I thuộc đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 1 - t\end{array} \right.\) và (C) tiếp xúc với hai đường thẳng ∆₂: 3x + 4y – 1 = 0, ∆₃: 3x - 4y + 2 = 0

Lời giải:

a) (C) có tâm I(−6 ; 2) bán kính 7 nên có PT: \({(x + 6)^2} + {(y - 2)^2} = 49\)

b) (C) có tâm I(3 ; – 7) và đi qua điểm A(4 ; 1) \( \Rightarrow \) Bán kính của (C) là \(IA = \sqrt {{{(4 - 3)}^2} + {{(1 + 7)}^2}}  = \sqrt {65} \)

\( \Rightarrow \)(C) có PT: \({(x - 3)^2} + {(y + 7)^2} = 65\)

c) (C) có tâm I(1 ; 2) và tiếp xúc với đường thẳng 3x + 4y + 19 = 0

\( \Rightarrow \) Bán kính của (C) là khoảng cách từ tâm I đến đường thẳng ∆: 3x + 4y + 19 = 0

Ta có: \(d(I,\Delta ) = \frac{{\left| {3.1 + 4.2 + 19} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{30}}{5} = 6\)

\( \Rightarrow \)(C) có PT: \({(x - 1)^2} + {(y - 2)^2} = 36\)

d) (C) có đường kính AB với A(−2 ; 3) và B(0 ; 1)

\( \Rightarrow \) (C) có tâm I là trung điểm của AB \( \Rightarrow I( - 1;2)\)

(C) có bán kính IA = IB = \(\sqrt 2 \)

\( \Rightarrow \)(C) có PT: \({(x + 1)^2} + {(y - 2)^2} = 2\)

e) (C) có tâm I thuộc đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 1 - t\end{array} \right.\) và (C) tiếp xúc với hai đường thẳng ∆₂: 3x + 4y – 1 = 0, ∆₃: 3x - 4y + 2 = 0

Do \(I \in {\Delta _1}\) nên \(I(1 + t;1 - t)\)

Theo giả thiết, \(R = d(I,{\Delta _2}) = d(I,{\Delta _3}) \Leftrightarrow \frac{{\left| {3(1 + t) + 4(1 - t) - 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{\left| {3(1 + t) - 4(1 - t) + 2} \right|}}{{\sqrt {{3^2} + {{( - 4)}^2}} }}\)

                                                        \( \Leftrightarrow \left| {6 - t} \right| = \left| {7t + 1} \right| \Leftrightarrow \left[ \begin{array}{l}6 - t = 7t + 1\\6 - t =  - 7t - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = \frac{5}{8}\\t = \frac{{ - 7}}{6}\end{array} \right.\)

Với \(t = \frac{5}{8} \Rightarrow I\left( {\frac{{13}}{8};\frac{3}{8}} \right)\) \( \Rightarrow \)\(R = \frac{{43}}{{40}}\). Khi đó (C) có PT: \({\left( {x - \frac{{13}}{8}} \right)^2} + {\left( {y - \frac{3}{8}} \right)^2} = \frac{{1849}}{{1600}}\)

Với \(t =  - \frac{7}{6} \Rightarrow I\left( { - \frac{1}{6};\frac{{13}}{6}} \right)\)\( \Rightarrow \)\(R = \frac{{43}}{{30}}\). Khi đó (C) có PT: \({\left( {x + \frac{1}{6}} \right)^2} + {\left( {y - \frac{{13}}{6}} \right)^2} = \frac{{1849}}{{900}}\)

Bài 55 trang 89 SBT Toán 10 - Cánh Diều

Lập phương trình đường thẳng ∆ là tiếp tuyến của đường tròn (C): (x + 2)² + (y − 3)² = 4 trong mỗi trường hợp sau:

a) ∆ tiếp xúc (C) tại điểm có tung độ bằng 3

b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0

c) ∆ đi qua điểm D(0 ; 4)

Lời giải:

(C) có tâm I(-2 ; 3), bán kính R = 2

a) Theo giả thiết, điểm M(m; 3) là tiếp điểm của ∆ và (C)

Ta có: \(IM = 2 \Leftrightarrow I{M^2} = 4 \Leftrightarrow {(m + 2)^2} = 4 \Leftrightarrow \left[ \begin{array}{l}m + 2 = 2\\m + 2 =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m =  - 4\end{array} \right.\)

Với m = 0 thì M(0 ; 3) \( \Rightarrow \)∆ đi qua M và nhận \(\overrightarrow {IM}  = (2;0)\) làm VTPT nên có PT: x = 0

Với m = -4 thì M(-4 ; 3) \( \Rightarrow \)∆ đi qua M và nhận \(\overrightarrow {IM}  = ( - 2;0)\) làm VTPT nên có PT: x + 4 = 0

b) Theo giả thiết, ∆ vuông góc với đường thẳng d: 5x – 12y + 1 = 0 mà d có VTPT \(\overrightarrow {{n_d}}  = (5; - 12)\)

\( \Rightarrow \Delta \) nhận \(\overrightarrow n  = (12;5)\) làm VTPT \( \Rightarrow \Delta \) có PTTQ: 12x + 5y + c = 0

Ta có: \(d(I,\Delta ) = R \Leftrightarrow \frac{{\left| {12.( - 2) + 5.3 + c} \right|}}{{\sqrt {{{12}^2} + {5^2}} }} = 2\)\( \Leftrightarrow \left| {c - 9} \right| = 26 \Leftrightarrow \left[ \begin{array}{l}c - 9 = 26\\c - 9 =  - 26\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 35\\c =  - 17\end{array} \right.\)

Với c = 35 thì ∆ có PT: 12x + 5y + 35 = 0

Với c = -17 thì ∆ có PT: 12x + 5y – 17 = 0

c) Giả sử ∆ có PTTQ: \(ax + by + c = 0\)

Ta có: \(D(0;4) \in \Delta  \Rightarrow 4b + c = 0 \Leftrightarrow c =  - 4b\)\( \Rightarrow \Delta :ax + by - 4b = 0\)

Ta có: \(d(I,\Delta ) = R \Leftrightarrow \frac{{\left| { - 2a + 3b - 4b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\)\( \Leftrightarrow \left| { - 2a - b} \right| = 2\sqrt {{a^2} + {b^2}} \)

                           \( \Leftrightarrow 4{a^2} + 4ab + {b^2} = 4({a^2} + {b^2}) \Leftrightarrow 3{b^2} = 4ab \Leftrightarrow \left[ \begin{array}{l}b = 0\\3b = 4a\end{array} \right.\)

Với b = 0, chọn a = 1 \( \Rightarrow \Delta \) có PT: x = 0

Với 3b = 4a, chọn a = 3, b = 4 \( \Rightarrow \Delta \) có PT: 3x + 4y – 16 = 0

Bài 56 trang 89 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x + 2)² + (y − 4)² = 25 và điểm A(-1; 3).

a) Xác định vị trí tương đối của điểm A đối với đường tròn (C)

b) Đường thẳng d thay đổi đi qua A cắt đường tròn tại M và N. Viết phương trình đường thẳng d sao cho MN ngắn nhất

Lời giải:

a) (C) có tâm I(-2 ; 4) và bán kính R = 5

Ta có: \(\overrightarrow {IA}  = (1; - 1) \Rightarrow IA = \sqrt 2 \)

Có: \(IA = \sqrt 2  < R \Rightarrow \) Điểm A nằm bên trong đường tròn (C)

b) Theo giả thiết, d cắt (C) tại 2 điểm M, N thỏa mãn MN ngắn nhất \( \Leftrightarrow \) khoảng cách từ tâm I đến d lớn nhất

Gọi H là hình chiếu của I trên d. Ta có: \(IH \le IA\)

\( \Rightarrow \) IH đạt GTLN khi và chỉ khi H trùng với A

\( \Rightarrow IA \bot d\) \( \Rightarrow d\) nhận \(\overrightarrow {IA}  = (1; - 1)\) làm vectơ pháp tuyến nên có PT: x – y + 4 = 0

Bài 57 trang 90 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho các đường thẳng:

∆₁: x + y + 1 = 0,  ∆₂: 3x + 4y + 20 = 0,  ∆₃: 2x - y + 50 = 0

và đường tròn (C): (x + 3)² + (y −1)² = 9.

Xác định vị trí tương đối của các đường thẳng đã cho đối với đường tròn (C).

Lời giải:

(C) có tâm I(-3 ; 1) và bán kính R = 3

+) Xét ∆₁: x + y + 1 = 0

Ta có: \(d(I,{\Delta _1}) = \frac{{\left| { - 3 + 1 + 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2} < R\) \( \Rightarrow {\Delta _1}\) cắt đường tròn (C) tại 2 điểm

+) Xét ∆₂: 3x + 4y + 20 = 0

Ta có: \(d(I,{\Delta _2}) = \frac{{\left| {3.( - 3) + 4.1 + 20} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3 = R\) \( \Rightarrow {\Delta _2}\) tiếp xúc với đường tròn (C)

+ Xét ∆₃: 2x - y + 50 = 0

Ta có: \(d(I,{\Delta _3}) = \frac{{\left| {2.( - 3) - 1 + 50} \right|}}{{\sqrt {{2^2} + {{( - 1)}^2}} }} = \frac{{43\sqrt 5 }}{5} > R\) \( \Rightarrow {\Delta _3}\) và đường tròn (C) không giao nhau

Bài 58 trang 90 SBT Toán 10 - Cánh Diều

Trong mặt phẳng toạ độ Oxy, cho điểm M(1 ; 1) và đường thẳng : 3x + 4y + 3 = 0. Viết phương trình đường tròn (C), biết (C) có tâm M và đường thẳng ∆ cắt (C) tại hai điểm N, P thoả mãn tam giác MNP đều.

Lời giải:

Gọi H là hình chiếu của M lên đường thẳng ∆

Ta có: \(MH = d(M,\Delta ) = \frac{{\left| {3 + 4 + 3} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2\)

Theo giả thiết, ∆MNP đều \( \Rightarrow \widehat {MNH} = {60^0}\)

Xét \(\Delta MNH\) vuông tại H có \(MN = \frac{{MH}}{{\sin \widehat {MNH}}} = \frac{2}{{\sin {{60}^0}}} = \frac{{4\sqrt 3 }}{3}\)\( \Rightarrow R = \frac{{4\sqrt 3 }}{3}\)

Vậy (C) có PT: \({(x - 1)^2} + {(y - 1)^2} = \frac{{16}}{3}\)

Sachbaitap.com