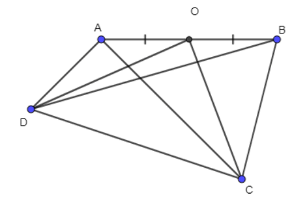
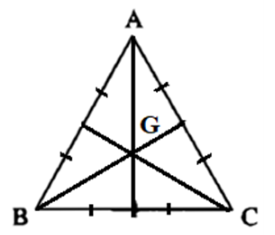
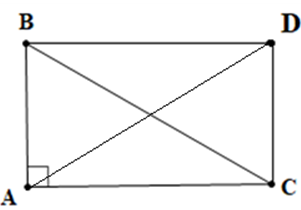
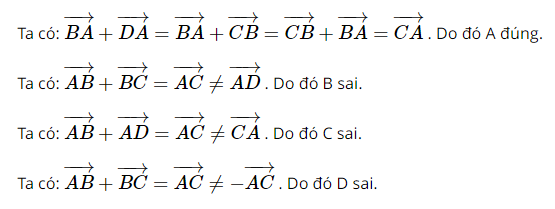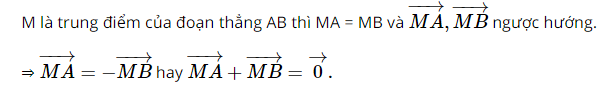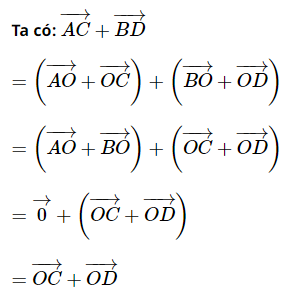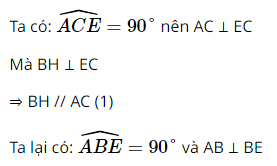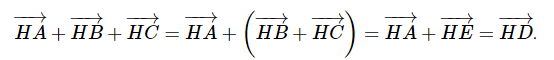Giải SBT Toán 10 trang 92, 93 Cánh Diều tập 1Giải bài 32, 33, 34, 35, 36, 37, 38, 39, 40 trang 92, bài 41, 42, 43, 44, 45, 46 trang 93 SBT Toán 10 Cánh Diều tập 1. Bài 33. Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây là đúng? Bài 32 trang 92 SBT Toán 10 - Cánh Diều Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng? A. \(\overrightarrow {MN} - \overrightarrow {NP} = \overrightarrow {MP} \) B. \( - \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \) C. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \) D. \(\overrightarrow {MN} + \overrightarrow {NP} = - \overrightarrow {MP} \) Lời giải: Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \) Chọn C Bài 33 trang 92 SBT Toán 10 - Cánh Diều Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây là đúng? A. \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \) B. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} \) C. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \) D. \(\overrightarrow {AB} + \overrightarrow {BC} = - \overrightarrow {AC} \) Lời giải: Đáp án đúng là A Bài 34 trang 92 SBT Toán 10 - Cánh Diều Cho các điểm A, B, O. Khẳng định nào sau đây là đúng? A. \(\overrightarrow {AB} = \overrightarrow {OA} - \overrightarrow {OB} \) B. \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \) C. \(\overrightarrow {AB} = \overrightarrow {OA} + \overrightarrow {OB} \) D. \(\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \) Lời giải: Với 3 điểm A, B, O ta có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \) Chọn B Bài 35 trang 92 SBT Toán 10 - Cánh Diều Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để điểm M là trung điểm của đoạn thẳng AB là: A. \(\overrightarrow {MA} = \overrightarrow {MB} \) B. \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\) C. \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng D. \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \) Lời giải: Đáp án đúng là D Vậy điều kiện đủ đề M là trung điểm của đoạn thẳng AB là Bài 36 trang 92 SBT Toán 10 - Cánh Diều Cho tam giác ABC. Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là: A. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} \) B. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \) C. \(\overrightarrow {GC} + \overrightarrow {GA} = \overrightarrow {GB} \) D. \(\overrightarrow {GA} + \overrightarrow {GB} - \overrightarrow {GC} = \overrightarrow 0 \) Lời giải: Ta có: Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) \( \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = - \overrightarrow {GA} \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = \ovaerrightarrow {AG} \) Chọn B Bài 37 trang 92 SBT Toán 10 - Cánh Diều Cho tứ giác ABCD, O là trung điểm của AB. Chứng minh \(\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AC} + \overrightarrow {BD} \)(*) Lời giải: Bài 38 trang 92 SBT Toán 10 - Cánh Diều Cho tam giác ABC vuông tại A, \(AB = 4a,AC = 5a\). Tính a) \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\) b) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) Lời giải: ∆ABC vuông tại A, \(AB = 4a,AC = 5a\) \( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt {41} \) a) Ta có: \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\sqrt {41} \) b) Dựng hình chữ nhật ABCD. Khi đó \(AD = BC = a\sqrt {41} \) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt {41} \) Bài 39 trang 92 SBT Toán 10 - Cánh Diều Cho tam giác đều ABC cạnh a. Tính: a) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right|\) b) \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\) c) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) Phương pháp: Bước 1: Lấy G là trọng tâm tam giác ABC Bước 2: Sử dụng quy tắc cộng, quy tắc trừ, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi và tính độ dài các vectơ tương ứng Lời giải: Gọi G là trọng tâm tam giác ABC Khi đó \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \), \(GA = GB = GC = \frac{{a\sqrt 3 }}{3}\) a) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\) b) Ta có: \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\) c) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\left( {\overrightarrow {GB} - \overrightarrow {GA} } \right) + \left( {\overrightarrow {GC} - \overrightarrow {GA} } \right)} \right| = \left| {\left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) - 2\overrightarrow {GA} } \right|\) (1) Lại có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = - \overrightarrow {GA} \) (2) Từ (1) và (2) suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| { - \overrightarrow {GA} - 2\overrightarrow {GA} } \right| = \left| { - 3\overrightarrow {GA} } \right| = 3\left| {\overrightarrow {GA} } \right| = 3GA = 3.\frac{{a\sqrt 3 }}{3} = a\sqrt 3 \) Bài 40 trang 92 SBT Toán 10 - Cánh Diều Cho tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\) (*). Chứng minh tam giác ABC vuông tại A. Phương pháp: Bước 1: Dựng hình bình hành ABDC Bước 2: Sử dụng quy tắc trừ hai vectơ và quy tắc hình bình hành để biến đổi giả thiết (*) Bước 3: Sử dụng dấu hiệu nhận biết hình chữ nhật để chứng minh tam giác ABC vuông tại A
Lời giải:
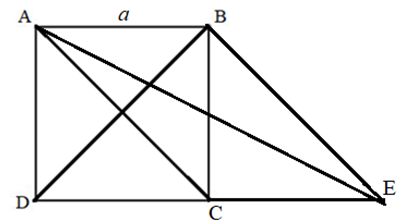
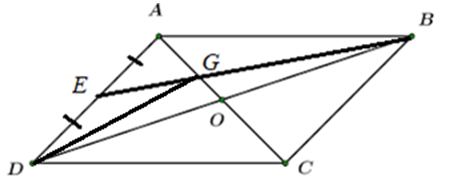
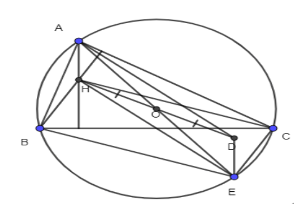
Dựng hình bình hành ABDC. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| \Leftrightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right| \Leftrightarrow AD = BC\) \( \Rightarrow \) Hình bình hành ABCD có hai đường chéo bằng nhau nên là hình chữ nhật \( \Rightarrow \widehat {BAC} = {90^0}\). Vậy tam giác ABC vuông tại A (ĐPCM) Bài 41 trang 93 SBT Toán 10 - Cánh Diều Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Chứng minh rằng nếu hai vectơ cùng hướng thì \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\) Lời giải: Lấy một điểm A trên mặt phẳng. Dựng \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) sao cho \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng \( \Rightarrow \left| {\overrightarrow a } \right| = AB,\left| {\overrightarrow b } \right| = BC\) Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow {AC} \) Lại có: AB + BC = AC \( \Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = AC = \left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\) (ĐPCM) Bài 42 trang 93 SBT Toán 10 - Cánh Diều Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) Lời giải: Dựng hình bình hành ABEC. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AE} \) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE\) Xét tam giác ADE vuông tại D có \(AE = \sqrt {A{D^2} + D{E^2}} = \sqrt {{a^2} + {{(2a)}^2}} = \sqrt {5{a^2}} = a\sqrt 5 \) Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = AE = a\sqrt 5 \) Bài 43 trang 93 SBT Toán 10 - Cánh Diều Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính: a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \) b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \) Lời giải: a) Do ABCD là hình bình hành nên O là trung điểm AC và BD \( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ,\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \) \(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \end{array}\) b) Xét tam giác ABD có AO và BE là hai đường trung tuyến cắt nhau tại G \( \Rightarrow \) G là trọng tâm ∆ABD \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow 0 \) Bài 44 trang 93 SBT Toán 10 - Cánh Diều Cho tam giác ABC. Tìm tập hợp các điểm M trong mặt phẳng thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC} - \overrightarrow {AM} } \right|\) Phương pháp: Sử dụng các quy tắc cộng, trừ 2 vectơ để biến đổi giả thiết rồi kết luận Lời giải: Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC} - \overrightarrow {AM} } \right| \Leftrightarrow \left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {MC} } \right| \Leftrightarrow AM = MC\) Vậy tập hợp các điểm M cần tìm là đường trung trực của đoạn thẳng AC Bài 45 trang 93 SBT Toán 10 - Cánh Diều Cho hai tam giác ABC và A’B’C’ có cùng trọng tâm là G. Chứng minh \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0 \) Phương pháp: Sử dụng tính chất trọng tâm tam giác, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} \) rồi kết luận Lời giải: Do G là trọng tâm tam giác ABC và tam giác A’B’C’ nên: \(\left\{ \begin{array}{l}\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} = \overrightarrow 0 \end{array} \right.\) Ta có: \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow {GA'} - \overrightarrow {GA} + \overrightarrow {GB'} - \overrightarrow {GB} + \overrightarrow {GC'} - \overrightarrow {GC} \) \( = \left( {\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} } \right) - \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)\)\( = \overrightarrow 0 - \overrightarrow 0 = \overrightarrow 0 \) (ĐPCM) Bài 46 trang 93 SBT Toán 10 - Cánh Diều Cho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác, D là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) Lời giải: Vẽ đường kính AE Mà CH ⊥ AB ⇒ BE // CH (2) Từ (1) và (2) suy ra BHEC là hình bình hành Xét tứ giác AHDE, có: O là trung điểm của HD (gt) O là trung điểm của AE Do đó AHDE là hình bình hành Khi đó, ta có:
Sachbaitap.com
Xem thêm tại đây:
Bài 4. Tổng và hiệu của hai vectơ
|
-

Giải SBT Toán 10 trang 99, 100 Cánh Diều tập 1
Giải bài 47, 48, 49, 50, 51 trang 99, bài 52, 53, 54, 55, 56 trang 100 SBT Toán 10 Cánh Diều tập 1. Bài 50. Cho đoạn thẳng AB và điểm C nằm giữa hai điểm A, B. Khẳng định nào sau đây là đúng?

 Tải ngay
Tải ngay