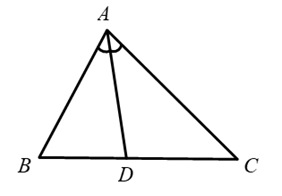
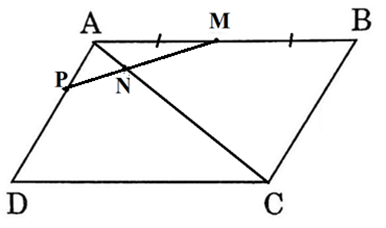
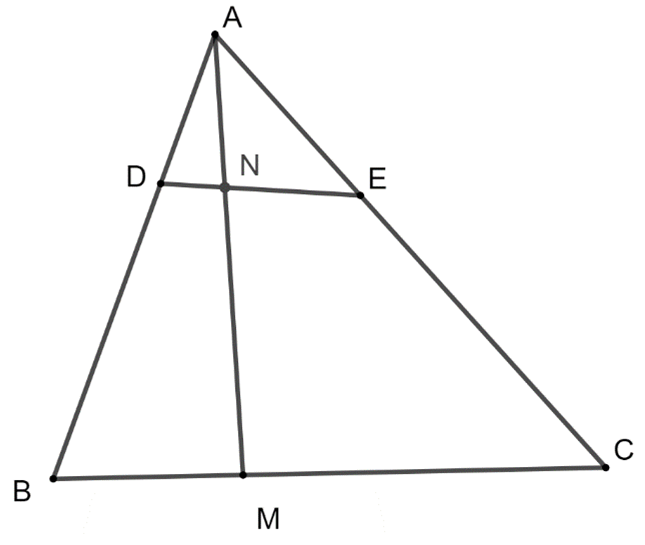
Giải SBT Toán 10 trang 99, 100 Cánh Diều tập 1Giải bài 47, 48, 49, 50, 51 trang 99, bài 52, 53, 54, 55, 56 trang 100 SBT Toán 10 Cánh Diều tập 1. Bài 50. Cho đoạn thẳng AB và điểm C nằm giữa hai điểm A, B. Khẳng định nào sau đây là đúng? Bài 47 trang 99 SBT Toán 10 - Cánh Diều Cho đoạn thẳng AB và O là trung điểm của AB. Khẳng định nào sau đây là đúng? A. \(\overrightarrow {AB} = 2\overrightarrow {OA} \) B. \(\overrightarrow {AB} = 2\overrightarrow {OB} \) C. \(\overrightarrow {AB} = - 2\overrightarrow {OB} \) D. \(\overrightarrow {AO} = 2\overrightarrow {AB} \) Lời giải: Đáp án đúng là B Bài 48 trang 99 SBT Toán 10 - Cánh Diều Cho tam giác ABC và M là trung điểm của BC, G là trọng tâm của tam giác. Khẳng định nào sau đây đúng? A. \(\overrightarrow {AM} = - 3\overrightarrow {GM} \) B. \(\overrightarrow {AM} = \frac{3}{2}\overrightarrow {GM} \) C. \(\overrightarrow {AM} = - \frac{3}{2}\overrightarrow {GM} \) D. \(\overrightarrow {AM} = 3\overrightarrow {GM} \) Lời giải: Đáp án đúng là D Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên ta có: Bài 49 trang 99 SBT Toán 10 - Cánh Diều Cho \(\overrightarrow a \ne \overrightarrow 0 \). Khẳng định nào sau đây là sai? A. \(\overrightarrow a \) và \(4\overrightarrow a \) cùng phương B. \(\overrightarrow a \) và \( - 4\overrightarrow a \) cùng phương C. \(\overrightarrow a \) và \(4\overrightarrow a \) không cùng hướng D. \(\overrightarrow a \) và \( - 4\overrightarrow a \) ngược hướng Lời giải: Đáp án đúng là C Bài 50 trang 99 SBT Toán 10 - Cánh Diều Cho đoạn thẳng AB và điểm C nằm giữa hai điểm A, B. Khẳng định nào sau đây là đúng? A. \(\overrightarrow {AC} = \frac{{AC}}{{AB}}\overrightararow {AB} \) B. \(\overrightarrow {AC} = - \frac{{AC}}{{AB}}\overrightarrow {AB} \) C. \(\overrightarrow {AC} = \frac{{AB}}{{AC}}\overrightarrow {AB} \) D. \(\overrightarrow {AC} = - \frac{{AB}}{{AC}}\overrightarrow {AB} \) Lời giải: Đáp án đúng là A Bài 51 trang 99 SBT Toán 10 - Cánh Diều Cho đoạn thẳng BC và điểm A nằm giữa hai điểm B, C. Khẳng định nào sau đây là đúng? A. \(\overrightarrow {AC} = \frac{{AC}}{{AB}}\overrightarrow {AB} \) B. \(\overrightarrow {AC} = - \frac{{AC}}{{AB}}\overrightarrow {AB} \) C. \(\overrightarrow {AC} = \frac{{AB}}{{AC}}\overrightarrow {AB} \) D. \(\overrightarrow {AC} = - \frac{{AB}}{{AC}}\overrightarrow {AB} \) Lời giải: Ta có: \(AC = \frac{{AC}}{{AB}}.AB\) mà A nằm giữa C và B nên \(\overrightarrow {AC} = - \frac{{AC}}{{AB}}.\overrightarrow {AB} \) Chọn B Bài 52 trang 100 SBT Toán 10 - Cánh Diều Cho tam giác ABC. Xác định các điểm M, N, P trong môi trường hợp sau: a) \(\overrightarrow {AM} = \overrightarrow {CB} \) b) \(\overrightarrow {AN} = - \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\) c) \(\overrightarrow {PA} - \overrightarrow {PB} + 2\overrightarrow {PC} = \overrightarrow 0 \) Lời giải: a) Theo giả thiết, \(\overrightarrow {AM} = \overrightarrow {CB} \)\( \Rightarrow \) \(\overrightarrow {AM} \) cùng hướng và có độ lớn bằng \(\overrightarrow {CB} \) Vậy điểm M thuộc đường thẳng đi qua A, song song với BC sao cho AMBC là hình bình hành b) Theo giả thiết, \(\overrightarrow {AN} = - \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\) Dựng hình bình hành ABDC, theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)\( \Rightarrow \overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AD} \) Vậy điểm N thuộc tia đối của tia AD thỏa mãn \(AN = \frac{1}{2}AD\) c) Theo giả thiết, \(\overrightarrow {PA} - \overrightarrow {PB} + 2\overrightarrow {PC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + 2\overrightarrow {PC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {PC} = - \frac{1}{2}\overrightarrow {BA} \) Dựng hình bình hành ABCD. Khi đó P là trung điểm của CD Vậy điểm P là trung điểm đoạn thẳng CD thỏa mãn ABCD là hình bình hành Bài 53 trang 100 SBT Toán 10 - Cánh Diều Cho tam giác ABC, kẻ phân giác AD. Đặt AB = c, AC = b. Chứng minh: \(b\overrightarrow {DB} + c\overrightarrow {DC} = \overrightarrow 0 \) (*) Phương pháp: Bước 1: Biểu diễn độ dài DB (hoặc DC) theo DC (hoặc DB) và xác định hướng các vectơ tương ứng Bước 2: Sử dụng định lí đường phân giác trong tam giác để biến đổi tỉ số độ dài \(\frac{{DB}}{{DC}}\) Bước 3: Biến đổi đẳng thức ở bước 1 rồi kết luận Lời giải: Ta có: \(DB = \frac{{DB}}{{DC}}.DC\) mà \(\overrightarrow {DB} \) và \(\overrightarrow {DC} \) ngược hướng \( \Rightarrow \overrightarrow {DB} = - \frac{{DB}}{{DC}}.\overrightarrow {DC} \)(1) Theo giả thiết, AD là đường phân giác của ∆ABC \( \Rightarrow \frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} = \frac{b}{c}\) (2) Từ (1) và (2) suy ra \(\overrightarrow {DB} = - \frac{c}{b}.\overrightarrow {DC} \Leftrightarrow b\overrightarrow {DB} = - c\overrightarrow {DC} \Leftrightarrow b\overrightarrow {DB} + c\overrightarrow {DC} = \overrightarrow 0 \) (ĐPCM) Bài 54 trang 100 SBT Toán 10 - Cánh Diều Cho hình bình hành ABCD. Lấy các điểm M, N, P thoả mãn \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} ,\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} \). Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \). Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {MN} ,\overrightarrow {NP} \) theo các vectơ \(\overrightarrow a ,\overrightarrow b \) và chứng minh ba điểm M, N, P thẳng hàng. Phương pháp: Bước 1: Xác định vị trí các điểm M, N, P trên các cạnh AB, AC, AD Bước 2: Sử dụng các quy tắc để biểu diễn các vectơ theo \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) Bước 3: Sử dụng điều kiện \(\overrightarrow {MN} = k\overrightarrow {NP} \) chứng minh M, N, P thẳng hàng. Lời giải: Theo giả thiết, M là trung điểm AB, N nằm giữa A và C, P nằm giữa A và D a) Ta có: + \(\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} \). Theo quy tắc hình bình hành, \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\) + \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} \)mà \(\overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\), \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} = \frac{1}{2}\overrightarrow a \) nên \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right) - \frac{1}{2}\overrightarrow a = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b \) + \(\overrightarrow {NP} = \overrightarrow {AP} - \overrightarrow {AN} \) mà \(\overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\), \(\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} = \frac{1}{3}\overrightarrow b \) nên \(\overrightarrow {NP} = \overrightarrow {AP} - \overrightarrow {AN} = \frac{1}{3}\overrightarrow b - \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right) = - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b \) Vậy \(\overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\); \(\overrightarrow {MN} = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b \); \(\overrightarrow {NP} = - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b \) b) Theo a, \(\overrightarrow {MN} = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b \); \(\overrightarrow {NP} = - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b \) \( \Rightarrow \overrightarrow {MN} = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b = \frac{3}{2}\left( { - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b } \right) = \frac{3}{2}\overrightarrow {NP} \) \( \Rightarrow \overrightarrow {MN} \) và \(\overrightarrow {NP} \) cùng phương. Vậy 3 điểm M, N, P thẳng hàng. Bài 55 trang 100 SBT Toán 10 - Cánh Diều Cho tam giác ABC. Lấy các điểm D, E, M, N thoả mãn \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {AE} = \frac{2}{5}\overrightarrow {AC} ,\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} ,\overrightarrow {AN} = k\overrightarrow {AM} \) với k là số thực. Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {DE} ,\overrightarrow {EN} \) theo các vectơ \(\overrightarrow a = \overrightarrow {AB} ,\overrightarrow b = \overrightarrow {AC} \) và tìm k để ba điểm D, E, N thẳng hàng. Lời giải: Theo giả thiết D, E, M, N nằm giữa 2 đầu mút các cạnh tương ứng AB, AC, BC, AM a) Ta có: \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow a \); \(\overrightarrow {AE} = \frac{2}{5}\overrightarrow {AC} = \frac{2}{5}\overrightarrow b \); \(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \Leftrightarrow \overrightarrow {AM} - \overrightarrow {AB} = \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AM} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \) + \(\overrightarrow {AN} = k\overrightarrow {AM} = k\left( {\frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b } \right) = \frac{{2k}}{3}\overrightarrow a + \frac{k}{3}\overrightarrow b \) + \(\overrightarrow {DE} = \overrightarrow {AE} - \overrightarrow {AD} = - \frac{1}{3}\overrightarrow a + \frac{2}{5}\overrightarrow b \) + \(\overrightarrow {EN} = \overrightarrow {AN} - \overrightarrow {AE} = k\left( {\frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b } \right) - \frac{2}{5}\overrightarrow b = \frac{{2k}}{3}\overrightarrow a + \frac{{5k - 6}}{{15}}\overrightarrow b \) b) D, E, N thẳng hàng khi và chỉ khi \(\overrightarrow {EN} = t\overrightarrow {DE} \) \( \Leftrightarrow \frac{{2k}}{3}\overrightarrow a + \frac{{5k - 6}}{{15}}\overrightarrow b = t\left( { - \frac{1}{3}\overrightarrow a + \frac{2}{5}\overrightarrow b } \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}\frac{{2k}}{3} = - \frac{t}{3}\\\frac{{5k - 6}}{{15}} = \frac{{2t}}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{3}k + \frac{1}{3}t = 0\\\frac{1}{3}k - \frac{2}{5}t = \frac{2}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \frac{6}{{17}}\\t = - \frac{{12}}{{17}}\end{array} \right.\) Vậy với \(k = \frac{6}{{17}}\) thì D, E, N thẳng hàng. Bài 56 trang 100 SBT Toán 10 - Cánh Diều Cho tam giác ABC. Lấy các điểm A', B', C' không trùng với đỉnh của tam giác và lần lượt thuộc các cạnh AB, BC, CA thoả mãn \(\frac{{AA'}}{{AB}} = \frac{{BB'}}{{BC}} = \frac{{CC'}}{{CA}}\). Chứng minh hai tam giác ABC và A'B'C' có cùng trọng tâm. Lời giải: Gọi G là trọng tâm tam giác ABC, G’ là trọng tâm tam giác A’B’C’. Khi đó \(\left\{ \begin{array}{l}\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} = \overrightarrow 0 \end{array} \right.\) Xét \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow {AG} + \overrightarrow {GG'} + \overrightarrow {G'A'} + \overrightarrow {BG} + \overrightarrow {GG'} + \overrightarrow {G'B'} + \overrightarrow {CG} + \overrightarrow {GG'} + \overrightarrow {G'C'} \) \( = \left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) + \left( {\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} } \right) + 3\overrightarrow {GG'} = 3\overrightarrow {GG'} \) (1) Mặt khác, đặt \(\frac{{AA'}}{{AB}} = \frac{{BB'}}{{BC}} = \frac{{CC'}}{{CA}} = k \Rightarrow \left\{ \begin{array}{l}AA' = kAB\\BB' = kBC\\CC' = kCA\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AA'} = k\overrightarrow {AB} \\\overrightarrow {BB'} = k\overrightarrow {BC} \\\overrightarrow {CC'} = k\overrightarrow {CA} \end{array} \right.\) (2) Từ (1) và (2) suy ra \(3\overrightarrow {GG'} = k\overrightarrow {AB} + k\overrightarrow {BC} + k\overrightarrow {CA} = k\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right) = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {GG'} = \overrightarrow 0 \) Do đó G và G’ trùng nhau. Vậy hai tam giác ABC và A'B'C' có cùng trọng tâm. Sachbaitap.com
Xem thêm tại đây:
Bài 5. Tích của một số với một vectơ
|
-

Giải SBT Toán 10 trang 105, 106 Cánh Diều tập 1
Giải bài 57, 58, 59, 60, 61 trang 105, bài 62, 63, 64, 65, 66 trang 106 SBT Toán 10 Cánh Diều tập 1. Bài 57. Cho tam giác ABC. Giá trị của biểu thức (overrightarrow {BA} .overrightarrow {CA} ) bằng:

 Tải ngay
Tải ngay