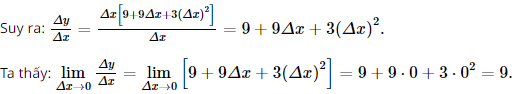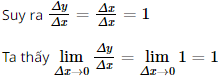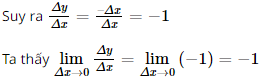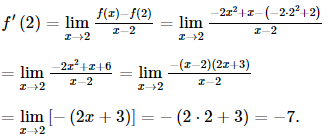Giải SGK Toán 11 Cánh Diều tập 2 trang 63Giải bài 1, 2, 3, 4 trang 63 SGK Toán lớp 11 Cánh Diều tập 2. a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên. b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được Bài 1 trang 63 SGK Toán 11 - Cánh Diều tập 2 Tính đạo hàm của hàm số \(f(x) = 3{x^3} - 1\) tại điểm \({x_0} = 1\) bằng định nghĩa Phương pháp: Sử dụng định nghĩa đạo hàm để tính đạo hàm Lời giải: Xét ∆x là số gia của biến số tại điểm x0 = 1. Ta có ∆y = f(1 + ∆x) – f(1) = 3(1 + ∆x)3 – 1 – (3.13 – 1) = 3 + 9∆x + 9.(∆x)2 + 3(∆x)3 – 1 – 2 = 9∆x + 9.(∆x)2 + 3(∆x)3 = ∆x[9 + 9∆x + 3(∆x)2]. Bài 2 trang 63 SGK Toán 11 - Cánh Diều tập 2 Chứng minh rằng hàm số \(f(x) = \left| x \right|\) không có đạo hàm tại điểm \({x_0} = 0\), nhưng có đạo hàm tại mọi điểm \(x \ne 0\) Phương pháp: Tách \(f(x) = \left| x \right|\) thành 2 phần và tìm đạo hàm của từng phần. Lời giải: Xét ∆x là số gia của biến số tại điểm x0 = 0. Ta có ∆y = f(0 + ∆x) – f(0) = |∆x| – |0| = |∆x|.
⦁ Với x > 0 ta có hàm số f(x) = x. Xét ∆x là số gia của biến số tại điểm x > 0. Ta có ∆y = f(x + ∆x) – f(x) = (x + ∆x) – x = ∆x.
Do đó với x > 0 thì hàm số có đạo hàm f’(x) = 1. ⦁ Với x < 0 ta có hàm số f(x) = –x. Xét ∆x là số gia của biến số tại điểm x < 0. Ta có ∆y = f(x + ∆x) – f(x) = – (x + ∆x) + x = –∆x.
Do đó với x < 0 thì hàm số có đạo hàm f’(x) = –1. Vậy hàm số f(x) = |x| không có đạo hàm tại x0 = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0. Bài 3 trang 63 SGK Toán 11 - Cánh Diều tập 2 Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C). a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6) Phương pháp: Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\): \(y = {k_0}(x - {x_0}) + {y_0}\) Lời giải: a) Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 có hệ số góc là:
Vậy hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 là f’(x) = –7. b) Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; – 6) là: y = –7(x – 2) – 6 hay y = –7x + 8. Bài 4 trang 63 SGK Toán 11 - Cánh Diều tập 2 Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là \(C(Q) = {Q^2} + 80Q + 3500\) a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên. b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được c) Hãy tính chi phí sản xuất máy vô tuyến thứ 100. Phương pháp: Áp dụng quy tắc tính đạo hàm bằng định nghĩa để tính Lời giải: a) Xét ∆Q là số gia của biến số tại điểm Q. Ta có ∆C = C(Q + ∆Q) – C(Q) = (Q + ∆Q)2 + 80(Q + ∆Q) + 3 500 – Q2 – 80Q – 3 500 = (∆Q)2 + 2Q. ∆Q + 80∆Q. = ∆Q(∆Q + 2Q + 80).
Vậy hàm chi phí biên là: C’(Q) = 2Q + 80 (USD). b) Ta có C’(90) = 2 . 90 + 80 = 260 (USD). Ý nghĩa: Để sản xuất thêm 1 sản phẩm từ 90 lên 91 sản phẩm cần chi phí biên (chi phí gia tăng) là 260 (USD) Sachbaitap.com
Xem thêm tại đây:
Bài 1. Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm
|
-

Giải SGK Toán 11 Cánh Diều tập 2 trang 71, 72
Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 71, 72 SGK Toán lớp 11 Cánh Diều tập 2.Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu ({v_0} = 196m/s) (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. (lấy (g = 9,8m/{s^2}))

 Tải ngay
Tải ngay