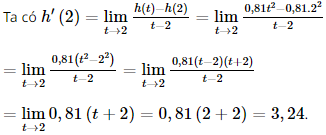Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 41Giải bài 1, 2, 3, 4, 5, 6 trang 41 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức: Bài 1 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2 Dùng định nghĩa để tính đạo hàm của các hàm số sau: a) \(f\left( x \right) = - {x^2}\); b) \(f\left( x \right) = {x^3} - 2x\); c) \(f\left( x \right) = \frac{4}{x}\). Phương pháp: Tính giới hạn \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\). Lời giải: a) Với bất kì x0 ∈ ℝ, ta có:
b) Với bất kì x0 ∈ ℝ, ta có:
c) Với bất kì x0 ≠ 0, ta có:
Bài 2 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hàm số \(f\left( x \right) = - 2{x^2}\) có đồ thị \(\left( C \right)\) và điểm \(A\left( {1; - 2} \right) \in \left( C \right)\). Tính hệ số góc của tiếp tuyến với \(\left( C \right)\) tại điểm \(A\). Phương pháp: Hệ số góc: \(f'\left( {{x_0}} \right)\). Lời giải: Hệ số góc của tiếp tuyến với (C) tại điểm A là:
Vậy hệ số góc của tiếp tuyến với (C) tại điểm A là −4. Bài 3 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2 Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3}\) a) Tại điểm \(\left( { - 1;1} \right)\); b) Tại điểm có hoành độ bằng 2. Phương pháp: Hệ số góc: \(f'\left( {{x_0}} \right)\). Phương trình tiếp tuyến: \(y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\). Lời giải: Ta có: (x3)′=3x2. a) Vì điểm M(−1; 1) không thuộc đồ thị hàm số (C) nên không có phương trình tiếp tuyến tại điểm M(−1; 1). b) Với x0=2⇔y0=23=8. Do đó N(2;8). Tiếp tuyến của (C) tại điểm N(2;8) có hệ số góc là: f′(2)=3.22=12. Phương trình tiếp tuyến của (C) tại điểm N là: y–8=12(x−2)⇔y=12x–24+8⇔y=12x–16. Bài 4 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2 Một chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = 4{t^3} + 6t + 2\), trong đó \(s\) tính bằng mét và \(t\) là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại \(t = 2\). Phương pháp: Vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) là: \(v\left( {{t_0}} \right) = s'\left( {{t_0}} \right)\) Lời giải: Vận tốc tức thời của chuyển động tại t = 2 là:
Vậy vận tốc tức thời của chuyển động lúc t = 2 là v(2) = 54 m/s. Bài 5 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2 Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức: a) Lãi kép với kì hạn 6 tháng; b) Lãi kép liên tục. Phương pháp: a) Sử dụng công thức \(T = A.{\left( {1 + \frac{r}{n}} \right)^n}\). b) Sử dụng công thức \(T = A.{e^{rt}}\). Lời giải: a) Nếu tiền lãi được tính theo thể thức lãi kép với kì hạn 6 tháng. Tổng số tiền vốn và lãi người đó nhận được sau 1 năm là:
Vậy tổng số tiền vốn và lãi người đó nhận được sau 1 năm là 10 506 250 đồng, nếu tiền lãi được tính theo thể thức lãi kép với kì hạn 6 tháng. b) Nếu tiền lãi được tính theo thể thức lãi kép liên tục. Tổng số tiền vốn và lãi người đó nhận được sau 1 năm là:
Vậy tổng số tiền vốn và lãi người đó nhận được sau 1 năm là 10 512 711 đồng, nếu tiền lãi được tính theo thể thức lãi kép liên tục. Bài 6 trang 41 SGK Toán 11 - Chân trời sáng tạo tập Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức: a) Lãi kép với kì hạn 6 tháng; b) Lãi kép liên tục. Phương pháp: a) Sử dụng công thức \(T = A.{\left( {1 + \frac{r}{n}} \right)^n}\). b) Sử dụng công thức \(T = A.{e^{rt}}\). Lời giải:
Vậy vận tốc tức thời của chuyển động lúc t = 2 là v(2) = h' (2) = 3,24 m/s. Sachbaitap.com
Xem thêm tại đây:
Bài 1. Đạo hàm
|
-

Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 48, 49
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 48, 49 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,8 t2, trong đó t là thời gian được tính bằng giây và \({\rm{s}}\) tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm \(t = 2\) sau khi thả vật đó, tính:

 Tải ngay
Tải ngay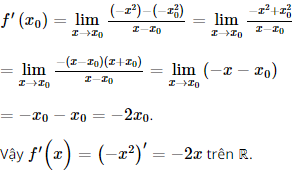
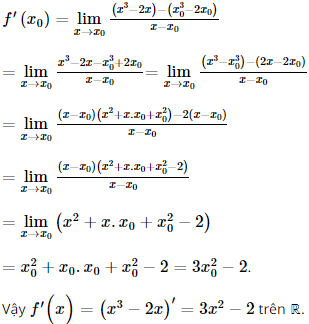
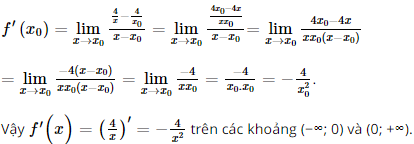
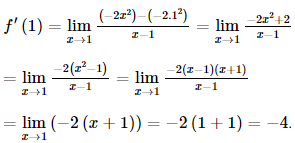
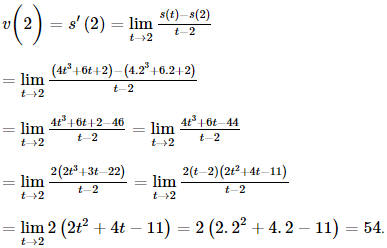
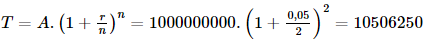
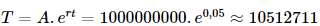 (đồng).
(đồng).