Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 48, 49Giải bài 1, 2, 3, 4, 5, 6, 7 trang 48, 49 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,8 t2, trong đó t là thời gian được tính bằng giây và \({\rm{s}}\) tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm \(t = 2\) sau khi thả vật đó, tính: Bài 1 trang 48 SGK Toán 11 - Chân trời sáng tạo tập 2 Tính đạo hàm của các hàm số sau: a) \(y = 2{{\rm{x}}^3} - \frac{{{x^2}}}{2} + 4{\rm{x}} - \frac{1}{3}\); b) \(y = \frac{{ - 2{\rm{x}} + 3}}{{{\rm{x}} - 4}}\); c) \(y = \frac{{{x^2} - 2{\rm{x}} + 3}}{{{\rm{x}} - 1}}\); d) \(y = \sqrt {5{\rm{x}}} \). Phương pháp: Áp dụng đạo hàm của tổng, hiệu, tích thương. Lời giải:
Bài 2 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2 Tính đạo hàm của các hàm số sau: a) \(y = \sin 3x\); b) \(y = {\cos ^3}2x\); c) \(y = {\tan ^2}x\); d) \(y = \cot \left( {4 - {x^2}} \right)\). Phương pháp: Sử dụng công thức tính đạo hàm của hàm hợp: \(y{'_x} = y{'_u}.u{'_x}\). Lời giải: a) y' = (sin3x)' = cos3x×(3x)' = 3cos3x. b) y' = (cos32x)' = 3cos22x(cos2x)' = −6cos22xsin2x. c) y' = (tan2x)' = 2tanx×(tanx)' d) y' = [cot(4 – x2)]' = Bài 3 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2 Tính đạo hàm của các hàm số sau: a) \(y = \left( {{x^2} - x} \right){.2^x}\); b) \(y = {x^2}{\log _3}x\); c) \(y = {e^{3x + 1}}\). Phương pháp: a) b) Sử dụng đạo hàm của tổng, hiệu, tích thương. c) Sử dụng công thức tính đạo hàm của hàm hợp: \(y{'_x} = y{'_u}.u{'_x}\). Lời giải: a) y' = [(x2 – x)×2x]' = (x2 – x)'×2x + (x2 – x)×(2x)' = (2x – 1)×2x + (x2 – x)×2x×ln2 = 2x(x2ln2 + 2x – 1 – xln2). b) y' = (x2log3x)' = (x2)'log3x + x2(log3x)' = 2xlog3x + c) y' = (e3x + 1)' = e3x + 1×(3x + 1)' = 3e3x + 1. Bài 4 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2 Tính đạo hàm cấp hai của các hàm số sau: a) \(y = 2{x^4} - 5{x^2} + 3\); b) \(y = x{e^x}\). Phương pháp: Tính \(y'\), sau đó tính y''. Lời giải: a) y' = (2x4 – 5x2 + 3)' = 8x3 – 10x. y" = (8x3 – 10x)' = 24x2 – 10. Vậy y" = 24x2 – 10. b) y' = (xex)' = x'ex + x×(ex)' = ex + xex. y" = (ex + xex)' = ex + ex + xex = 2ex + xex. Vậy y" = 2ex + xex. Bài 5 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2 Cân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số \(w\left( t \right) = 0,000758{t^3} - 0,0596{t^2} + 1,82t + 8,15\), trong đó \(t\) được tính bằng tháng và \(w\) được tính bằng pound (nguồn: https://www.cdc.gov/growthcharts/data/who/GrChrt_Boys). Tính tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi. Phương pháp: Tính \({\rm{w}}'\left( {10} \right)\). Lời giải: Tốc độ thay đổi cân nặng của bé gái đó tại thời điểm t là: w'(t) = (0,000758t3 – 0,0596t2 + 1,82t + 8,15)' = 0,002274t2 – 0,1192t + 1,82. Tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi là: w'(10) = 0,002274×(10)2 – 0,1192×10 + 1,82. = 0,8554 (pound/tháng). Vậy tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi là 0,8554 pound/tháng. Bài 6 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2 Một công ty xác định rằng tổng chi phí của họ, tính theo nghìn đô-la, để sản xuất \(x\) mặt hàng là \(C\left( x \right) = \sqrt {5{x^2} + 60} \) và công ty lên kế hoạch nâng sản lượng trong \(t\) tháng kể từ nay theo hàm số \(x\left( t \right) = 20t + 40\). Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó? Phương pháp: Tính \(C'\left( t \right)\) với \(t = 4\). Lời giải: Ta có Có x'(t) = (20t + 40)' = 20; x(4) = 120. Khi đó, tốc độ tăng chi phí của công ty sau t tháng là: C'(x(t)) = C'(x)×x'(t). Tốc độ tăng chi phí của công ty sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó là: C'(x(4)) = C'(120)×x'(4) = Tốc độ tăng chi phí của công ty sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó khoảng 44,7 nghìn đô/tháng. Bài 7 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2 Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức \(s\left( t \right) = 0,81{t^2}\), trong đó \(t\) là thời gian được tính bằng giây và \({\rm{s}}\) tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm \(t = 2\) sau khi thả vật đó, tính: a) Quãng đường vật đã rơi; b) Gia tốc của vật. Phương pháp: a) Tính \(s\left( 2 \right)\). b) Tính a(2) = s''(2). Lời giải: a) Quãng đường vật đã rơi tại thời điểm t = 2 là: s(2) = 0,81×22 = 3,24 (m). Vậy sau 2 giây vật đã rơi được 3,24 m. b) Có v(t) = s'(t) = (0,81t2)' = 1,62t. a(t) = v'(t) = (1,62t)' = 1,62. Vậy gia tốc của vật tại thời điểm t = 2 là 1,62 m/s2. Sachbaitap.com
Xem thêm tại đây:
Bài 2. Các quy tắc tính đạo hàm
|
-

Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 51, 52
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 trang 51, 52 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Dân số P (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức, trong đó t là thời gian được tính bằng năm. Tìm tốc độ tăng dân số tại thời điểm t = 12.

 Tải ngay
Tải ngay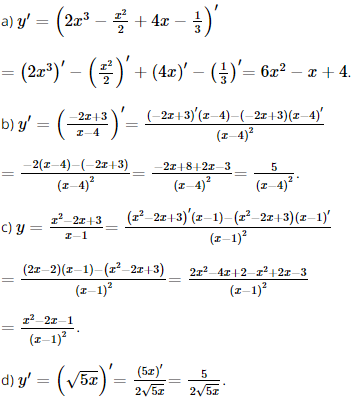
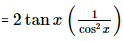 = 2tanx(1 + tan2x).
= 2tanx(1 + tan2x).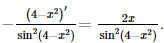
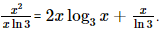
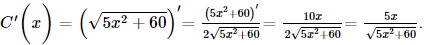
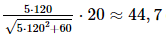 (nghìn đô-la/tháng).
(nghìn đô-la/tháng).