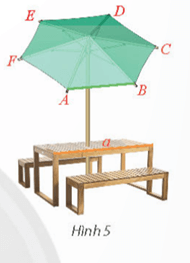
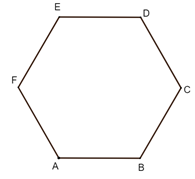
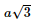Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 56Giải bài 1, 2, 3, 4, 5, 6 trang 56 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5). Tính số đo góc hợp bởi đường thẳng a lần lượt với các đường thẳng AF, AE. Bài 1 trang 56 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\). Phương pháp: Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). Lời giải:
Vì CD // AB nên (SB, CD) = (SB, AB) = Xét tam giác SBA có: SA ⊥AB nên ΔSAB vuông tại A.
Mặt khác, CB // AD nên (SD, CB) = (SD, AD) = Xét tam giác SDA có: SD ⊥ AD nên ΔSDA vuông tại D.
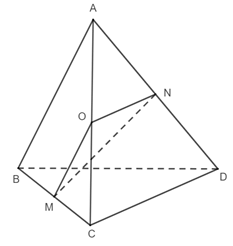
Bài 2 trang 56 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\). Phương pháp: Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). Lời giải:
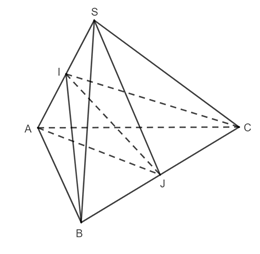
Gọi a là độ dài cạnh của tứ diện đều ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AC, BC và AD. Xét tam giác ABC: M là trung điểm của AC. N là trung điểm của BC. Nên MN là đường trung bình của tam giác ABC. ⇒ MN // AB; MN = Tương tự: MP là đường trung bình tam giác ACD: ⇒ MP // CD; MP = Từ (1) và (2) ⇒ MN = MP = Tam giác ABD đều có BP là trung tuyến nên BP = Tam giác ACD đều có CP là trung tuyến nên CP = Xét tam giác BCP có: BP = CP = ⇒ Tam giác BCP cân tại P. Mà N là trung điểm của BC ⇒ PN là đường trung tuyến nên PN ⊥ CN PN = Xét tam giác MNP: MP2 + MN2 = ⇒ MP2 + MN2 = PN2 ⇒ Tam giác MNP vuông tại M. Ta có: (AB, CD) = (MN, MP) = Vậy AB ⊥ CD. Bài 3 trang 56 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {BSA} = \widehat {CSA} = {60^ \circ },\) \(\widehat {BSC} = {90^ \circ }\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \bot SA\) và \(IJ \bot BC\). Phương pháp: Để chứng minh hai đường thẳng vuông góc, ta chứng minh góc giữa chúng bằng \({90^ \circ }\). Lời giải:
Xét tam giác SAB có: SA = SB = a
⇒ Tam giác SAB đều. Mà I là trung điểm của SA ⇒ IB = Xét tam giác SAC có: SA = SC = a
⇒ Tam giác SAC đều. Mà I là trung điểm của SA ⇒ IC = Ta có BSC là tam giác vuông cân tại S.
Xét tam giác ABC: AB = AC = a AB2 + AC2 = a2 + a2 = 2a2 BC2 = ⇒ AB2 + AC2 = BC2 ⇒ Tam giác ABC vuông cân tại A. Mà J là trung điểm đoạn BC ⇒ AJ ⊥ BC
Xét tam giác SBC vuông cân tại S: Mà J là trung điểm đoạn BC ⇒ SJ ⊥ BC
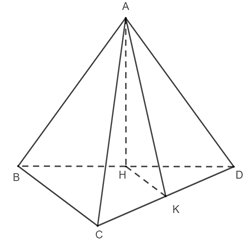
Xét tam giác JSA: AJ = SJ = ⇒ Tam giác JSA cân tại J. Mà I là trung điểm của SA ⇒ IJ là đường trung tuyến của tam giác JSA. hay IJ ⊥SA. Xét tam giác IBC: IB = IC = ⇒ Tam giác IBC cân tại I. Mà J là trung điểm của BC ⇒ IJ là đường trung tuyến của tam giác IBC. hay IJ ⊥BC. Bài 4 trang 56 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thẳng \(AK\) và \(BC\). Phương pháp: Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). Lời giải:
Gọi H là trung điểm của BD. Ta có: K là trung điểm của CD. Nên HK là đường trung bình tam giác BCD ⇒ HK // BC; HK = ⇒ (AK, BC) = (AK, HK) Xét tam giác ABC đều có H là trung điểm của BC ⇒ AH = Xét tam giác ACD đều có K là trung điểm của CD ⇒ AK = Xét tam giác AHK: ⇒ Vậy (AK, BC) = Bài 5 trang 56 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(BC\) và \(A{\rm{D}}\). Biết \(AB = CD = 2a\) và \(MN = a\sqrt 3 \). Tính góc giữa \(AB\) và \(C{\rm{D}}\). Phương pháp: Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). Lời giải:
Gọi O là trung điểm của AC. ⇒ OM là đường trung bình tam giác ABC ⇒ OM // AB; OM = Tương tự ON là đường trung bình tam giác ACD. ⇒ ON // CD; ON = ⇒ (AB, CD) = (OM, ON) Trong tam giác MON: OM = ON = a; MN =
Bài 6 trang 56 SGK Toán 11 - Chân trời sáng tạo tập 2 Một ô che nắng có viền khung hình lục giác đều \(ABCDEF\) song song với mặt bàn và có cạnh \(AB\) song song với cạnh bàn \(a\) (Hình 5). Tinh số đo góc hợp bởi đường thẳng \(a\) lần lượt với các đường thẳng \(AF,AE\) và \(A{\rm{D}}\).
Phương pháp: Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). Lời giải:
Ta có: AB // a, nên (a, AF) = (AB, AF) = 120° (a, AE) = (AB, AE) = 90° (a, AD) = (AB, AD) = 60° Sachbaitap.com
Xem thêm tại đây:
Bài 1. Hai đường thẳng vuông góc
|
-

Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 64
Giải bài 1, 2, 3, 4, 5 trang 64 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng, có các cạnh bên đều bằng 2a. a) Tính góc giữa SC và AB. b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng.

 Tải ngay
Tải ngay
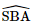
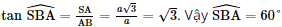
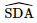
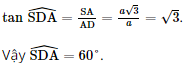

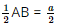
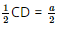
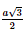
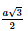
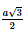
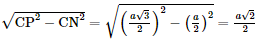
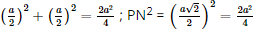
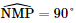
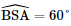
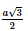
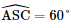
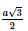
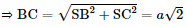
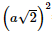 =2a2
=2a2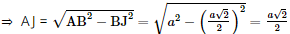
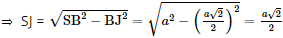
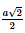
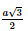
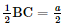
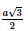
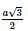
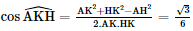
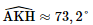
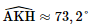
 AB = a
AB = a CD = a
CD = a