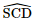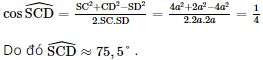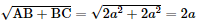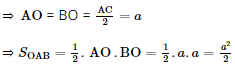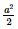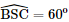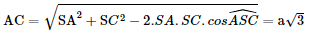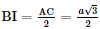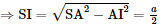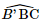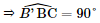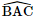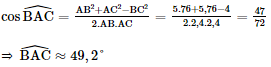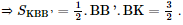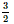Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 64Giải bài 1, 2, 3, 4, 5 trang 64 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng, có các cạnh bên đều bằng 2a. a) Tính góc giữa SC và AB. b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng. Bài 1 trang 64 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Cho biết \(ABCD\) là hình thang vuông tại \(A\) và \({\rm{D}}\), \(AB = 2AD\). a) Chứng minh \(CD \bot \left( {SAD} \right)\). b) Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(CM \bot \left( {SAB} \right)\). Phương pháp: Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng. Lời giải:
a) Ta có: b) Ta có: AB // CD ⇒ AM // CD AM = CD ⇒ AMCD là hình bình hành Mà
Bài 2 trang 64 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình vuông \(ABCD\). Gọi \(H,K\) lần lượt là trung điểm của \(AB,AD\). Trên đường thẳng vuông góc với \(\left( {ABCD} \right)\) tại \(H\), lấy điểm \(S\). Chứng minh rằng: a) \(AC \bot \left( {SHK} \right)\); b) \(CK \bot \left( {SDH} \right)\). Phương pháp: Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng. Lời giải:
a) Xét tam giác ADB: H là trung điểm AB K là trung điểm AD ⇒ HK là đường trung bình của ΔADB.
Ta có:
b) Gọi I=CK ∩ DH Xét ΔAHD và ΔDKC: AH = DK
AD = CD ⇒ ΔAHD = ΔDKC (c.g.c)
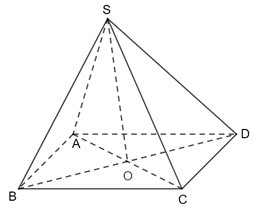
Mà SH ⊥ (ABCD) ⇒ SH ⊥ CK Vậy CK ⊥ (SDH). Bài 3 trang 64 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(a\sqrt 2 \), có các cạnh bên đều bằng \(2a\). a) Tính góc giữa \(SC\) và \(AB\). b) Tính diện tích hình chiếu vuông góc của tam giác \(SAB\) trên mặt phẳng \(\left( {ABCD} \right)\). Phương pháp: a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). b) Sử dụng phép chiếu vuông góc. Lời giải:
a) Ta có: AB // CD ⇒">⇒⇒ (SC, AB) = (SC, CD) = Xét ΔSCD , áp dụng định lí cos, ta có :
b) Gọi O=AC∩BD">O = AC ∩ BD Ta có: ΔSAC cân tại S nên SO ⊥ AC (1) ΔSBD cân tại S nên SO ⊥ BD (2) Từ (1) và (2) suy ra SO ⊥ (ABCD) Do đó O là hình chiếu vuông góc của S lên (ABCD). Mà A, B ∈ (ABCD) Vậy ΔOAB là hình chiếu vuông góc của ΔSAB lên (ABCD). Ta có: AC = Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.
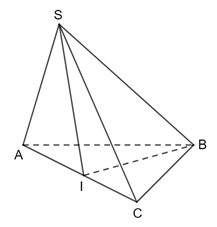
Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là Bài 4 trang 64 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {ASB} = 90^\circ ,\widehat {BSC} = {60^ \circ }\) và \(\widehat {ASC} = {120^ \circ }\). Gọi \(I\) là trung điểm cạnh \(AC\). Chứng minh \(SI \bot \left( {ABC} \right)\). Phương pháp: Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng. Lời giải:
Tam giác SBC cân tại S (vì SB = SC = a ) có Suy ra ΔSBC đều nên BC = a Áp dụng định lí Pythagore vào ΔSAB vuông tại S , ta có :
Áp dụng định lí cos vào ΔSAC , ta có:
Ta có: AB2 + BC2 = AC2 nên ΔABC vuông tại B (theo định lí Pythagore đảo) . Lại có I là trung điểm AC nên ΔSAC cân tại S mà I là trung điểm của AC nên SI ⊥ AC (1)
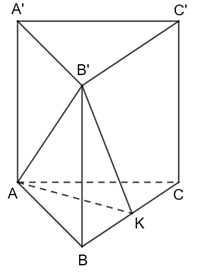
Ta có: SI2 + IB2 = SB2 nên ΔSBI vuông tại I (theo định lí Pythagore đảo) . Suy ra SI ⊥ IB (2) Từ (1) và (2) suy ra SI ⊥ (ABC) Bài 5 trang 64 SGK Toán 11 - Chân trời sáng tạo tập 2 Một cái lều có dạng hình lăng trụ \(ABC.A'B'C'\) có cạnh bên \(AA'\)vuông góc với đáy (Hình 24). Cho biết \(AB = AC = 2,4m;BC = 2{\rm{ }}m;AA' = 3m\). a) Tính góc giữa hai đường thẳng \(AA'\) và \(BC\); \(A'B'\) và \(AC\). b) Tính diện tích hình chiếu vuông góc của tam giác \(ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\). Phương pháp: a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\). Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\). b) Sử dụng phép chiếu vuông góc. Lời giải:
a) + Vì AA′ // BB ′ nên (AA′, BC) = (BB′, BC) = Ta có: AA ′ ⊥ (ABC), AA′ // BB ′ ⇒ BB ′ ⊥ (ABC) hay BB ′ ⊥ BC
+ Vì A′B′ // AB nên (A ′B′, AC) = (AB, AC) = ΔABC có: b) Kẻ AK ⊥ BC. Mà AA ′ ⊥ (ABC), AA ′ // BB′ ⇒ BB ′ ⊥ (ABC) ⇒ BB ′ ⊥ AK (1) Ta có: AK ⊥ BC; BC // B′C' ⇒ AK ⊥ B′C′ (2) Từ (1) và (2) ⇒ AK ⊥ (BB′C′C) ⇒ K là hình chiếu vuông góc của A trên (BB ′ C ′ C) Mà B, B ′ ∈ (BB ′ C ′ C) Vậy ΔKBB ′ là hình chiếu vuông góc của ΔABB ′ lên (BB ′C′C ). Ta có: ΔABC cân tại A có AK ⊥ BC K là trung điểm của BC
Vậy diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB′CC′ ) là Sachbaitap.com
Xem thêm tại đây:
Bài 2. Đường thẳng vuông góc với mặt phẳng
|
-

Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 73, 74
Giải bài 1, 2, 3, 4, 5, 6 trang 73, 74 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp.

 Tải ngay
Tải ngay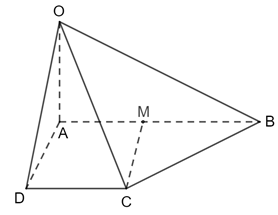
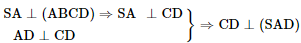
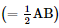
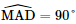 ⇒ AMCD là hình chữ nhật.
⇒ AMCD là hình chữ nhật.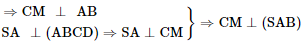
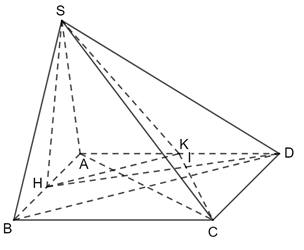

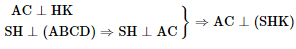
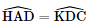
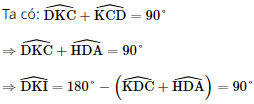 ⇒ DH ⊥ CK
⇒ DH ⊥ CK