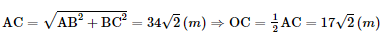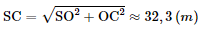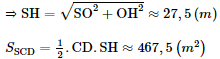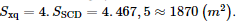Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 73, 74Giải bài 1, 2, 3, 4, 5, 6 trang 73, 74 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp. Bài 1 trang 73 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(C\), mặt bên \(SAC\) là tam giác đều và nằm trong mặt phẳng vuông góc với \(\left( {ABC} \right)\). a) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SAC} \right)\). b) Gọi \(I\) là trung điểm của \(SC\). Chứng minh rằng \(\left( {ABI} \right) \bot \left( {SBC} \right)\). Phương pháp: Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng. Lời giải:
a) Ta có (SAC) ⊥ (ABC) ⇒ AC ⊥ (ABC) ⇒ AC ⊥ BC Mà (SAC) ∩ (ABC) = AC nên BC ⊥ (SAC) Do đó (SBC) ⊥ (SAC). b) Ta có: BC ⊥ (SAC) nên BC ⊥ AI (AI ⊂ (SAC)) (1) Tam giác SAC đều có I là trung điểm của SC nên AI ⊥ SC (2) Từ (1) và (2) suy ra AI ⊥ (SBC) Mà AI ⊂ (ABI) nên (ABI) ⊥ (SAC) Bài 2 trang 73 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho tam giác đều \(ABC\) cạnh \(a\), \(I\) là trung điểm của \(BC\), \(D\) là điểm đối xứng với \(A\) qua \(I\). Vẽ đoạn thẳng \(S{\rm{D}}\) có độ dài bằng \(\frac{{a\sqrt 6 }}{2}\) và vuông góc với \(\left( {ABC} \right)\). Chứng minh rằng: a) \(\left( {SBC} \right) \bot \left( {SAD} \right)\); b) \(\left( {SAB} \right) \bot \left( {SAC} \right)\). Phương pháp: Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng. Lời giải:
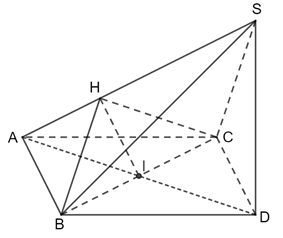
a) Tam giác ABC đều có I là trung điểm nên AI ⊥ CB hay AD ⊥ BC. Vì SD ⊥ (ABC) ⇒ SD ⊥ BC. ⇒ BC ⊥ (SAD) Nên (SAD) ⊥ (SBC) b) Tam giác ABC đều nên AI=a33,AD=a3">AI= Ta có: ΔSAD vuông tại D nên Kẻ IH ⊥ SA. Xét ΔAHI và ΔADS:
Do đóΔAHI ᔕ ΔADS (g.g)
Tam giác BHC có HI là trung tuyến và HI = ⇒ ΔBHC vuông tại H. Ta có: BC ⊥ (SAD) nên SA ⊥ BC. Mà SA ⊥ HI nên SA ⊥ (HBC)
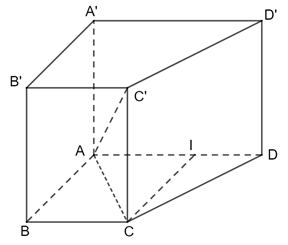
Mà HB ⊂ (SAB) ⇒ (SAB) ⊥ (SAC) Bài 3 trang 73 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AA' = 2a,AD = 2a,AB = BC = a\). a) Tính độ dài đoạn thẳng \(AC'\). b) Tính tổng diện tích các mặt của hình lăng trụ. Phương pháp: Sử dụng định lí Pitago. Lời giải:
Vậy độ dài đoạn thẳng AC′ là
Gọi I là trung điểm của AD. Khi đó ABCI là hình vuông nên IC = IB = IA = Xét tam giác ICD vuông cân tại I:
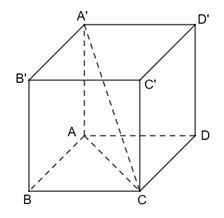
Tổng diện tích các mặt của hình lăng trụ là Vậy tổng diện tích các mặt của hình lăng trụ là: S= Bài 4 trang 74 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình hộp đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi. Cho biết \(AB = BD = a,A'C = 2a\). a) Tính độ dài đoạn thẳng \(AA'\). b) Tính tổng diện tích các mặt của hình hộp. Phương pháp: Sử dụng định lí Pitago. Lời giải:
a) Xét tam giác ABD có: AB = AD = BD = a nên ΔABD đều
Xét tam giác ABC có: AA′ ⊥ (ABCD) ⇒ AA′ ⊥ AC ⇒ ΔAA′C vuông tại A. Vậy độ dài đoạn thẳng AA′ là: AA′=a b) Ta có:
Tổng diện tích các mặt của hình hộp là:
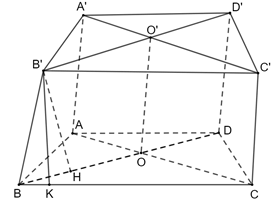
Vậy tổng diện tích các mặt của hình hộp là Bài 5 trang 74 SGK Toán 11 - Chân trời sáng tạo tập 2 Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ và đường nối tâm hai đáy bằng \(a\). Tính độ dài cạnh bên và đường cao của mỗi mặt bên. Phương pháp: Sử dụng định lí Pitago. Lời giải:
Gọi OO' là đường nối tâm của hai đáy. Kẻ B′H ⊥ BD (H BD), B′K ⊥ BC (K ∈ BC). Ta có:
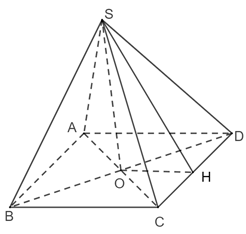
Vì OO′B′H là hình chữ nhật nên OH=B′= Do đó BH = BO = OH • ΔBB′H vuông tại H nên • BCC′B′ là hình thang cân nên • ΔBB′K vuông tại K nên Bài 6 trang 74 SGK Toán 11 - Chân trời sáng tạo tập 2 Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp. Phương pháp: Sử dụng định lí Pitago. Lời giải:
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều S.ABCD có O là tâm của đáy. Kẻ SH ⊥ CD (H ∈ CD) Ta có: SO = 21,6 m , AD = 34 m
ΔSOC vuông tại O ⇒ Do đó độ dài cạnh bên bằng 32,3 m. Tam giác SCD cân tại S ⇒ SH vừa là trung tuyến, vừa là đường cao của tam giác SCD ⇒ H là trung điểm của CD. Mà O là trung điểm của AD. ⇒ OH là đường trung bình của tam giác ACD ⇒ OH = Ta có: SO ⊥ (ABCD) SO ⊥ OH ⇒ ΔSOH vuông tại O.
Diện tích xung quanh của kim tự tháp là:
Vậy độ dài cạnh bênlà 32,3 m và diện tích xung quanh của kim tự tháp là 1870 m2. Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hai mặt phẳng vuông góc
|
-

Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 81, 82
Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 81,82 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Tính thể tích của khối chóp cụt lục giác đều (ABCDEF.{rm{ }}A'B'C'D'E'F') với (O) và (O') là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là (a) và (frac{a}{2},OO' = a).

 Tải ngay
Tải ngay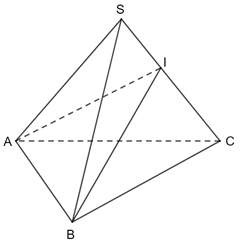
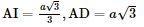
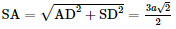
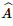 chung
chung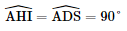
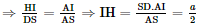
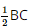
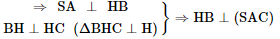
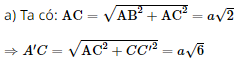
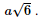
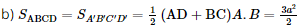
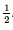 AD = a
AD = a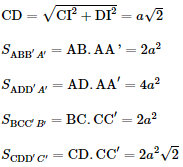
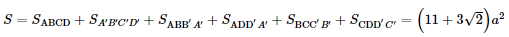
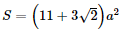
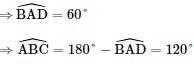
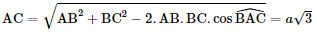
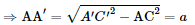
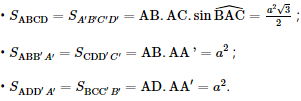
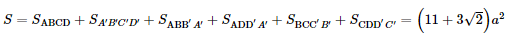
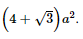
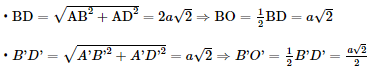
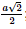
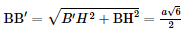 (theo định lí Pythagore).
(theo định lí Pythagore).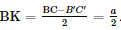
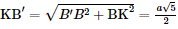 (theo định lí Pythagore)
(theo định lí Pythagore)