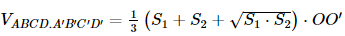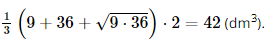Giải SGK Toán 11 Kết nối tri thức tập 2 trang 63Giải bài 7.28, 7.29, 7.30, 7.31, 7.32 trang 63 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a. Bài 7.28 trang 63 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a. Phương pháp: Thế tích khối chóp \(V = \frac{1}{3}h.S\) Lời giải:
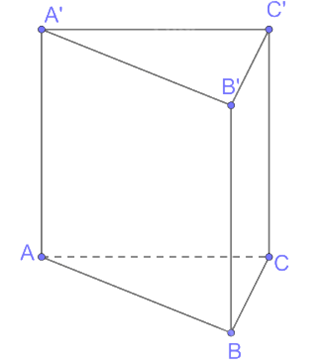
Gọi G là hình chiếu của S trên mặt phẳng (ABC). Vì S.ABC là khối chóp đều nên G là trọng tâm của tam giác ABC. Có SG ⊥ (ABC). Giả sử AG ∩ BC tại D, khi đó D là trung điểm của BC, AD ⊥ BC. Xét tam giác ABC đều cạnh a, AD là đường cao nên AD = Vì AG = Xét tam giác SGA vuông tại G, có SG = Ta có Khi đó thể tích khối tứ diện đều có cạnh bằng a là: Bài 7.29 trang 63 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho khối lăng trụ đứng ABC.A'B'C' có AA' = 5 cm, AB = 6 cm, BC = 2 cm, \(\widehat {ABC} = {150^0}.\) Tính thể tích của khối lăng trụ. Phương pháp: Thể tích khối lăng trụ \(V = h.S\) Lời giải:
Vì ABC.A'B'C' là khối lăng trụ đứng nên A'A ⊥">⊥⊥ (ABC). Có
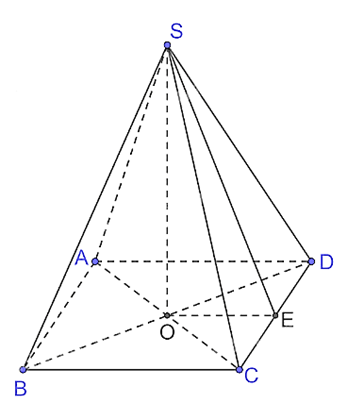
Bài 7.30 trang 63 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau. a) Cạnh bên tạo với mặt đáy một góc bằng \({60^0}.\) b) Mặt bên tạo với mặt đáy một góc bằng \({45^0}.\) Phương pháp: - Thế tích khối chóp \(V = \frac{1}{3}h.S\) - Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó. - Góc giữa hai mặt phẳng là góc giữa 2 đường thẳng trong hai mặt phẳng vuông góc với giao tuyến tại cùng một điểm. Lời giải:
Gọi O là giao điểm của AC và BD. Do S.ABCD là khối chóp đều nên SO ⊥">⊥⊥ (ABCD). Khi đó OC là hình chiếu của SC trên mặt phẳng (ABCD). Khi đó góc giữa cạnh bên SC và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng OC và SC, mà (OC, SC) = Xét tam giác ABC vuông tại B, có AC = Vì ABCD là hình vuông nên O là trung điểm của AC, suy ra OC = Xét tam giác SOC vuông tại O, có SO = OC . tan60° = Khi đó b)
Kẻ OE ⊥ CD tại E. Vì SO ⊥ (ABCD) nên SO ⊥ CD mà OE ⊥ CD nên CD ⊥ (SOE), suy ra CD ^ SE.Khi đó góc giữa hai mặt phẳng (SCD) và (ABCD) bằng góc giữa hai đường thẳng OE và SE, mà (OE, SE) = Xét tam giác SOE vuông tại O, có nên tam giác SOE vuông cân tại O, suy ra SO = OE. Xét tam giác BCD, có OE // BC (vì cùng vuông góc với CD), mà O là trung điểm của BD nên E là trung điểm của CD, do đó OE là đường trung bình của tam giác BCD. Suy ra OE = Vậy Bài 7.31 trang 63 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.
Phương pháp:
Thể tích khối lăng trụ \(V = h.S\)
Lời giải:
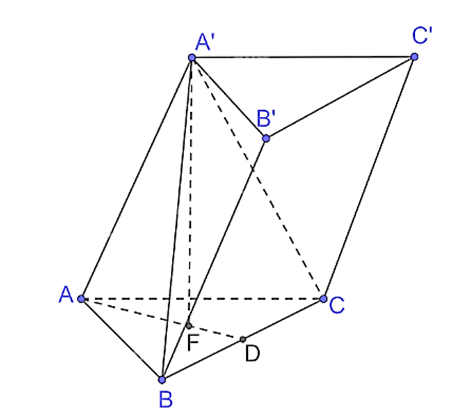 Vì hình chóp A'.ABC có A'A = A'B = A'C, ABC là tam giác đều nên hình chóp A'.ABC là hình chóp đều. Gọi F là hình chiếu của A' trên mặt phẳng (ABC), khi đó F là trọng tâm tam giác ABC. Khi đó A ⊥ (ABC) hay A'F là đường cao của hình lăng trụ ABC.A'B'C'. Giả sử AF ∩ CB tại D, suy ra D là trung điểm của BC, AD ⊥ BC. Vì ABC là tam giác đều cạnh a, đường cao AD nên AD = Có AF = Xét tam giác A'FA vuông tại F, có A'F = Khi đó Bài 7.32 trang 63 SGK Toán 11 - Kết Nối Tri Thức tập 2 Từ một tấm tôn hình vuông có cạnh 8dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp) như Hình 7.99.
b) Tính cạnh bên của thùng. c) Hỏi thùng có thể chứa được nhiều nhất bao nhiêu lít nước? Phương pháp:
a) Có AB // A'B' nên AB // (A'B'C'D'). AD // A'D' nên AD // (A'B'C'D'). Do đó (ABCD) // (A'B'C'D'). Vì bác Hùng cắt bỏ bốn phần như nhau ở bốn góc và hàn lại sẽ tạo thành 4 mặt bên là các hình thang cân. Vậy chiếc thùng có dạng hình chóp cụt. b) Dựa vào hình 7.99, ta có A'B' = B'C' = C'D' = D'A' = 8 – 2 = 6 (dm). Kẻ AH ⊥ A'B' tại H, Kẻ BK ⊥ A'B' tại K. Khi đó ABKH là hình chữ nhật, suy ra AB = HK = 3 dm, AH = BK = (8 – 3) : 2 = 2,5 dm. Xét ∆AHA' và ∆BKB' có AA' = BB', Do đó ∆AHA' = ∆BKB', suy ra A'H = B'K = (A'B' – HK): 2 = (6 – 3) : 2 = 1,5 dm. Xét tam giác AHA' vuông tại H, có AA' = Vậy cạnh bên của thùng là c) Gọi O và O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'. Vì ACC'A' là hình thang cân nên đường cao của hình chóp cụt cũng chính là đường cao của hình thang cân. Kẻ CE ⊥ A'C' tại E. Vì OCEO' là hình chữ nhật nên OC = O'E. Xét tam giác ABC vuông tại B có AC = Mà O là trung điểm của AC nên OC = Xét tam giác A'B'C' vuông tại B' có A'C' = Mà O' là trung điểm của A'C' nên O'C' = Có C'E = O'C' – O'E =
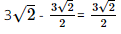 dm dmXét tam giác CC'E vuông tại E, có CE = Ta có S1 = SABCD = 3 . 3 = 9 (dm2); S2 = SA'B'C'D' = 6 . 6 = 36 (dm2). Khi đó: = Ta có 42 dm3 = 42 lít. Vậy thùng có thể chứa được nhiều nhất là 42 lít nước. Sachbaitap.com
Xem thêm tại đây:
Bài 27. Thể tích
|
-
Giải SGK Toán 11 Kết nối tri thức tập 2 trang 64, 65
Giải bài 7.33, 7.34, 7.35, 7.36, 7.37, 7.38, 7.39, 7.40, 7.41, 7.42, 7.43, 7.44, 7.45 trang 63 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và (OA = a,OB = asqrt 2 ) và (OC = 2a). Tính khoảng cách từ điểm (O) đến mặt phẳng ((ABC)).

 Tải ngay
Tải ngay
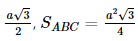
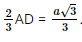
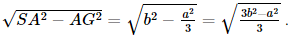
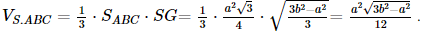
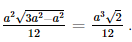
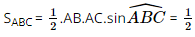 .6.2.sin150o = 3(cm2).
.6.2.sin150o = 3(cm2).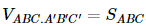 .AA' = 3 . 5 = 15 (cm3).
.AA' = 3 . 5 = 15 (cm3).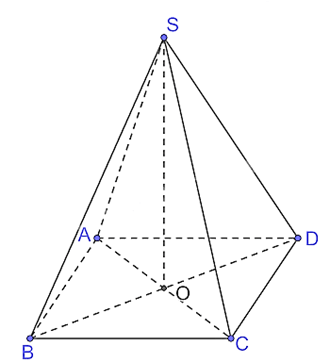
 = 60o
= 60o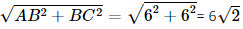 (cm).
(cm).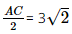 (cm).
(cm).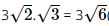 (cm).
(cm).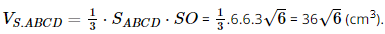
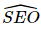 = 45o.
= 45o.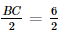

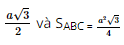
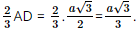
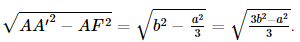
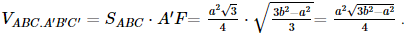
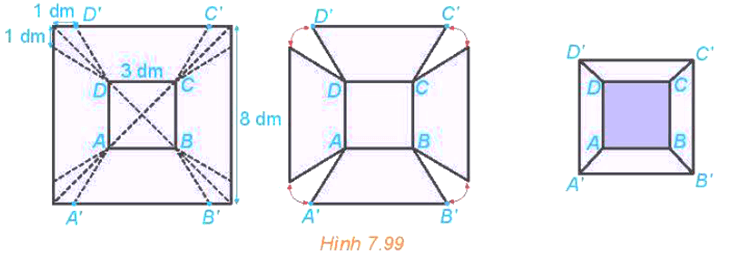 a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.
a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.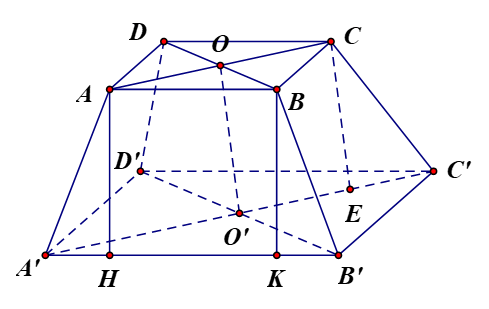
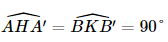
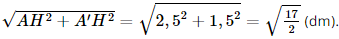
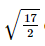
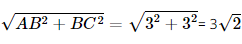 dm.
dm.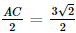 dm.
dm.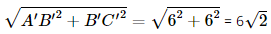 dm.
dm.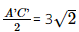 dm
dm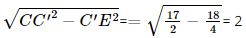 dm
dm