Giải SGK Toán 11 Kết nối tri thức tập 2 trang 79Giải bài 8.16, 8.17, 8.18, 8.19, 8.20, 8.21, 8.22, 8.23, 8.24, 8.25 trang 79 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Một đoàn khách du lịch gồm 31 người, trong đó có 7 người đến từ Hà Nội, 5 người đến từ Hải Phòng. Chọn ngẫu nhiên một người trong đoàn. Tính xác suất để người đó đến từ Hà Nội hoặc đến từ Hải Phòng. Bài 8.16 trang 79 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi A là biến cố "Rút được tấm thẻ ghi số chẵn lớn hơn 9"; B là biến cố "Rút được tấm thẻ ghi số không nhỏ hơn 8 và không lớn hơn 15". Số phần tử của \(A \cup B\) là A. 11. B. 10. C. 12. D. 13. Phương pháp: Cho A và B là hai biến cố. Biến cố: “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là \(A \cup B.\) Lời giải: Đáp án đúng là: A Ta có: A = {10; 12; 14; 16; 18; 20}. B = {8; 9; 10; 11; 12; 13; 14; 15}. Vậy A ∪ B = {8; 9; 10; 11; 12; 13; 14; 15; 16; 18; 20}. Bài 8.17 trang 79 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi A là biến cố "Rút được tấm thẻ ghi số chẵn lớn hơn 9"; B là biến cố "Rút được tấm thẻ ghi số không nhỏ hơn 8 và không lớn hơn 15". Số phần tử của AB là A. 5. B. 6. C. 3. D. 4. Phương pháp: Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu AB. Lời giải: Đáp án đúng là: C Ta có: A = {10; 12; 14; 16; 18; 20} B = {8; 9; 10; 11; 12; 13; 14; 15} Vậy AB = A ∩ B = {10; 12; 14}. Bài 8.18 trang 79 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tại một hội thảo quốc tế có 50 nhà khoa học, trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người trong hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp là A. \(\frac{{47}}{{50}}.\) B. \(\frac{{37}}{{50}}.\) C. \(\frac{{39}}{{50}}.\) D. \(\frac{{41}}{{50}}.\) Phương pháp: Công thức cộng xác suất \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\) Lời giải: Đáp án đúng là: A Gọi A là biến cố “Người được chọn thành thạo tiếng Anh”; B là biến cố “Người được chọn thành thạo tiếng Pháp”. Biến cố: “Người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp” là biến cố hợp của A và B. Khi đó P(A) = Ta có: P(A ∪ B) = P(A) + P(B) – P(AB) = Vậy xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là Bài 8.19 trang 79 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tại một hội thảo quốc tế có 50 nhà khoa học, trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người trong hội thảo. Xác suất để người được chọn không thành thạo cả hai thứ tiếng Anh hay Pháp là A. \(\frac{7}{{50}}.\) B. \(\frac{3}{{50}}.\) C. \(\frac{9}{{50}}.\) D. \(\frac{{11}}{{50}}.\) Phương pháp: Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: Đáp án đúng là: B Gọi E là biến cố “Người được chọn không thành thạo cả hai thứ tiếng Anh hay Pháp”. Khi đó, Ta có: Do đó, P(E) = 1 – P( Vậy xác suất để người được chọn không thành thạo cả hai thứ tiếng Anh hay Pháp là Bài 8.20 trang 79 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một lớp có 40 học sinh, trong đó có 23 học sinh thích bóng chuyền, 18 học sinh thích bóng rổ, 26 học sinh thích bóng chuyền hoặc bóng rổ hoặc cả hai. Chọn ngẫu nhiên một học sinh trong lớp. Xác suất để chọn được học sinh không thích cả bóng chuyền và bóng rổ là A. \(\frac{{9}}{{20}}.\) B. \(\frac{{7}}{{20}}.\) C. \(\frac{{19}}{{40}}.\) D. \(\frac{{21}}{{40}}.\) Phương pháp: Công thức cộng xác suất \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\) Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: Đáp án đúng là: B Số học sinh thích cả bóng chuyền và bóng rổ là: 23 + 18 – 26 = 15 (học sinh) Gọi A là biến cố “Học sinh thích bóng chuyền”; B là biến cố “Học sinh thích bóng rổ”; E là biến cố “Học sinh không thích cả bóng chuyền và bóng rổ”. Khi đó P(A) = P( ) = P(A ∪ B) = P(A) + P(B) – P(AB) = Suy ra: P(E) = 1 – P( Vậy xác suất để chọn được học sinh không thích cả bóng chuyền và bóng rổ là Bài 8.21 trang 79 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một lớp có 40 học sinh, trong đó có 23 học sinh thích bóng chuyền, 18 học sinh thích bóng rổ, 26 học sinh thích bóng chuyền hoặc bóng rổ hoặc cả hai. Chọn ngẫu nhiên một học sinh trong lớp. Xác suất để chọn được học sinh thích bóng chuyền và không thích bóng rổ là A. \(\frac{7}{{40}}.\) B. \(\frac{9}{{40}}.\) C. \(\frac{1}{{5}}.\) D. \(\frac{{11}}{{40}}.\) Phương pháp: Tính xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\) Lời giải: Đáp án đúng là: C Số học sinh thích cả bóng chuyền và bóng rổ là: 23 + 18 – 26 = 15 (học sinh).
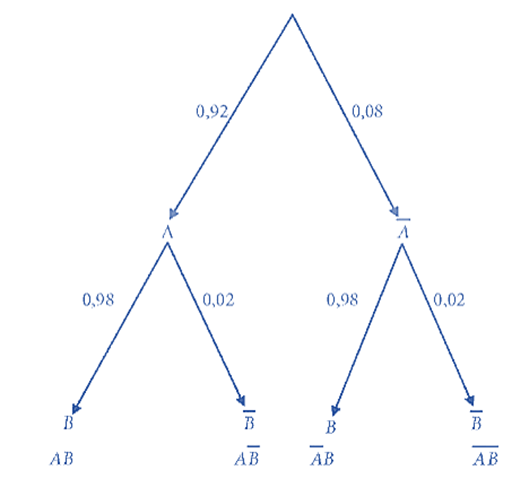
Số học sinh thích bóng chuyền và không thích bóng rổ là 23 – 15 = 8 (học sinh). Vậy xác suất để chọn được học sinh thích bóng chuyền và không thích bóng rổ là: Bài 8.22 trang 80 SGK Toán 11 - Kết Nối Tri Thức tập 2 Hai vận động viên bắn súng A và B mỗi người bắn một viên đạn vào tấm bia một cách độc lập. Xét các biến cố sau: M: “Vận động viên A bắn trúng vòng 10”; N: “Vận động viên B bắn trúng vòng 10”. Hãy biểu diễn các biến cố sau theo biến cố M và N C: “Có ít nhất một vận động viên bắn trúng vòng 10”; D: “Cả hai vận động viên bắn trúng vòng 10”; E: “Cả hai vận động viên đều không bắn trúng vòng 10”; F: “Vận động viên A bắn trúng và vận động viên B không bắn trúng vòng 10”; G: “Chỉ có duy nhất một vận động viên bắn trúng vòng 10”. Phương pháp: - Cho A và B là hai biến cố. Biến cố: “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là \(A \cup B.\) - Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu AB. Lời giải: Ta có: C = M ∪ N; D = MN; E = F = M G = Bài 8.23 trang 80 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một đoàn khách du lịch gồm 31 người, trong đó có 7 người đến từ Hà Nội, 5 người đến từ Hải Phòng. Chọn ngẫu nhiên một người trong đoàn. Tính xác suất để người đó đến từ Hà Nội hoặc đến từ Hải Phòng. Phương pháp: Tính xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\) Lời giải: Số cách chọn một người trong đoàn là: 31. Số người đến từ Hà Nội hoặc đến từ Hải Phòng là: 7 + 5 = 12. Vậy xác suất để người đó đến từ Hà Nội hoặc đến từ Hải Phòng là Bài 8.24 trang 80 SGK Toán 11 - Kết Nối Tri Thức tập 2 Gieo một con xúc xắc cân đối, đồng chất liên tiếp hai lần. Xét các biến cố sau: A: “Ở lần gieo thứ nhất, số chấm xuất hiện trên con xúc xắc là 1”; B: “Ở lần gieo thứ hai, số chấm xuất hiện trên con xúc xắc là 2” C: “Tổng số chấm xuất hiện trên con xúc xắc ở hai lần gieo là 8” D: “Tổng số chấm xuất hiện trên con xúc xắc ở hai lần gieo là 7”. Chứng tỏ rằng các cặp biến cố A và C; B và C, C và D không độc lập. Phương pháp: Với hai biến cố A và B, nếu \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) thì A và B không độc lập. Lời giải: Không gian mẫu là tập hợp số chấm xuất hiện khi gieo con xúc xắc hai lần liên tiếp khi đó n(Ω) = 6 . 6 = 36. A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6)}. Suy ra: P(A) = B = {(1; 2); (2; 2); (3; 2); (4; 2); (5; 2); (6; 2)}. Suy ra: P(B) = C = {(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)}. Suy ra: P(C) = D = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)}. Suy ra: P(D) = Do đó: P(A) . P(C) = P(B) . P(C) = P(C) . P(D) = Mặt khác: AC = ∅. Suy ra: P(AC) = 0. BC = {(6; 2)}. Suy ra: P(BC) = CD = ∅. Suy ra: P(CD) = 0 Khi đó: P(AC) ≠ P(A) . P(C) ; P(BC) ≠ P(B) . P(C); P(CD) ≠ P(C) . P(D). Vậy các cặp biến cố A và C; B và C; C và D không độc lập. Bài 8.25 trang 80 SGK Toán 11 - Kết Nối Tri Thức tập 2 Hai chuyến bay của hai hãng hàng không X và Y, hoạt động độc lập với nhau. Xác suất để chuyến bay của hãng X và hãng Y khởi hành đúng giờ tương ứng là 0,92 và 0,98. Dùng sơ đồ hình cây, tính xác suất để: a) Cả hai chuyến bay khởi hành đúng giờ, b) Chỉ có duy nhất một trong hai chuyến bay khởi hành đúng giờ, c) Có ít nhất một trong hai chuyến bay khởi hành đúng giờ. Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Gọi biến cố A: “Chuyến bay của hãng X khởi hành đúng giờ”, biến cố B: “Chuyến bay của hãng Y khởi hành đúng giờ”. Từ giả thiết, ta có hai biến cố A và B độc lập. Ta có sơ đồ hình cây để mô tả như sau:
Theo sơ đồ hình cây, ta có: a) P(AB) = P(A) . P(B) = 0,92 . 0,98 = 0,9016. Vậy xác suất để cả hai chuyến bay khởi hành đúng giờ là 0,9016. b) P( Vậy xác suất để chỉ có một chuyến bay khởi hành đúng giờ 0,0968. c) P( Suy ra P(A ∪ B) = 1 – P( Vậy xác suất để có ít nhất một trong hai chuyến bay khởi hành đúng giờ là 0,9984. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối chương 8
|

 Tải ngay
Tải ngay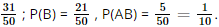 .
. .
.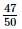
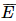 là biến cố “Người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp”.
là biến cố “Người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp”.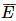 = A ∪ B.
= A ∪ B.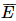 ) = 1 – P(A ∪ B) = 1 –
) = 1 – P(A ∪ B) = 1 – 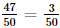 .
.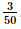
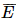 = A ∪ B.
= A ∪ B.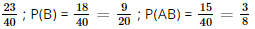 .
. .
.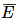 ) =
) = 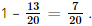 .
.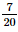
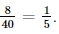
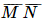 ;
;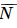 ;
;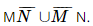
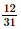
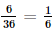 .
.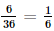 .
.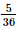 .
.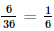 .
.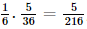 ;
;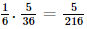 ;
;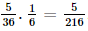 .
.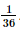 .
.
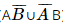 ) = P
) = P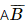 ) + P(
) + P(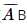 ) = 0,92 . 0,02 + 0,08 . 0,98 = 0,0968.
) = 0,92 . 0,02 + 0,08 . 0,98 = 0,0968.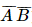 ) = 0,08 . 0,02 = 0,0016
) = 0,08 . 0,02 = 0,0016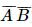 ) = 1 – 0,0016 = 0,9984.
) = 1 – 0,0016 = 0,9984.