Giải SGK Toán 11 trang 109 Cánh Diều tập 1Giải bài 1, 2, 3, 4 trang 109 SGK Toán lớp 11 Cánh Diều tập 1. Bài 1. Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao? Bài 1 trang 109 SGK Toán 11 tập 1 - Cánh Diều Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
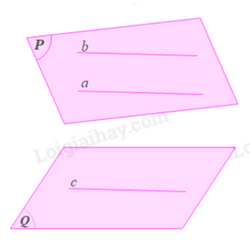
Phương pháp: Theo dấu hiệu nhận biết hai mặt phẳng song song: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q) Lời giải: Trường hợp a cắt b theo dấu hiệu nhận biết hai mặt phẳng song song thì ý kiến đúng Trường hợp a không cắt b thì a // b Ta có: a thuộc (P), a // (Q) B thuộc (P), b // (Q) Do đó: (P) // (Q) Vậy ý kiến đúng Bài 2 trang 109 SGK Toán 11 tập 1 - Cánh Diều
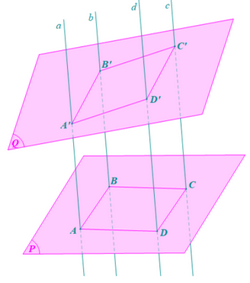
• Ta có: AB // CD (do ABCD là hình bình hành). Mà CD ⊂ mp(CDD’C’) nên AB // (CDD’C’). Lại có a // d nên A’A // D’D
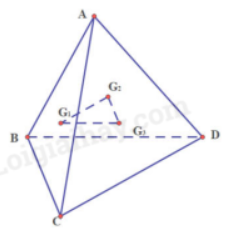
Mà D’D ⊂ mp(CDD’C’) nên A’A // (CDD’C’). Ta có: AB // (CDD’C’); A’A // (CDD’C’); AB, A’A cắt nhau tại A và cùng nằm trong (ABB’A’) Do đó (ABB’A’) // (CDD’C’). Ta có: (ABB’A’) // (CDD’C’); (ABB’A’) ∩ (Q) = A’B’; (CDD’C’) ∩ (Q) = C’D’. Do đó A’B’ // C’D’. • Tương tự, (ADD’A’) // (BCC’B); (ADD’A’) ∩ (Q) = A’D’; (BCC’B) ∩ (Q) = B’C’. Do đó A’D’ // B’C’. Tứ giác A’B’C’D’ có A’B’ // C’D’ và A’D’ // B’C’ nên A’B’C’D là hình bình hành. Bài 3 trang 109 SGK Toán 11 tập 1 - Cánh Diều Cho tứ diện ABCD. Lấy \({G_1},{G_2},{G_3}\)lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. a) Chứng minh rằng \(({G_1}{G_2}{G_3})//(BCD)\) b) Xác định giao tuyến của mặt phẳng \(({G_1}{G_2}{G_3})\) với mặt phẳng \((ABD)\) Phương pháp: Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải:
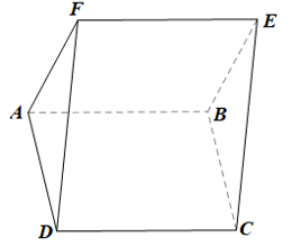
a) Gọi E, F, H là trung điểm của BC, CD, BD Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\) \({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\) Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\) Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\) Tương tự ta có:\({G_2}{G_3}//(BCD)\) Do đó, \({G_1}{G_2}{G_3}//(BCD)\) b) Ta có: \({G_1}{G_2}{G_3}//(BCD)\) nên \({G_1}{G_2} // BD\) mà \({G_3}\) là điểm chung của hai mặt phẳng Từ \({G_3}\) kẻ \({G_3}x\) sao cho \({G_3}x//BD\) Vậy \({G_3}x\) là giao tuyến cấn tìm Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. a) Chứng minh rằng (AFD) // (BEC) b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính \(\frac{{AN}}{{NC}}\) Phương pháp: Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q) Lời giải: a)
Ta có: BE // AF (do ABEF là hình bình hành); AF ⊂ (AFD) Do đó BE // (AFD). Ta cũng có: BC // AD (do ABCD là hình bình hành) AD ⊂ (AFD) Do đó BC // (AFD). Do BE // (AFD); BC // (AFD); BE, BC cắt nhau tại điểm B và cùng nằm trong mp(BEC) Suy ra (AFD) // (BEC). b) 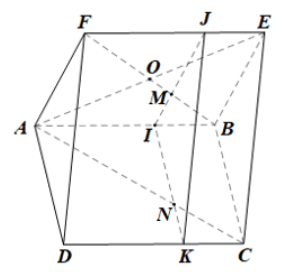 +) Do (AFD) song song với (P) nên tồn tại hai đường thẳng trong (AFD) song song với (P). • Trong mp(ABEF), qua điểm M vẽ đường thẳng song song với AF, đường thẳng này cắt AB, EF lần lượt tại I, J. Khi đó IJ // AF, mà AF ⊂ (AFD) nên IJ // (AFD). • Trong mp(ABCD), qua điểm I vẽ đường thẳng song song với AD, cắt CD tại K. Khi đó IK // AD, mà AD ⊂ (AFD) nên IK // (AFD). • Ta có: IJ // (AFD); IK // (AFD); IJ, IK cắt nhau tại điểm I và cùng nằm trong mp(IJK). Do đó (IJK) // (AFD). Mà M ∈ IJ, IJ ⊂ (IJK) nên mp (P) đi qua M và song song với (AFD) chính là mp(IJK). +) Trong mp(ABCD), AC cắt IK tại N, khi đó N là giao điểm của AC và (P).
Sachbaitap.com
Xem thêm tại đây:
Bài 4. Hai mặt phẳng song song
|
-

Giải SGK Toán 11 trang 113 Cánh Diều tập 1
Giải bài 1, 2, 3 trang 113 SGK Toán lớp 11 Cánh Diều tập 1. Bài 3. Cho hình lăng trụ tam giác ABC.A’B’C‘. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B‘.

 Tải ngay
Tải ngay