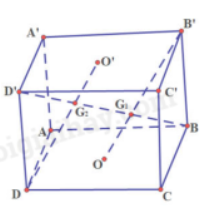
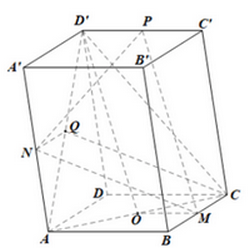
Giải SGK Toán 11 trang 113 Cánh Diều tập 1

Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều

Cho hình hộp ABCD.A’B’C’D’.

a) Chứng minh rằng (ACB’) // (A’C’D’)

b) Gọi\({G_1},{G_2}\)lần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D’).

Chứng minh rằng\({G_1},{G_2}\)lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.

c) Chứng minh rằng \(B{G_1} = {G_1}{G_2} = D'{G_2}\)

Phương pháp:

Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q) 

Lời giải:

a) Ta có: AD // B’C’, AD = B’C’ nên ADC’B’ là hình bình hành

Suy ra AB’ // DC’ nên AB‘ // (A’C’D) (1)

Ta có: (ACC’A‘) là hình bình hành nên AC // A’C‘

Suy ra AC // (A’C’D‘) (2)

Mà AB‘, AC thuộc (ACB‘) (3)

Từ (1), (2), (3) suy ra  (ACB‘) // (A‘C’D)

b) Gọi O, O’ lần lượt là tâm hình bình hành ABCD, A’B’C’D’

Trong (BDD’B’): B’O cắt BD’

Mà B’O thuộc (ACB’), BD’ cắt (ACB’) tại\({G_1}\)

Suy ra: B’O cắt BD’ tại\({G_1}\)

Tương tự, ta có: DO’ cắt BD’ tại\({G_2}\)

Ta có: tam giác \({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\) (do BD // B’D’)

Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)

Nên \(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{2}{3}\)

Do đó:\({G_1}\) là trọng tâm tam giác ACB’

Chứng minh tương tự ta có:\({G_2}\) là trọng tâm tam giác A’C’D

c) Ta có tam giác\({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\)

Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)

Nên \({G_1}B = \frac{1}{3}BD'(1)\)

Tương tự ta có:\(\frac{{{G_2}D'}}{{{G_2}B}} = \frac{{OD'}}{{DB}} = \frac{1}{2}\)

Nên \({G_2}D' = \frac{1}{3}{\rm{DD}}'(2)\)

Từ (1) và (2) suy ra\({G_1}B = {G_1}{G_2} = {G_2}D'\)

Bài 2 trang 113 SGK Toán 11 tập 1 - Cánh Diều

Cho hình hộp ABCD.A’B’C’D‘. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘. Chứng minh rằng:

a) NQ // A’D‘ và \(NQ = \frac{1}{2}A'D'\)

b) Tứ giác MNQC là hình bình hành

c) MN // (ACD‘)

d) (MNP) // (ACD‘)

Phương pháp:

- Hình tứ giác có các cặp cạnh song song là hình bình hành

- Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P)

- Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q) 

Lời giải:

a)

b)

c)

Do MNQC hình bình hành nên MN // QC

Mà QC ⊂ (ACD’) nên MN // (ACD’).

d)

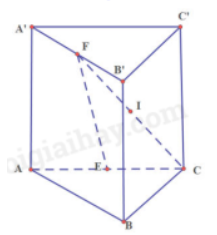
Bài 3 trang 113 SGK Toán 11 tập 1 - Cánh Diều

Cho hình lăng trụ tam giác ABC.A’B’C‘. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B‘.

a) Chứng minh rằng EF // (BCC’B’)

b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF.

Phương pháp:

Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P) 

Lời giải:

a) Gọi H là trung điểm của BC

Tam giác ABC có: E là trung điểm của AC

Suy ra EH // AB

Mà AB // A’B’

Do đó EH // A’B’ hay EH // B’F (1)

Ta có: EH // AB nên

Mà AB = A’B“,

Nên EH = B’F (2)

Từ (1) và (2) suy ra: EHB’F là hình bình hành

Suy ra EF // B’H

Suy ra EF // (BCC’B’)

b) Gọi K là trung điểm AB

Dễ dàng chứng minh FKBB’ là hình bình hành

Ta có: FK // BB‘

Mà BB‘ // CC‘

Suy ra FK // CC‘ (1)

Ta có: FK = BB‘, mà BB‘ = CC‘

Do đó: FK = CC‘ (2)

Từ (1) và (2) suy ra FKCC’ là hình bình hành

Suy ra C’K cắt CF tại trung điểm mỗi đường

Suy ra I là trung điểm của CF

Sachbaitap.com