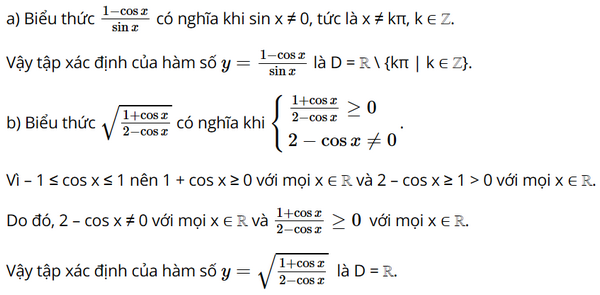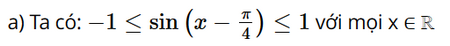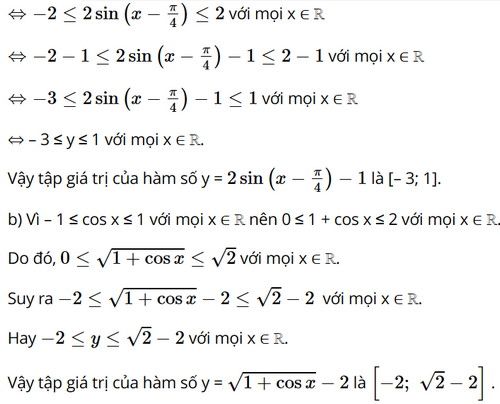Giải SGK Toán 11 trang 30 Kết Nối Tri Thức tập 1

Bài 1.15 trang 30 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Tìm tập xác định của các hàm số sau:

a) \(y = \frac{{1 - \cos x}}{{\sin x}}\);                                     

b) \(y = \sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} .\)

Phương pháp:

Hàm số xác định khi  biểu thức trong căn lớn hơn hoặc bằng 0

Lời giải:

Bài 1.16 trang 30 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Xét tính chẵn lẻ của các hàm số sau:

a) \(y = \sin 2x + \tan 2x\);                    b) \(y = \cos x + {\sin ^2}x\);

c) \(y = \sin x\cos 2x\);                          d) \(y = \sin x + \cos x\).

Phương pháp:

Sử dụng định nghĩa về hàm số chẵn, lẻ

Lời giải:

b) Tập xác định của hàm số y = f(x) = cos x + sin² x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = cos (– x) + sin² (– x) = cos x + (– sin x)² = cos x + sin² x = f(x), ∀ x ∈ D.

Vậy y = cos x + sin² x là hàm số chẵn.

c) Tập xác định của hàm số y = f(x) = sin x cos 2x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– x) . cos (– 2x) = – sin x . cos 2x = – f(x), ∀ x ∈ D.

Vậy y = sin x cos 2x là hàm số lẻ.

d) Tập xác định của hàm số y = f(x) = sin x + cos x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– x) + cos (– x) = – sin x + cos x ≠ – f(x).

Vậy y = sin x + cos x là hàm số không chẵn, không lẻ.

Bài 1.17 trang 30 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Tìm tập giá trị của các hàm số sau:

a) \(y = 2\sin \left( {x - \frac{\pi }{4}} \right) - 1\);                   

b) \(y = \sqrt {1 + \cos x}  - 2\);

Phương pháp:

Tập giá trị của hàm số là tập min – max của hàm số trên tập xác định

Lời giải:

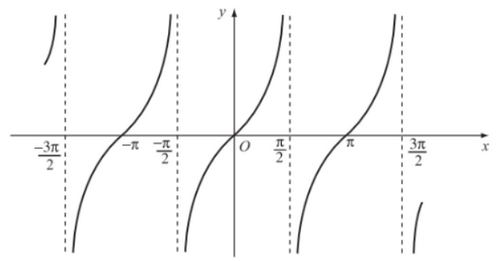
Bài 1.18 trang 30 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Từ đồ thị của hàm số \(y = \tan x\), hãy tìm các giá trị x sao cho \(\tan x = 0.\)

Phương pháp:

Quan sát đồ thị \(y = \tan x\) ta thấy hàm số tuần hoàn với chu kỳ \(\pi \)

Lời giải:

Ta có đồ thị của hàm số y = tan x như hình vẽ dưới đây.

Ta có tan x = 0 khi hàm số y = tan x nhận giá trị bằng 0 ứng với các điểm x mà đồ thị giao với trục hoành. Từ đồ thị ở hình trên ta suy ra y = 0 hay tan x = 0 khi x = kπ, k ∈ ℤ. 

Bài 1.19 trang 30 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Giả sử khi một cơn sóng biến đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số \(h\left( t \right) = 90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó h(t) là độ cao tính bằng centimet trên mực nước biển trung bình tại thời điểm t giây.

a) Tìm chu kì của sóng.

b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.

Phương pháp:

Sử dụng công thức chu kỳ sóng, chiều cao của sóng

Lời giải:

a) Chu kỳ của sóng \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\;\left( s \right)\)

b) Vì \( - 1 \le \cos \left( {\frac{\pi }{{10}}t} \right) \le 1\;\;\;\;\; \Rightarrow  - 90 \le 90\cos \left( {\frac{\pi }{{10}}t} \right) \le 90\)

Vậy chiều cao của sóng theo phương thẳng đứng là: \(90 + 90 = 180\;\left( {cm} \right)\)

Sachbaitap.com