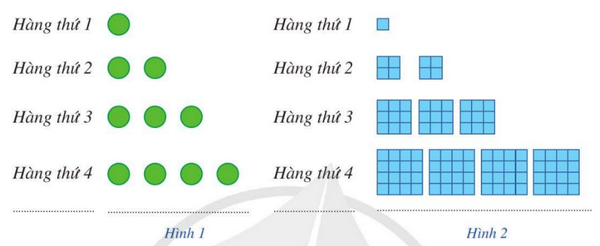
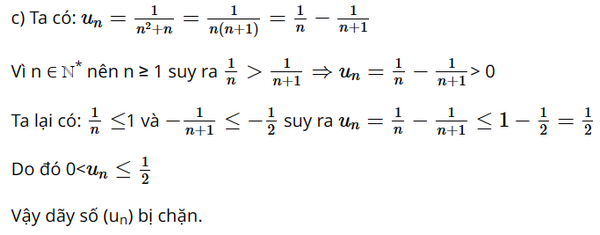Giải SGK Toán 11 trang 47, 48 Cánh Diều tập 1

Bài 1 trang 47 SGK Toán 11 tập 1 - Cánh Diều

Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát \({u_n}\) cho bởi công thức sau:

a)    \({u_n} = 2{n^2} + 1\)

b)    \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{2n - 1}}\)

c)    \({u_n} = \frac{{{2^n}}}{n}\)

d)    \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\)

Phương pháp:

Dựa vào kiến thức đã học để xác định 5 số hạng đầu của từng dãy số

Lời giải:

a)    Năm số hạng đầu của dãy số là: 3; 9; 19; 33; 51

b)    Năm số hạng đầu của dãy số là: \( - 1;\frac{1}{3}; - \frac{1}{5};\frac{1}{7}; - \frac{1}{9}\)

c)    Năm số hạng đầu của dãy số là: \(2;2;\frac{8}{3};4;\frac{{32}}{5}\)

d)    Năm số hạng đầu của dãy số là: \(2;\frac{9}{4};\frac{{64}}{{27}};\frac{{625}}{{256}};\frac{{7776}}{{3125}}\)

Bài 2 trang 47 SGK Toán 11 tập 1 - Cánh Diều

a)    Gọi \({u_n}\) là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức của số hạng tổng quát cho dãy số \(\left( {{u_n}} \right)\)

b)    Gọi \({v_n}\) là tổng diện tích của các hình tô màu ở hành thứ n trong Hình 2 (Mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hàng tổng quát cho dãy số \(\left( {{v_n}} \right)\)

Phương pháp:

Dựa vào kiến thức đã học để xác định

Lời giải:

a) Số chấm ở hàng thứ nhất là: u₁ = 1;

Số chấm ở hàng thứ hai là: u₂ = 2;

Số chấm ở hàng thứ ba là: u₃ = 3;

Số chấm ở hàng thứ tư là: u₄ = 4;

Vậy số chấm ở hàng thứ n là: u_n = n.

b) Diện tích của các ô màu ở hàng thứ nhất là: v₁ = 1 = 1³;

Diện tích của các ô màu ở hàng thứ hai là: v₂ = 8 = 2³;

Diện tích của các ô màu ở hàng thứ ba là: v₃ = 27 = 3³;

Diện tích của các ô màu ở hàng thứ tư là: v₄ = 64 = 4³;

Vậy diện tích của các ô màu ở hàng thứ n là: v_n = n³.

Bài 3 trang 48 SGK Toán 11 tập 1 - Cánh Diều

Xét tính tăng, giảm của mỗi dãy số \(\left( {{u_n}} \right)\), biết:

a)    \({u_n} = \frac{{n - 3}}{{n + 2}}\)

b)    \({u_n} = \frac{{{3^n}}}{{{2^n}.n!}}\)

c)    \({u_n} = {\left( { - 1} \right)^n}\left( {{2^n} + 1} \right)\)

Phương pháp:

Dựa vào định nghĩa tính tăng, giảm của dãy số để xác định

Lời giải:

a)    Xét:

  \(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{n + 1 - 3}}{{n + 1 + 2}} - \frac{{n - 3}}{{n + 2}}\\ = \frac{{n - 2}}{{n + 3}} - \frac{{n - 3}}{{n + 2}} = \frac{{{n^2} - 4 - {n^2} + 9}}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\\ = \frac{5}{{\left( {n + 3} \right)\left( {n + 2} \right)}} > 0\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)  

=> Dãy số là dãy số tăng

b)    Xét:

\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{{3^{n + 1}}}}{{{2^{n + 1}}.\left( {n + 1} \right)!}} - \frac{{{3^n}}}{{{2^n}.n!}}\\ = \frac{{{3^{n + 1}}}}{{{{2.2}^n}.n!.\left( {n + 1} \right)}} - \frac{{{3^n}}}{{{2^n}.n!}}\\ = \frac{{{3^{n + 1}}}}{{{2^{n + 1}}.\left( {n + 1} \right)!}} - \frac{{{3^n}.2\left( {n + 1} \right)}}{{{2^{n + 1}}.\left( {n + 1} \right)!}}\\ = \frac{{{3^n}\left( {3 - 2n - 2} \right)}}{{{2^{n + 1}}.\left( {n + 1} \right)!}} = \frac{{{3^n}\left( { - 2n + 1} \right)}}{{{2^{n + 1}}.\left( {n + 1} \right)!}} < 0\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)

 => Dãy số là dãy số giảm

c)    Xét:

\(\begin{array}{l}{u_{n + 1}} - {u_n} = {\left( { - 1} \right)^{n + 1}}.\left( {{2^{n + 1}} + 1} \right) - {\left( { - 1} \right)^n}.\left( {{2^n} + 1} \right)\\ = {\left( { - 1} \right)^n}\left[ {\left( { - 1} \right).\left( {{2^{n + 1}} + 1} \right) - {2^n} - 1} \right]\\ = {\left( { - 1} \right)^n}\left( { - {2^{n + 1}} - 1 - {2^n} - 1} \right)\\ = {\left( { - 1} \right)^n}\left( { - {{3.2}^n} - 2} \right)\end{array}\)

=> Dãy số không tăng không giảm

Bài 4 trang 48 SGK Toán 11 tập 1 - Cánh Diều

Trong các dãy số \(\left( {{u_n}} \right)\) được xác định như sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn?

a)    \({u_n} = {n^2} + 2\)

b)    \({u_n} =  - 2n + 1\)

c)    \({u_n} = \frac{1}{{{n^2} + n}}\)

Phương pháp:

Dựa vào kiến thức đã học để xác định

Lời giải:

a) Ta có: n ∈ ℕ^* nên n ≥ 1 suy ra n² + 2 ≥ 3

Do đó u_n ≥ 3

Vậy dãy số (u_n) bị chặn dưới bởi 3.

b) Ta có: n ∈ ℕ^* nên n ≥ 1 suy ra u_n = – 2n + 1 ≤ – 1

Do đó u_n ≤ – 1.

Vậy dãy số (u_n) bị chặn trên bởi – 1.

Bài 5 trang 48 SGK Toán 11 tập 1 - Cánh Diều

Cho dãy số dương \(\left( {{u_n}} \right)\). Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) là dãy số tăng khi và chỉ khi \(\frac{{{u_{n + 1}}}}{{{u_n}}} > 1\) với mọi \(n \in {\mathbb{N}^*}\).

Phương pháp:

Dựa vào kiến thức đã học để chứng minh

Lời giải:

Ta có:

\(\begin{array}{l}\frac{{{u_{n + 1}}}}{{{u_n}}} > 1\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow {u_{n + 1}} > {u_n}\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)

=> Luôn đúng

Bài 6 trang 48 SGK Toán 11 tập 1 - Cánh Diều

Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau: Lần đầu chị gửi 100 triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là 0,5% một tháng. Gọi \({P_n}\) (triệu đồng) là số tiền chị có trong ngân hàng sau n tháng

a)    Tính số tiền chị có trong ngân hàng sau 1 tháng

b)    Tính số tiền chị có trong ngân hàng sau 3 tháng

c)    Dự đoán công thức của \({P_n}\) tính theo n

Phương pháp:

Dựa vào kiến thức vừa học về dãy số để xác định.

Lời giải:

a) Số tiền chị có trong ngân hàng sau 1 tháng là:

P₁ = 100 + 100.0,5% + 6 = 100,5 + 6 (triệu đồng).

b) Số tiền chị có trong ngân hàng sau 2 tháng là:

P₂ = 100,5 + 6 + (100,5 + 6).0,5% + 6= (100,5 + 6)(1 + 0,5%) + 6 = 100,5(1 + 0,5%) + 6.(1 + 0,5%) + 6 (triệu đồng)

Số tiền chị có trong ngân hàng sau 3 tháng là:

P₃ = (100,5 + 6)(1 + 0,5%) + 6 + [(100,5 + 6)(1 + 0,5%) + 6 ].0,5% + 6

= 100,5.(1 + 0,5%)² + 6(1 + 0,5%)² + 6.(1 + 0,5%) + 6 (triệu đồng).

c) Số tiền chị có trong ngân hàng sau 4 tháng là:

P₄ = (100,5 + 6)(1 + 0,5%)² + 6.(1 + 0,5%) + 6 + [(100,5 + 6)(1 + 0,5%)² + 6.(1 + 0,5%) + 6]0,5% + 6

= 100,5.(1 + 0,5%)³ + 6.(1 + 0,5%)³ + 6(1 + 0,5%)² + 6.(1 + 0,5%) + 6

Số tiền chị có trong ngân hàng sau n tháng là:

P_n = 100,5.(1 + 0,5%)^n-1 + 6(1 + 0,5%)^n-1 + 6(1 + 0,5%)^n-2 + 6.(1 + 0,5%)^n-3 + ... + 6 với mọi n ∈ ℕ^*.

 Sachbaitap.com