Giải SGK Toán 11 trang 69, 70 Chân trời sáng tạo tập 1Giải bài 1, 2, 3 trang 69, bài 4, 5 trang 70 SGK Toán lớp 11 Chân trời sáng tạo tập 1. Tính tổng của các cấp số nhân lùi vô hạn sau. Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau: Bài 1 trang 69 SGK Toán 11 tập 1 - Chân trời sáng tạo Tìm các giới hạn sau: a) \(\lim \frac{{ - 2n + 1}}{n}\) b) \(\lim \frac{{\sqrt {16{n^2} - 2} }}{n}\) c) \(\lim \frac{4}{{2n + 1}}\) d) \(\lim \frac{{{n^2} - 2n + 3}}{{2{n^2}}}\) Phương pháp: Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu. Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng quy tắc tính giới hạn của thương để tính giới hạn. Lời giải: a) \(\lim \frac{{ - 2n + 1}}{n} = \lim \frac{{n\left( { - 2 + \frac{1}{n}} \right)}}{n} = \lim \left( { - 2 + \frac{1}{n}} \right) = - 2\) b) \(\lim \frac{{\sqrt {16{n^2} - 2} }}{n} = \lim \frac{{\sqrt {{n^2}\left( {16 - \frac{2}{{{n^2}}}} \right)} }}{n} = \lim \frac{{n\sqrt {16 - \frac{2}{{{n^2}}}} }}{n} = \lim \sqrt {16 - \frac{2}{{{n^2}}}} = 4\) c) \(\lim \frac{4}{{2n + 1}} = \lim \frac{4}{{n\left( {2 + \frac{1}{n}} \right)}} = \lim \left( {\frac{4}{n}.\frac{1}{{2 + \frac{1}{n}}}} \right) = \lim \frac{4}{n}.\lim \frac{1}{{2 + \frac{1}{n}}} = 0\) d) \(\lim \frac{{{n^2} - 2n + 3}}{{2{n^2}}} = \lim \frac{{{n^2}\left( {1 - \frac{2}{n} + \frac{3}{{{n^2}}}} \right)}}{{2{n^2}}} = \lim \frac{{1 - \frac{2}{n} + \frac{3}{{{n^2}}}}}{2} = \frac{1}{2}\) Bài 2 trang 69 SGK Toán 11 tập 1 - Chân trời sáng tạo Tính tổng của các cấp số nhân lùi vô hạn sau: a) \( - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + ... + {\left( { - \frac{1}{2}} \right)^n} + ...\) b) \(\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + ... + {\left( {\frac{1}{4}} \right)^n} + ...\) Phương pháp: Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) Lời giải:
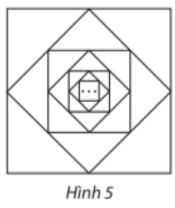
Bài 3 trang 69 SGK Toán 11 tập 1 - Chân trời sáng tạo Viết số thập phân vô hạn tuần hoàn \(0,444...\) dưới dạng một phân số. Phương pháp: Bước 1: Đưa số thập phân vô hạn tuần hoàn thành tổng của cấp số nhân lùi vô hạn. Bước 2: Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) Lời giải: \(0,444... = 0,4 + 0,04 + 0,004 + ...\) Số \(0,444...\) là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng \(0,4\) và công bội bằng \(\frac{1}{{10}}\). Do đó: \(0,444... = \frac{{0,4}}{{1 - \frac{1}{{10}}}} = \frac{4}{9}\) Bài 4 trang 70 SGK Toán 11 tập 1 - Chân trời sáng tạo Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5). a) Kí hiệu \({a_n}\) là diện tích của hình vuông thứ \(n\) và \({S_n}\) là tổng diện tích của \(n\) hình vuông đầu tiên. Viết công thức tính \({a_n},{S_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {S_n}\) (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông). b) Kí hiệu \({p_n}\) là chu vi của hình vuông thứ \(n\) và \({Q_n}\) là tổng chu vi của \(n\) hình vuông đầu tiên. Viết công thức tính \({p_n}\) và \({Q_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {Q_n}\) (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).
Phương pháp: Bước 1: Tìm cạnh của hình vuông thứ \(n\) dựa vào cạnh của hình vuông thứ \(n - 1\). Bước 2: Tính chu vi và diện tích của hình vuông thứ \(n\). Bước 3: Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) Lời giải:
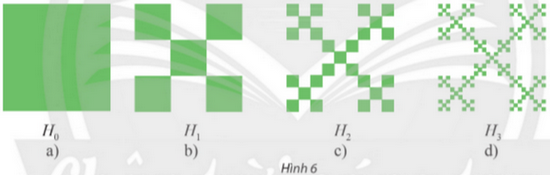
Bài 5 trang 70 SGK Toán 11 tập 1 - Chân trời sáng tạo Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau: Bắt đầu bằng một hình vuông \({H_0}\) cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông \({H_0}\) thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình \({H_1}\) (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của \({H_1}\) thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình \({H_2}\) (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình \({H_n}\left( {n = 1,2,3,...} \right)\).
Ta có: \({H_1}\) có 5 hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}\); \({H_2}\) có \(5.5 = {5^2}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}\);… Từ đó, nhận được hình \({H_n}\) có \({5^n}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{{{3^n}}}\). a) Tính diện tích \({S_n}\) của \({H_n}\) và tính \(\lim {S_n}\). b) Tính chu vi \({p_n}\) của \({H_n}\) và tính \(\lim {p_n}\). (Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích \(\lim {S_n}\) và chu vi \(\lim {p_n}\)). Phương pháp: Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) và công thức tính giới hạn cơ bản: \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\). Lời giải: a) \({S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,...\) \(\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0\) b) \({p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,...\) \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)\) Vì \(\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} = \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0\) và \(4.{\left( {\frac{5}{3}} \right)^n} > 0\) với mọi \(n\) nên \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty \). Sachbaitap.com
Xem thêm tại đây:
Bài 1. Giới hạn của dãy số
|
-

Giải SGK Toán 11 trang 79 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6 trang 79 SGK Toán lớp 11 Chân trời sáng tạo tập 1. Tìm các giới hạn sau. Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút.

 Tải ngay
Tải ngay