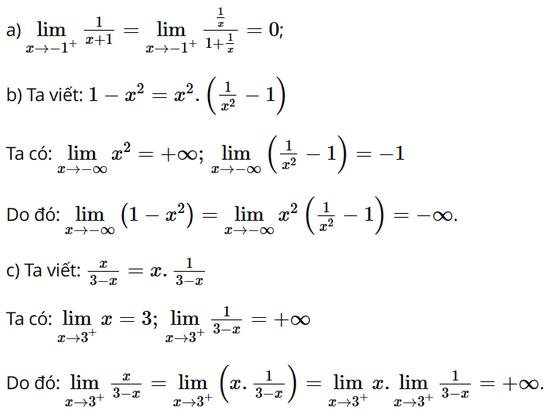Giải SGK Toán 11 trang 79 Chân trời sáng tạo tập 1

Bài 1 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - 2} \left( {{x^2} - 7x + 4} \right)\)  

b) \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{{x^2} - 9}}\)                                    

c) \(\mathop {\lim }\limits_{x \to 1} \frac{{3 - \sqrt {x + 8} }}{{x - 1}}\)

Phương pháp:

a) Áp dụng định lý giới hạn hữu hạn của hàm số.

b) Bước 1: Phân tích tử và mẫu thành tích các nhân tử.

Bước 2: Chia cả tử và mẫu cho nhân tử chung của tử và mẫu.

Bước 3: Áp dụng định lý giới hạn hữu hạn của hàm số.

c) Bước 1: Nhân cả tử và mẫu với liên hợp của tử.

Bước 2: Phân tích tử và mẫu thành tích các nhân tử.

Bước 3: Chia cả tử và mẫu cho nhân tử chung của tử và mẫu.

Bước 4: Áp dụng định lý giới hạn hữu hạn của hàm số.

Lời giải:

a) \(\mathop {\lim }\limits_{x \to  - 2} \left( {{x^2} - 7x + 4} \right) = \mathop {\lim }\limits_{x \to  - 2} \left( {{x^2}} \right) - \mathop {\lim }\limits_{x \to  - 2} \left( {7x} \right) + \mathop {\lim }\limits_{x \to  - 2} 4\)

                                                \( = \mathop {\lim }\limits_{x \to  - 2} \left( {{x^2}} \right) - 7\mathop {\lim }\limits_{x \to  - 2} x + \mathop {\lim }\limits_{x \to  - 2} 4 = {\left( { - 2} \right)^2} - 7.\left( { - 2} \right) + 4 = 22\)

b) \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{{x^2} - 9}} = \mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \mathop {\lim }\limits_{x \to 3} \frac{1}{{x + 3}} = \frac{{\mathop {\lim }\limits_{x \to 3} 1}}{{\mathop {\lim }\limits_{x \to 3} x + \mathop {\lim }\limits_{x \to 3} 3}} = \frac{1}{{3 + 3}} = \frac{1}{6}\)

c) \(\mathop {\lim }\limits_{x \to 1} \frac{{3 - \sqrt {x + 8} }}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {3 - \sqrt {x + 8} } \right)\left( {3 + \sqrt {x + 8} } \right)}}{{\left( {x - 1} \right)\left( {3 + \sqrt {x + 8} } \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{3^2} - \left( {x + 8} \right)}}{{\left( {x - 1} \right)\left( {3 + \sqrt {x + 8} } \right)}}\)

                                         \( = \mathop {\lim }\limits_{x \to 1} \frac{{1 - x}}{{\left( {x - 1} \right)\left( {3 + \sqrt {x + 8} } \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - \left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {3 + \sqrt {x + 8} } \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - 1}}{{3 + \sqrt {x + 8} }}\)

                                         \( = \frac{{\mathop {\lim }\limits_{x \to 1} \left( { - 1} \right)}}{{\mathop {\lim }\limits_{x \to 1} 3 + \mathop {\lim }\limits_{x \to 1} \sqrt {x + 8} }} = \frac{{ - 1}}{{3 + \sqrt {1 + 8} }} =  - \frac{1}{6}\)

Bài 2 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo

Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{ - {x^2}}&{khi\,\,x < 1}\\x&{khi\,\,x \ge 1}\end{array}} \right.\).

Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right);\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) (nếu có).

Phương pháp:

− Để tính giới hạn \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\), ta áp dụng định lý về giới hạn bên trái và giới hạn bên phải của hàm số.

− Để tính giới hạn \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\), ta so sánh hai giới hạn \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\).

                • Nếu \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right) = L\) thì \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = L\).

                • Nếu \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) thì không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).

Lời giải:

Bài 3 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{4x + 3}}{{2x}}\);      

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{2}{{3x + 1}}\);

c) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\).

Phương pháp:

Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.

Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.

Lời giải:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{4x + 3}}{{2x}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( {4 + \frac{3}{x}} \right)}}{{2x}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{4 + \frac{3}{x}}}{2} = \frac{{\mathop {\lim }\limits_{x \to  + \infty } 4 + \mathop {\lim }\limits_{x \to  + \infty } \frac{3}{x}}}{{\mathop {\lim }\limits_{x \to  + \infty } 2}} = \frac{{4 + 0}}{2} = 2\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{2}{{3x + 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{2}{{x\left( {3 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to  - \infty } \frac{2}{{3 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to  - \infty } 2}}{{\mathop {\lim }\limits_{x \to  - \infty } 3 + \mathop {\lim }\limits_{x \to  - \infty } \frac{1}{x}}} = 0.\frac{2}{{3 + 0}} = 0\).

c) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {{x^2}\left( {1 + \frac{1}{{{x^2}}}} \right)} }}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x\sqrt {1 + \frac{1}{{{x^2}}}} }}{{x\left( {1 + \frac{1}{x}} \right)}}\)

                                      \( = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = \frac{{\mathop {\lim }\limits_{x \to  + \infty } \sqrt {1 + \frac{1}{{{x^2}}}} }}{{\mathop {\lim }\limits_{x \to  + \infty } 1 + \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{x}}} = \frac{{\sqrt {1 + 0} }}{{1 + 0}} = 1\)

Bài 4 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - {1^ + }} \frac{1}{{x + 1}}\);              

b) \(\mathop {\lim }\limits_{x \to  - \infty } \left( {1 - {x^2}} \right)\);

c) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{x}{{3 - x}}\).

Phương pháp:

Bước 1: Đưa hàm số \(f\left( x \right)\) về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.

Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.

Lời giải:

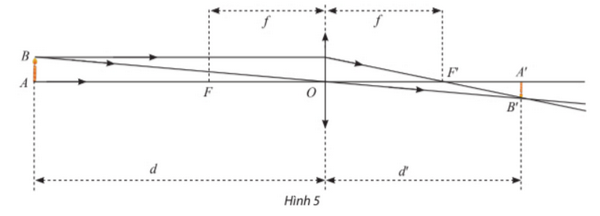
Bài 5 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo

Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút. 

a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau \(t\) phút kể từ khi bắt đầu bơm là \(C\left( t \right) = \frac{{30t}}{{400 + t}}\)(gam/lít).

b) Nồng độ muối trong hồ như thế nào nếu \(t \to  + \infty \).

Phương pháp:

a) Dựa vào dữ kiện của đề bài, biểu thị mối liên hệ giữa các đại lượng khối lượng muối, lượng nước trong hồ và nồng độ muối để viết biểu thức \(C\left( t \right)\).

b) Vận dụng phương pháp tính giới hạn của hàm số tại vô cực:

Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.

Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.

Lời giải:

a) Lượng nước biển bơm vào hồ sau \(t\) phút là: \(15t\) (lít).

Khối lượng muối có trong hồ sau \(t\) phút là: \(30.15t\) (gam).

Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(6000 + 15t\) (lít).

Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{30.15t}}{{6000 + 15t}} = \frac{{30.15t}}{{15\left( {400 + t} \right)}} = \frac{{30t}}{{400 + t}}\)(gam/lít).

b) \(\mathop {\lim }\limits_{t \to  + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to  + \infty } \frac{{30t}}{{400 + t}} = \mathop {\lim }\limits_{t \to  + \infty } \frac{{30t}}{{t\left( {\frac{{400}}{t} + 1} \right)}} = \mathop {\lim }\limits_{t \to  + \infty } \frac{{30}}{{\frac{{400}}{t} + 1}} = \frac{{30}}{{0 + 1}} = 30\) (gam/lít).

Vậy nồng độ muối trong hồ càng dần về 30 gam/lít, tức là nước trong hồ gần như là nước biển, khi \(t \to  + \infty \).

Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo

Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).

Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.

a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);        

b) \(\mathop {\lim }\limits_{d \to  + \infty } g\left( d \right)\).

Phương pháp:

a) Bước 1: Đưa hàm số \(f\left( x \right)\) về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.

Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.

b) Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.

Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.

Lời giải:

Sachbaitap.com