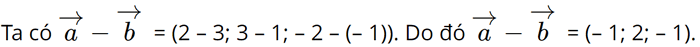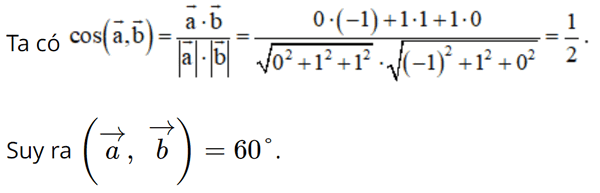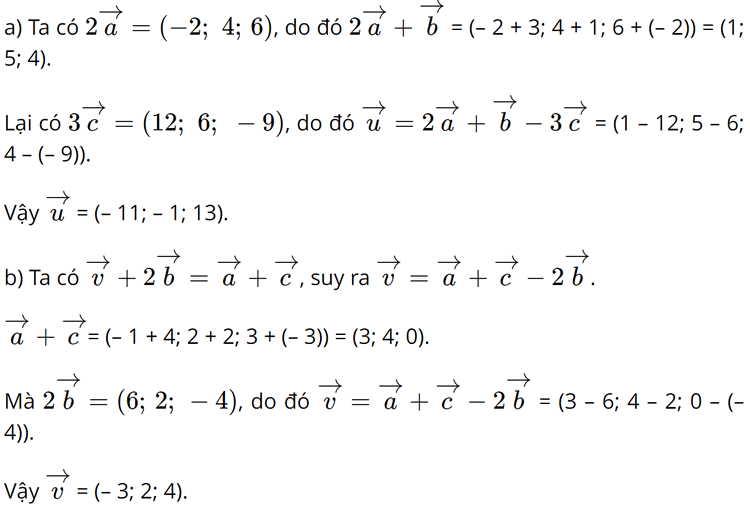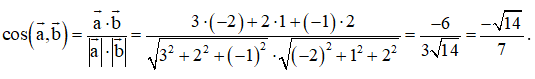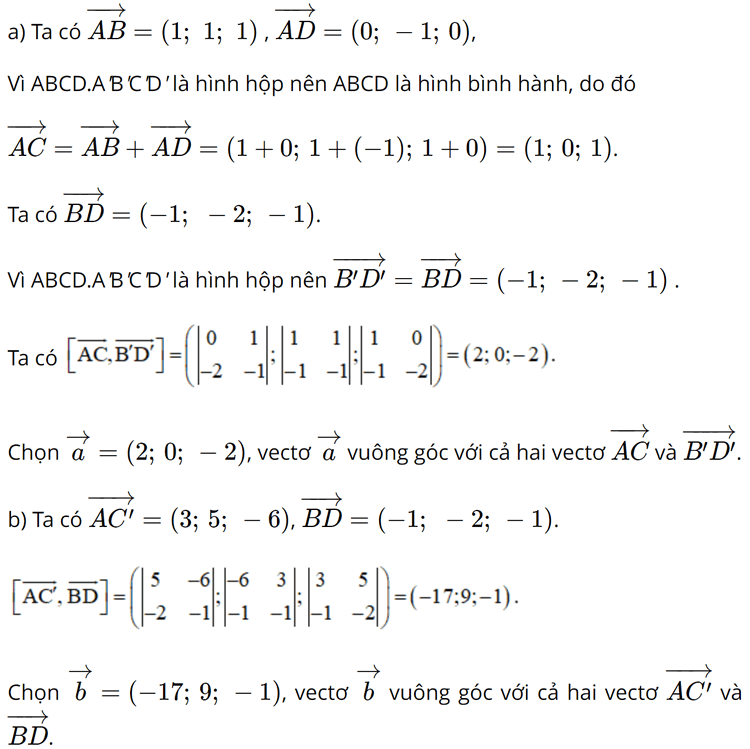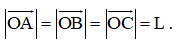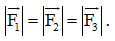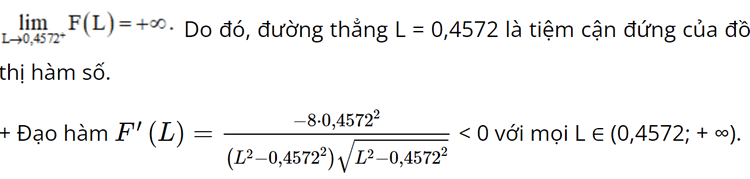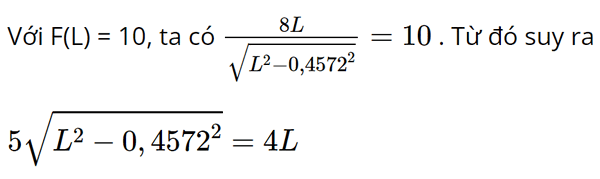Giải SGK Toán 12 tập 1 Cánh Diều trang 80, 81

Bài 1 trang 80 SGK Toán 12 Tập 1 Cánh Diều

Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a  = (2;3 - 2)\) và \(\overrightarrow b  = (3;1; - 1)\). Tọa độ của vecto \(\overrightarrow a  - \overrightarrow b \) là:

A. (1;-2;1)

B. (5;4;-3)

C. (-1;2;-1)

D. (-1;2;-3)

Phương pháp: 

Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a  - \overrightarrow b  = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)

Lời giải:

Đáp án đúng là: C

Bài 2 trang 80 SGK Toán 12 Tập 1 Cánh Diều

Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a  = (0;1;1)\) và \(\overrightarrow b  = ( - 1;1;0)\). Góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) bằng:

A. \(60^\circ \)

B. \(120^\circ \)

C. \(150^\circ \)

D. \(30^\circ \)

Phương pháp:

\(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

Lời giải:

Đáp án đúng là: A

Bài 3 trang 80 SGK Toán 12 Tập 1 Cánh Diều

Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a  = ( - 1;2;3)\), \(\overrightarrow b  = (3;1; - 2)\) và \(\overrightarrow c  = (4;2; - 3)\)

a) Tìm tọa độ của vecto \(\overrightarrow u  = 2\overrightarrow a  + \overrightarrow b  - 3\overrightarrow c \)

b) Tìm tọa độ của vecto \(\overrightarrow v \) sao cho \(\overrightarrow v  + 2\overrightarrow b  = \overrightarrow a  + \overrightarrow c \)

Phương pháp:

Áp dụng quy tắc cộng trừ hai vecto và nhân vecto với một số.

Lời giải:

Bài 4 trang 80 SGK Toán 12 Tập 1 Cánh Diều

Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a  = (2; - 2;1)\), \(\overrightarrow b  = (2;1;3)\). Hãy chỉ ra tọa độ của một vecto \(\overrightarrow c \) khác \(\overrightarrow 0 \) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)

Phương pháp:

Cho hai vecto \(\overrightarrow u  = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v  = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w  = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)

Lời giải:

Bài 5 trang 81 SGK Toán 12 Tập 1 Cánh Diều

Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a  = (3;2; - 1)\), \(\overrightarrow b  = ( - 2;1;2)\). Tính cosin của góc \((\overrightarrow a ,\overrightarrow b )\)

Phương pháp:

\(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

Lời giải:

Ta có 

Bài 6 trang 81 SGK Toán 12 Tập 1 Cánh Diều

Trong không gian với hệ tọa độ Oxyz, cho A(-2;3;0), B(4;0;5), C(0;2;-3).

a) Chứng minh rằng ba điểm A, B, C không thẳng hàng

b) Tính chu vi tam giác ABC

c) Tìm tọa độ trọng tâm G của tam giác ABC

d) Tính \(\cos \widehat {BAC}\)

Phương pháp:

a) A, B, C không thẳng hàng khi \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương

b) Chu vi tam giác ABC bằng tổng độ dài ba cạnh

c) Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC

d) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

Lời giải:

Bài 7 trang 81 SGK Toán 12 Tập 1 Cánh Diều

Cho hình hộp ABCD.A’B’C’D’, biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Hãy chỉ ra tọa độ của một vecto khác \(\overrightarrow 0 \) vuông góc với cả hai vecto trong mỗi trường hợp sau:

a) \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \)

b) \(\overrightarrow {AC'} \) và \(\overrightarrow {BD} \)

Phương pháp:

Cho hai vecto \(\overrightarrow u  = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v  = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w  = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)

Lời giải:

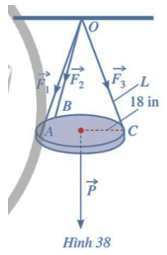
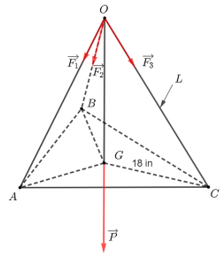
Bài 8 trang 81 SGK Toán 12 Tập 1 Cánh Diều

Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho tam giác ABC đều (Hình 38). Độ dài của ba đoạn dây OA, OB, OC đều bằng L. Trọng lượng của chiếc đèn là 24 N và bán kính của chiếc đèn là 18 in (1 inch 2.54 cm). Gọi F là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, F = F(L) là một hàm số với biến số là L 

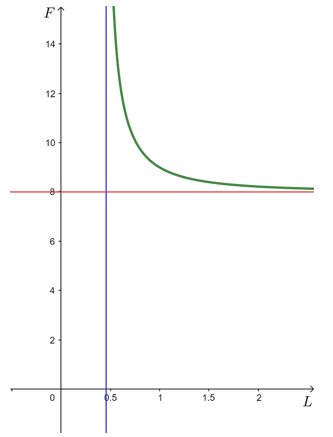
a) Xác định công thức tính hàm số F = F(L).

b) Khảo sát và vẽ đồ thị hàm số F = F(L).

c) Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 10 N.

Phương pháp:

a) Dùng phép chiếu để chiếu vecto lực lên phương phù hợp. Sau đó từ dữ kiện đề bài và các công thức phù hợp, ta xác định được hàm số

b) Tính đạo hàm, lập bảng biến thiên và vẽ đồ thị.

c) Từ hàm số thay các giá trị vào ta sẽ tìm được Lmin.

Lời giải:

a) Ta có 18 in = 45,72 cm = 0,4572 m.

Gọi G là trọng tâm tam giác ABC.

Vì tam giác ABC đều nên G là tâm đường tròn ngoại tiếp tam giác ABC.

Do đó, GA = GB = GC = 0,4572 m.

Theo bài ra ta có OA = OB = OC = L nên OG ⊥ (ABC) và 

Do đó, 

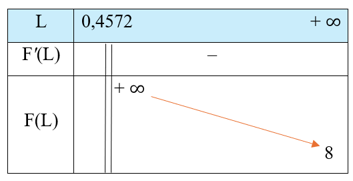
+ Bảng biến thiên:

Hàm số nghịch biến trên khoảng (0,4572; + ∞).

Hàm số không có cực trị.

+ Đồ thị hàm số được vẽ như hình dưới đây:

c) Ta có lực căng tối đa của mỗi sợi dây là 10 N.

⇔ 25L² – 5,255796 = 16L²

⇒ L = 0,762 ∈ (0,4572; + ∞).

Vậy chiều dài tối thiểu của mỗi sợi dây là L = 0,762 m = 76,2 cm = 30 in.

Sachbaitap.com