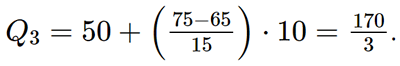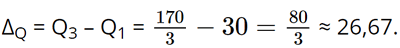Giải SGK Toán 12 tập 1 Cánh Diều trang 88Giải bài 1, 2, 3 trang 88 SGK Toán 12 Cánh Diều tập 1. Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày. Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của 1 công ty (đơn vị: triệu đồng). Bài 1 trang 88 SGK Toán 12 Tập 1 Cánh Diều Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.
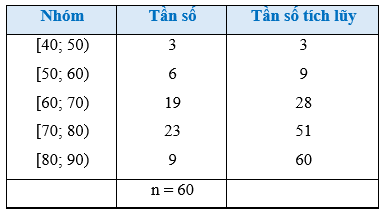
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: A. 50 B. 30 C. 6 D. 69,8 b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: A. 50 B. 40 C. 14,23 D. 70,87 Phương pháp: a) Khoảng biến thiên là hiệu của đầu mút phải nhóm cuối cùng và đầu mút trái nhóm đầu tiên b) Khoảng tứ phân vị là \({Q_3} - {Q_1}\) Lời giải: a) Đáp án đúng là: A Trong mẫu số liệu ghép nhóm ở Bảng 8, ta có: đầu mút trái của nhóm 1 là a1 = 40, đầu mút phải của nhóm 5 là a6 = 90. Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là: R = a6 – a1 = 90 – 40 = 50 (nghìn đồng). b) Đáp án đúng là: C Từ Bảng 8 ta có bảng sau:
Số phần tử của mẫu là n = 60. - Ta có: mà 9 < 15 < 28. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 3 là nhóm [60; 70) có s = 60; h = 10; n3 = 19 và nhóm 2 là nhóm [50; 60) có cf2 = 9. Áp dụng công thức, ta có tứ phân vị thứ nhất là
- Ta có: mà 28 < 45 < 51. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [70; 80) có t = 70; l = 10; n4 = 23 và nhóm 3 là nhóm [60; 70) có cf3 = 28. Áp dụng công thức, ta có tứ phân vị thứ ba là
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
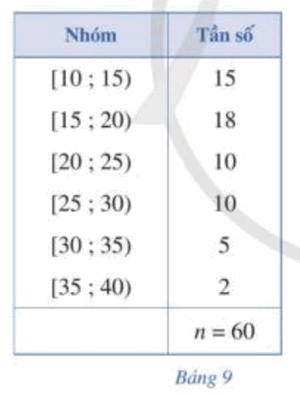
Bài 2 trang 88 SGK Toán 12 Tập 1 Cánh Diều Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của 1 công ty (đơn vị: triệu đồng)
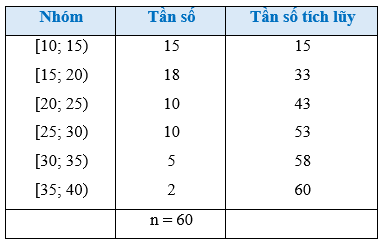
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó Phương pháp: a) Khoảng biến thiên là hiệu của đầu mút phải nhóm cuối cùng và đầu mút trái nhóm đầu tiên b) Khoảng tứ phân vị là \({Q_3} - {Q_1}\) Lời giải: a) Trong mẫu số liệu ghép nhóm ở Bảng 9, ta có: đầu mút trái của nhóm 1 là a1 = 10, đầu mút phải của nhóm 6 là a7 = 40. Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là: R = a7 – a1 = 40 – 10 = 30 (triệu đồng). b) Từ Bảng 9 ta có bảng sau:
Số phần tử của mẫu là n = 60. - Ta có: Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 1 là nhóm [10; 15) có s = 10; h = 5; n1 = 15. Áp dụng công thức, ta có tứ phân vị thứ nhất là
- Ta có: Áp dụng công thức, ta có tứ phân vị thứ ba là
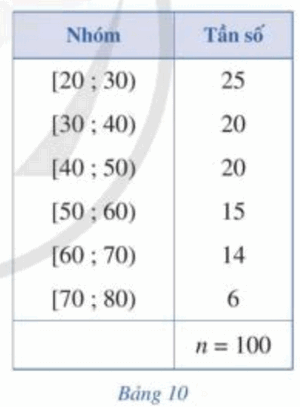
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là: ∆Q = Q3 – Q1 = 26 – 15 = 11 (triệu đồng). Bài 3 trang 88 SGK Toán 12 Tập 1 Cánh Diều Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
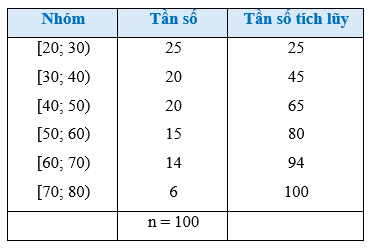
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó Phương pháp: a) Khoảng biến thiên là hiệu của đầu mút phải nhóm cuối cùng và đầu mút trái nhóm đầu tiên. b) Khoảng tứ phân vị là \({Q_3} - {Q_1}\). Lời giải: a) Trong mẫu số liệu ghép nhóm ở Bảng 10, ta có: đầu mút trái của nhóm 1 là a1 = 20, đầu mút phải của nhóm 6 là a7 = 80. Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là: R = a7 – a1 = 80 – 20 = 60. b) Từ Bảng 10 ta có bảng sau:
Số phần tử của mẫu là n = 100. - Ta có: Áp dụng công thức, ta có tứ phân vị thứ nhất là
- Ta có: Áp dụng công thức, ta có tứ phân vị thứ ba là
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
Sachbaitap.com
Xem thêm tại đây:
Bài 1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
|
-

Giải SGK Toán 12 tập 1 Cánh Diều trang 92
Giải bài 1, 2, 3 trang 92 SGK Toán 12 Cánh Diều tập 1. Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng 18.

 Tải ngay
Tải ngay
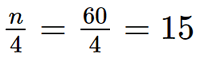
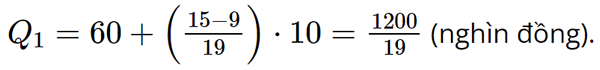
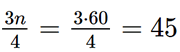
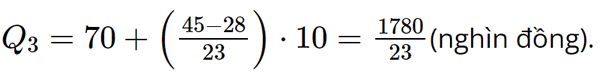
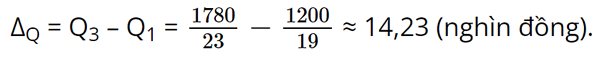
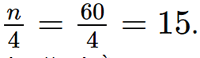
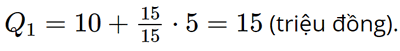
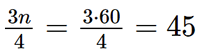 mà 43 < 45 < 53. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [25; 30) có t = 25; l = 5; n
mà 43 < 45 < 53. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [25; 30) có t = 25; l = 5; n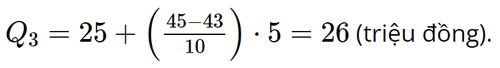
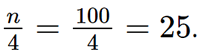 . Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25. Xét nhóm 1 là nhóm [20; 30) có s = 20; h = 10; n1 = 25.
. Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25. Xét nhóm 1 là nhóm [20; 30) có s = 20; h = 10; n1 = 25.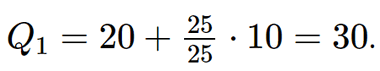
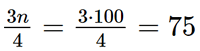 mà 65 < 75 < 80. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75. Xét nhóm 4 là nhóm [50; 60) có t = 50; l = 10; n4 = 15 và nhóm 3 là nhóm [40; 50) có cf3 = 65.
mà 65 < 75 < 80. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75. Xét nhóm 4 là nhóm [50; 60) có t = 50; l = 10; n4 = 15 và nhóm 3 là nhóm [40; 50) có cf3 = 65.