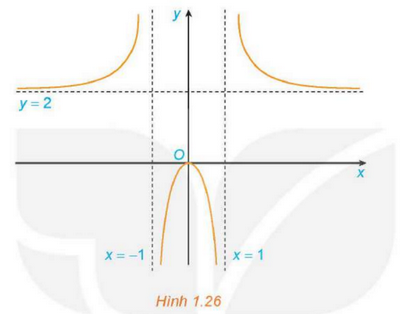
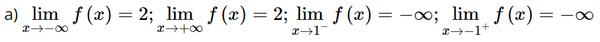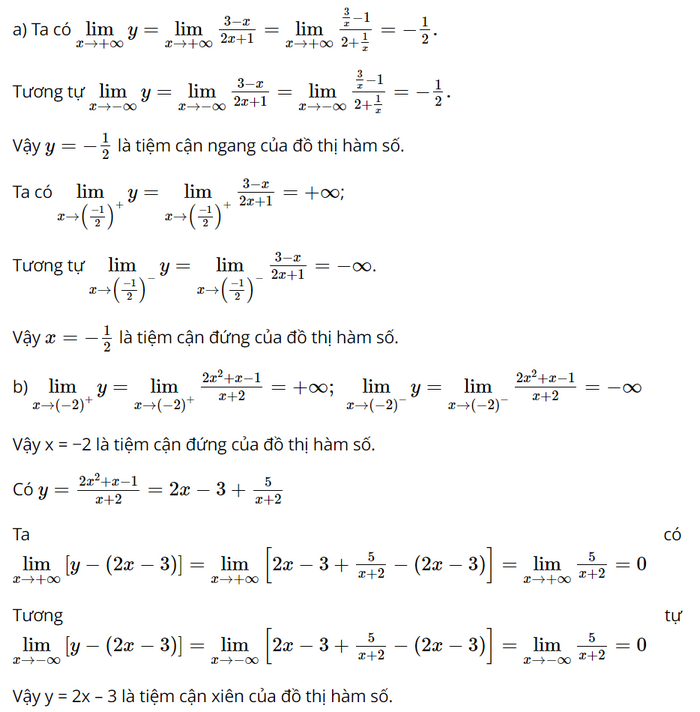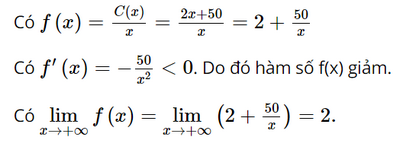Giải SGK Toán 12 tập 1 Kết nối tri thức trang 25Giải bài 1.16, 1.17, 1.18, 1.19, 1.20 trang 25 SGK Toán 12 Kết nối tri thức tập 1. Một mảnh vườn hình chữ nhật có diện tích bằng 144 m2 Biết độ dài một cạnh của mảnh vườn là x (m). a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn. b) Tìm các tiệm cận của đồ thị hàm số P(x). Bài 1.16 trang 25 SGK Toán 12 Tập 1 Kết nối tri thức Hình 1.26 là đồ thị của hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
Sử dụng đồ thị này, hãy: Phương pháp: Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \) Lời giải:
b) y = 2 là tiệm cận ngang của đồ thị hàm số x = 1 và x = −1 là các tiệm cận đứng của đồ thị hàm số. Bài 1.17 trang 25 SGK Toán 12 Tập 1 Kết nối tri thức Đường thẳng \(x = 1\) có phải là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\) không? Phương pháp: Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \) Lời giải:
Bài 1.18 trang 25 SGK Toán 12 Tập 1 Kết nối tri thức Tìm các tiệm cận của đồ thị hàm số sau: Phương pháp: Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \) Sử dụng kiến thức về khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\). Lời giải:
Bài 1.19 trang 25 SGK Toán 12 Tập 1 Kết nối tri thức Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là \(C\left( x \right) = 2x + 50\) (triệu đồng). Khi đó, \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Tính chất này nói lên điều gì? Phương pháp: Sử dụng kiến thức về giới hạn hàm số để tính. Lời giải:
Tính chất này nói lên rằng chi phí sản xuất trung bình cho mỗi sản phẩm sẽ giảm khi số lượng sản phẩm được sản xuất tăng lên và giới hạn của chi phí trung bình là 2 triệu đồng khi số lượng sản phẩm tiến gần đến vô cùng. Điều này có thể hiểu là khi sản xuất nhiều sản phẩm hơn, chi phí trung bình cho mỗi sản phẩm sẽ giảm và tiến gần đến một giá trị ổn định. Bài 1.20 trang 25 SGK Toán 12 Tập 1 Kết nối tri thức Một mảnh vườn hình chữ nhật có diện tích bằng \(144{m^2}\). Biết độ dài một cạnh của mảnh vườn là x (m). a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn. b) Tìm các tiệm cận của đồ thị hàm số P(x). Phương pháp: Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \) Sử dụng kiến thức về khái niệm đường tiệm cận xiên để tìm tiệm cận xiên: Đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\). Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài 3: Đường tiệm cận của đồ thị hàm số
|
-

Giải SGK Toán 12 tập 1 Kết nối tri thức trang 32
Giải bài 1.21, 1.22, 1.23, 1.24, 1.25 trang 32 SGK Toán 12 Kết nối tri thức tập 1. Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc.

 Tải ngay
Tải ngay