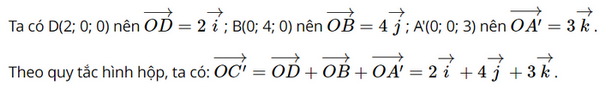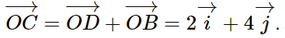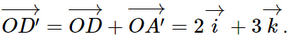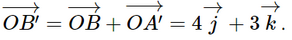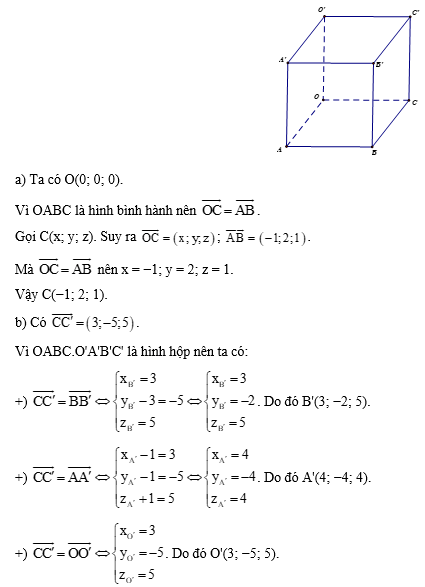Giải SGK Toán 12 tập 1 Kết nối tri thức trang 64, 65Giải bài 2.13, 2.14 trang 64, bài 2.15, 2.16, 2.17, 2.18, 2.19 trang 65 SGK Toán 12 Kết nối tri thức tập 1. Trong vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó. Bài 2.13 trang 64 SGK Toán 12 Tập 1 Kết nối tri thức Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \) đều khác \(\overrightarrow 0 \) và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng? a) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt song song với giá của các vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \). b) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lầnlượt trùng với giá của các vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \). c) Có thể lập được một hệ tọa độ Oxyz có các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt bằng các vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \). d) Có thể lập được một hệ tọa độ Oxyz có các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng phương các vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \). Phương pháp: Sử dụng kiến thức về hệ tọa độ trong không gian để tìm câu đúng: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz. Lời giải: Cả 4 đáp án trên đều đúng. Bài 2.14 trang 64 SGK Toán 12 Tập 1 Kết nối tri thức Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy) và mặt trần nhà trùng với mặt phẳng (Oxz).
Phương pháp: Sử dụng kiến thức về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz. Lời giải: Hình vẽ phù hợp là  Bài 2.15 trang 65 SGK Toán 12 Tập 1 Kết nối tri thức Trong không gian Oxyz, xác định tọa độ của vectơ \(\overrightarrow {AB} \) trong mỗi trườnghợp sau: a) \(A\left( {0;0;0} \right)\) và \(B\left( {4;2; - 5} \right)\); b) \(A\left( {1; - 3;7} \right)\) và \(B\left( {1; - 3;7} \right)\); c) \(A\left( {5;4;9} \right)\) và \(B\left( { - 5;7;2} \right)\). Phương pháp: Sử dụng kiến thức về thiết lập tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ vectơ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\). Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\). Lời giải:
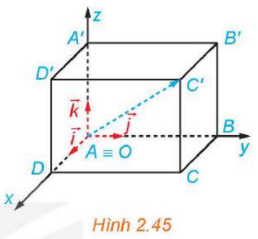
Bài 2.16 trang 65 SGK Toán 12 Tập 1 Kết nối tri thức Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau: a) A trùng với gốc tọa độ; b) A nằm trên tia Ox và \(OA = 2\); c) A nằm trên tia đối của tia Oy và \(OA = 3\). Phương pháp: Sử dụng kiến thức về tọa độ của điểm trong không gian để xác định tọa độ điểm A: Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết \(M = \left( {x;y;z} \right)\) hoặc \(M\left( {x;y;z} \right)\), trong đó x là hoành độ, y là tung độ, z là cao độ của M. Lời giải: a) A(0; 0; 0). b) A nằm trên tia Ox và OA = 2 nên c) A nằm trên tia đối của tia Oy và OA = 3 nên Bài 2.17 trang 65 SGK Toán 12 Tập 1 Kết nối tri thức Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Phương pháp: Sử dụng kiến thức về tọa độ của điểm trong không gian để xác định tọa độ các điểm: Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết \(M = \left( {x;y;z} \right)\) hoặc \(M\left( {x;y;z} \right)\), trong đó x là hoành độ, y là tung độ, z là cao độ của M. Lời giải: Đỉnh A trùng với gốc tọa độ nên A(0; 0; 0).
Do đó C'(2; 4; 3). Theo quy tắc hình bình hành, ta có: Do đó C(2; 4; 0). Theo quy tắc hình bình hành, ta có: Do đó D'(2; 0; 3). Theo quy tắc hình bình hành, ta có: Do đó B'(0; 4; 3). Bài 2.18 trang 65 SGK Toán 12 Tập 1 Kết nối tri thức Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {1;1; - 1} \right),B\left( {0;3;0} \right),C'\left( {2; - 3;6} \right)\). a) Xác định tọa độ của điểm C. b) Xác định các tọa độ đỉnh còn lại của hình hộp. Phương pháp: Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ vectơ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\). Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\). Lời giải:
Bài 2.19 trang 65 SGK Toán 12 Tập 1 Kết nối tri thức Trong vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó. Phương pháp: Sử dụng kiến thức về hệ tọa độ trong không gian để giải thích: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz. Lời giải: Khi máy bay di chuyển trên đường băng tức là máy bay di chuyển ở trên mặt đất,tức là thuộc mặt phẳng (Oxy). Do đó máy bay khi di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó. Sachbaitap.com
Xem thêm tại đây:
Bài 7: Hệ trục toạ độ trong không gian
|
-

Giải SGK Toán 12 tập 1 Kết nối tri thức trang 72
Giải bài 2.20, 2.21, 2.22, 2.23, 2.24 trang 72 SGK Toán 12 Kết nối tri thức tập 1. Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.

 Tải ngay
Tải ngay
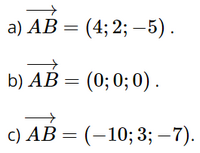
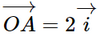 . Suy ra A(2; 0; 0).
. Suy ra A(2; 0; 0).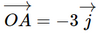 . Suy ra A(0; −3; 0).
. Suy ra A(0; −3; 0).