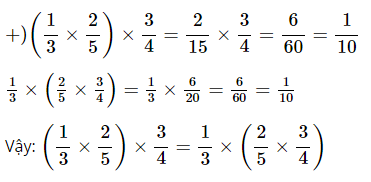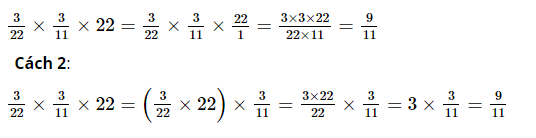Giải SGK Toán 4 trang 134 Luyện tập (tiếp)

Bài 1 trang 134 SGK Toán 4 tập 2

Câu hỏi:

a) Viết tiếp vào chỗ chấm: 

+) Nhận xét:   \( \displaystyle{2 \over 3} \times {4 \over 5} = \;...;\)                      \( \displaystyle{4 \over 5} \times {2 \over 3} =\; ...\)

Vậy: \( \displaystyle{2 \over 3} \times {4 \over 5} \cdots {4 \over 5} \times {2 \over 3}.\)

Tính chất giao hoán: Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi.

+) Nhận xét: \( \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} =  \cdots \)

                     \( \displaystyle{1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right) =  \cdots \)

Vậy: \( \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)\)

Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của phân số thứ hai và phân số thứ ba.

+) Nhận xét: \( \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} =  \cdots ;\)

                     \( \displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} =  \cdots \)

Vậy: \( \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}\)

Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân từng phân số của tổng với phân số thứ ba rồi cộng các kết quả lại. 

b) Tính bằng hai cách:

\( \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;\)                    \( \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};\)

\( \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}.\)

Lời giải:

a) \(+)\) \( \displaystyle \displaystyle{2 \over 3} \times {4 \over 5} = {{2 \times 4} \over {3 \times 5}} = {8 \over {15}}\)

          \( \displaystyle \displaystyle{4 \over 5} \times {2 \over 3} = {{4 \times 2} \over {5 \times 3}} = {8 \over {15}}\)

Vậy: \( \displaystyle \displaystyle{2 \over 3} \times {4 \over 5}= {4 \over 5} \times {2 \over 3}\)

Vậy: \( \displaystyle \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)\)

\(+)\) \( \displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {3 \over 5} \times {3 \over 4} = {{3 \times 3} \over {5 \times 4}} \) \( \displaystyle= {9 \over {20}}\)

\( \displaystyle \displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = {{1 \times 3} \over {5 \times 4}} + {{2 \times 3} \over {5 \times 4}} \)

\( \displaystyle \displaystyle= {3 \over {20}} + {6 \over {20}} \) \( \displaystyle \displaystyle= {{3 + 6} \over {20}} = {9 \over {20}}\)

Vậy: \( \displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}\)

b) 

1) \( \displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;\)

  Cách 1:

2) \( \displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};\)

  Cách 1: 

\( \displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} \) \( \displaystyle \displaystyle= \left( {{3 \over 6} + {2 \over 6}} \right) \times {2 \over 5} = {5 \over 6} \times {2 \over 5} \) \( \displaystyle \displaystyle= {2 \over 6} = {1 \over 3}\)

  Cách 2: 

\( \displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} = {1 \over 2} \times {2 \over 5} + {1 \over 3} \times {2 \over 5} \)\( \displaystyle = {1 \over 5} + {2 \over {15}} \) \( \displaystyle \displaystyle= {3 \over {15}} + {2 \over {15}} = {5 \over {15}} = {1 \over 3}\)

3) \( \displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}\)

  Cách 1:

\( \displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} \) \( \displaystyle = {{51} \over {105}} + {{34} \over {105}} \)\( \displaystyle \displaystyle= {{85} \over {105}}  = {{17} \over {21}}\)

   Cách 2:

\( \displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} = {{17} \over {21}} \times \left( {{3 \over 5} + {2 \over 5}} \right) \) \( \displaystyle \displaystyle= {{17} \over {21}} \times {5 \over 5} \) \( \displaystyle \displaystyle= {{17} \over {21}} \times 1 = {{17} \over {21}}\)

Bài 2 trang 134 SGK Toán 4 tập 2

Câu hỏi:

Tính chu vi hình chữ nhật có chiều dài \( \displaystyle{{4} \over {5}}m\) và chiều rộng \( \displaystyle \displaystyle{{2} \over {3}}m\).

Lời giải:

Chu vi hình chữ nhật là:

\( \displaystyle \left( {{4 \over 5} + {2 \over 3}} \right) \times 2 =  {{44} \over {15}}\;(m)\)

                     Đáp số: \( \displaystyle \displaystyle{{44} \over {15}}m\).

Bài 3 trang 134 SGK Toán 4 tập 2

Câu hỏi:

May một chiếc túi hết \( \displaystyle {{2} \over {3}}m\) vải. Hỏi may \(3\) chiếc túi như thế hết mấy mét vải ? 

Lời giải:

Tóm tắt:

Một chiếc túi: \( \displaystyle {{2} \over {3}}m\) vải

3 chiếc túi: ... mét vài?

Bài giải:

Số vải để may \(3\) cái túi là:

\( \displaystyle {2 \over 3} \times 3 = 2\;(m)\) 

                  Đáp số: \(2m\).

Sachbaitap.com