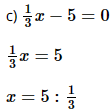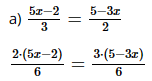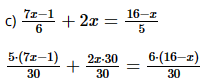Giải SGK Toán 8 Cánh Diều tập 2 trang 43, 44

a) 6x + 4 = 0

6x = ‒4

x = ‒4 : 6

b) ‒14x ‒ 28 = 0

‒14x = 28

x = 28 : (‒14)

x = ‒2.

Vậy phương trình có nghiệm x = ‒2.

x = 5 . 3

x = 15.

Vậy phương trình có nghiệm x = 15.

d) 3y ‒ 1 = ‒y + 19

3y + y = 19 + 1

4y = 20

y = 20 : 4

y = 5.

Vậy phương trình có nghiệm y = 5.

e) ‒2(z + 3) ‒ 5 = z + 4

‒2z ‒ 6 ‒ 5 = z + 4

‒2z ‒ z = 4 + 6 + 5

‒3z = 15

z = 15 : (‒3)

z = ‒5.

Vậy phương trình có nghiệm z = ‒5

 g) 3(t ‒ 10) = 7(t ‒ 10).

3t ‒ 30 = 7t ‒ 70

3t ‒ 7t = ‒ 70 + 30

‒4t = ‒ 40

t = ‒ 40 : (‒4)

t = 10

Vậy phương trình có nghiệm t = 10.

Bài 4 trang 44 SGK Toán 8 - Cánh Diều tập 2

Giải các phương trình:

a)      \(\frac{{5x - 2}}{3} = \frac{{5 - 3x}}{2}\);

b)     \(\frac{{10x + 3}}{{12}} = 1 + \frac{{6 + 8x}}{9}\);

c)      \(\frac{{7x - 1}}{6} + 2x = \frac{{16 - x}}{5}\).

Phương pháp:

Dựa vào quy tắc chuyển vế, quy tắc nhân và quy tắc phá ngoặc để giải phương trình.

Lời giải:

10x ‒ 4 = 15 ‒ 9x

10x + 9x = 15 + 4

19x = 19

x = 19 : 19

x = 1.

Vậy phương trình có nghiệm x = 1.

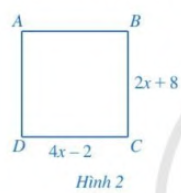
35x ‒ 5 + 60x = 96 ‒ 6x

35x + 60x + 6x = 96 + 5

101x = 101

x = 101 : 101

x = 1.

Vậy phương trình có nghiệm x = 1.

Bài 5 trang 44 SGK Toán 8 - Cánh Diều tập 2

Tìm \(x\), biết tứ giác \(ABCD\) là hình vuông (Hình 2).

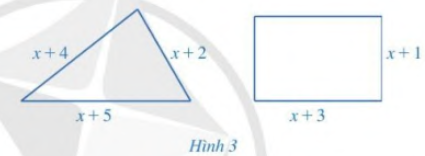
Phương pháp:

Dựa vào định nghĩa hình vuông có 4 cạnh bằng nhau để tìm \(x\).

Lời giải:

Do ABCD là hình vuông nên CD = BC hay 4x ‒ 2 = 2x + 8

Giải phương trình 4x ‒ 2 = 2x + 8 như sau:

4x ‒ 2 = 2x + 8

4x ‒ 2x = 8 + 2

2x = 10

x = 10 : 2

x = 5.

Vậy x = 5.

Bài 6 trang 44 SGK Toán 8 - Cánh Diều tập 2

Hình tam giác và hình chữ nhật ở Hình 3 có cùng chu vi. Viết phương trình biểu thị sự bằng nhau của chu vi hình tam giác, hình chữ nhật đó và tìm \(x\).

Phương pháp:

-         Viết biểu thức tính chu vi hình tam giác và biểu thức tính chu vi hình chữ nhật.

-         Viết phương trình thể hiện sự bằng nhau của chu vi hai hình.

Lời giải:

Chu vi hình tam giác là: x + 4 + x + 2 + x + 5 = 3x + 11.

Chu vi hình chữ nhật là: (x + 1 + x + 3) . 2 = (2x + 4) . 2 = 4x + 8

3x + 11 = 4x + 8.

Vậy phương trình biểu thị sự bằng nhau của chu vi hình tam giác, hình chữ nhật đó là 3x + 11 = 4x + 8.

Giải phương trình trên như sau:

3x + 11 = 4x + 8.

3x ‒ 4x = 8 ‒ 11

‒x = ‒3

x = 3

Vậy x = 3.

Bài 7 trang 44 SGK Toán 8 - Cánh Diều tập 2

Trong phòng thí nghiệm, chị Loan sử dụng cân Roberval để cân: bên đĩa thứ nhất đặt một quả cân nặng 500 g; bên đĩa thứ hai đặt hai vật cùng cân nặng \(x\) g và ba quả cân nhỏ, mỗi quả cân đó nặng 50 g. Chị Loan thấy cân thăng bằng. Viết phương trình biểu thị sự thăng bằng của cân khi đó.

Phương pháp:

-         Viết biểu thức biểu thị cân nặng ở mỗi đĩa.

-         Viết phương trình biểu thị sự thăng bằng của cân.

Lời giải:

Số cân nặng đặt bên đĩa thứ nhất là: 500 (g).

Số cân nặng đặt bên đĩa thứ hai là: 2x+3.50 = 2x + 150(g).

Phương trình ẩn x biểu thị sự thăng bằng của cân khi đó là:

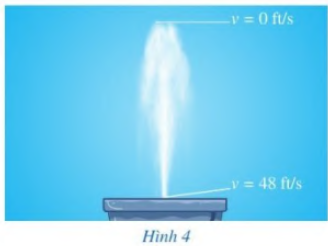
Bài 8 trang 44 SGK Toán 8 - Cánh Diều tập 2

Hình 4 mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1 ft = 0,3048 m). Tốc độ \(v\) (ft/s) của nước tại thời điểm \(t\) (s) được cho bởi công thức \(v = 48 - 32t\). Tìm thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa.

Phương pháp:

-         Tính \(t\) lúc giọt nước ở mặt đài phun nước.

-         Tính \(t\) lúc giọt nước đạt độ cao tối đa.

-         Tính thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa.

Lời giải:

Khi nước đạt đến độ cao tối đa thì v= 0 ft/s.

Suy ra tại thời điểm nước đạt đến độ cao tối đa ta có phương trình: 48−32t=0.

48−32t=0

‒32t = ‒ 48

t = ‒48 : (‒32)

t = 1,5

Vậy thời gian để nước đi từ mặt đài phun nước đến khi đạt được độ cao tối đa là 1,5 s.

Sachbaitap.com