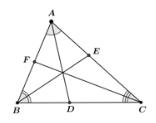
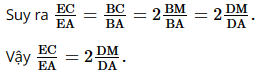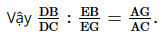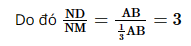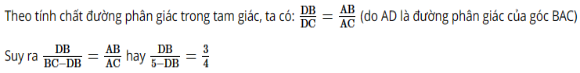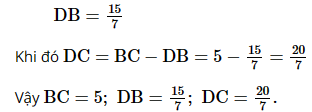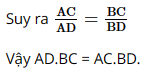Giải SGK Toán 8 Cánh Diều tập 2 trang 69

Bài 1 trang 69 SGK Toán 8 - Cánh Diều tập 2

Cho tam giác ABC có ba đường phân giácAD, BE, CF. Biết \(AB = 4,\,\,BC = 5,\,\,CA = 6\). Tính BD, CE, AF.

Phương pháp:

Dựa vào tính chất đường phân giác để tính độ dài các cạnh.

Lời giải:

Áp dụng tính chất đường phân giác cho tam giác ABC, ta có:

Do đó 6BD = 4(5 – BD)

          6BD = 20 – 4BD

          6BD + 4BD = 20

          10BD = 20

          BD = 2.

Do đó 4CE = 5(6 – CE)

          4CE = 30 – 5CE

          4CE + 5CE = 30

          9CE = 30

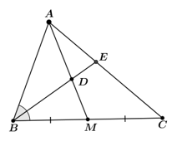
Bài 2 trang 69 SGK Toán 8 - Cánh Diều tập 2

Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\).

Phương pháp:

Dựa vào tính chất đường phân giác để chứng minh yêu cầu bài toán.

Lời giải:

Theo tính chất đường phân giác trong tam giác, ta có:

Mà BC = 2BM (do AM là đường trung tuyến của ∆ABC)

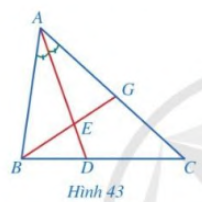
Bài 3 trang 69 SGK Toán 8 - Cánh Diều tập 2

Quan sát Hình 43 và chứng minh \(\frac{{DB}}{{DC}}:\frac{{EB}}{{EG}} = \frac{{AG}}{{AC}}\)

Phương pháp:

Sử dụng tính chất đường phân giác để chứng minh yêu cầu bài toán.

Lời giải:

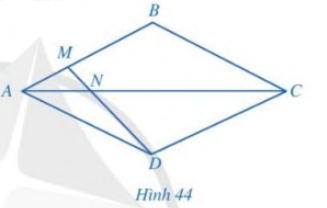
Theo tính chất đường phân giác trong tam giác, ta có:

Bài 4 trang 69 SGK Toán 8 - Cánh Diều tập 2

Cho hình thoi ABCD (Hình 4). Điểm M thuộc cạnh AB thỏa mãn \(AB = 3AM\). Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh \(ND = 3MN\).

Phương pháp:

Sử dụng tính chất đường phân giác để chứng minh yêu cầu bài toán.

Lời giải:

Do ABCD là hình thoi nên AD = AB và AC là đường phân giác của góc BAC.

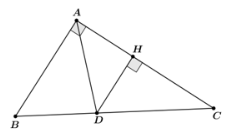
Vậy ND = 3MN.

Bài 5 trang 69 SGK Toán 8 - Cánh Diều tập 2

Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính: 

a) Độ dài các đoạn thẳng BC, DB, DC;

b) Khoảng cách từ điểm D đến đường thẳng AC;

c) Độ dài đường phân giác AD

Phương pháp:

Sử dụng định lý đường trung bình để tính độ dài các đoạn thẳng.

Lời giải:

a) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = 3² + 4² = 25 = 5²

Suy ra BC = 5.

Do đó 4DB = 3(5 – DB)

          4DB = 15 – 3DB

          4DB + 3DB = 15

          7DB = 15

b) Kẻ DH ⊥ AC (H ∈ AC).

Suy ra DH // AB (cùng vuông góc với AC)

Áp dụng hệ quả của định lí Thalès trong tam giác ABC với DH // AB, ta có:

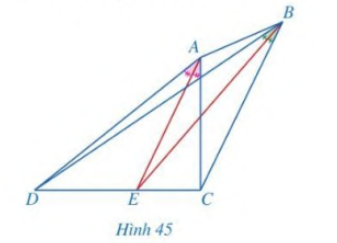
Bài 6 trang 69 SGK Toán 8 - Cánh Diều tập 2

Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45). Chứng minh \(AD.BC{\rm{ }} = {\rm{ }}AC.BD\).

Phương pháp:

Sử dụng định lý đường trung bình để chứng minh theo yêu cầu đề bài.

Lời giải:

Theo tính chất đường phân giác trong hai tam giác ACD và BCD, ta có:

Sachbaitap.com