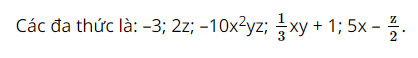Giải SGK Toán 8 trang 11 Chân trời sáng tạo tập 1

Bài 1 trang 11 SGK Toán 8 tập 1 - Chân trời sáng tạo

Chỉ ra các đơn thức, đa thức trong các biểu thức sau:

\( - 3\);             \(2z\); \(\dfrac{1}{3}xy + 1\);           \( - 10{x^2}yz\);          \(\dfrac{4}{{xy}}\);    \(5x - \dfrac{z}{2}\); \(1 + \dfrac{1}{y}\)

Phương pháp:

- Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến

- Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Lời giải:

Các đơn thức là: –3; 2z; –10x²yz.

Bài 2 trang 11 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.

\(5xyx\);          \( - xyz\dfrac{2}{3}y\);           \( - 2{x^2}\left( { - \dfrac{1}{6}} \right)x\) 

Phương pháp:

- Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.

- Số nói trên gọi là hệ số.

- Tổng số mũ của tất cả các biến có trong đơn thức (có hệ số khác \(0\)) gọi là bậc của đơn thức đó.

Lời giải:

Thu gọn các đơn thức:

• 5xyx = 5(x.x)y = 5x²y;

Bài 3 trang 11 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thu gọn và tìm bậc của mỗi đa thức sau:

a) \(M = x - 3 - 4y + 2x - y\) 

b) \(N =  - {x^2}t + 13{t^3} + x{t^2} + 5{t^3} - 4\)

Phương pháp:

Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng với nhau.

Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

Lời giải:

a) M = x – 3 – 4y + 2x – y

= (x + 2x) + (–4y – y) – 3

        = 3x – 5y – 3

Ba hạng tử của đa thức M có bậc lần lượt là 1; 1; 0. Do đó bậc của đa thức M bằng 1.

b) N = –x²t + 13t³ + xt² + 5t³ – 4.

        = –x²t + (13t³ + 5t³) + xt² – 4

        = –x²t + 18t³ + xt² – 4

Bài 4 trang 11 SGK Toán 8 tập 1 - Chân trời sáng tạo

Tính giá trị của đa thức \(P = 3x{y^2} - 6xy + 8xz + x{y^2} - 10xz\) tại \(x =  - 3\); \(y =  - \dfrac{1}{2}\); \(z = 3\).

Phương pháp:

- Thu gọn đa thức \(P\).

- Tính giá trị của đa thức thu gọn khi \(x =  - 3\); \(y =  - \dfrac{1}{2}\); \(z = 3\).

Lời giải:

Thu gọn đa thức P:

P = 3xy² – 6xy + 8xz + xy² – 10xz

   = (3xy² + xy²) – 6xy + (8xz – 10xz)

   = 4xy² – 6xy – 2xz.

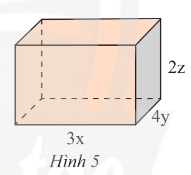
Bài 5 trang 11 SGK Toán 8 tập 1 - Chân trời sáng tạo

Viết biểu thức biểu thị thể tích \(V\) và diện tích xung quanh \(S\) của hình hộp chữ nhật trong Hình \(5\).

Tính giá trị của \(V\), \(S\) khi \(x = 4\)cm; \(y = 2\)cm và \(z = 1\)cm.

Phương pháp:

a) Công thức tính thể tích và diện tích xung quanh của hình hộp chữ nhật:

\(V = a.b.h\)

\(S = \left( {a + b} \right).2.h\)

Trong đó \(V\), \(S\), \(a\), \(b\), \(h\) lần lượt là thể tích, diện tích xung quanh, chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật.

b) Tính giá trị biểu thức \(V\), \(S\) khi \(x = 4\)cm; \(y = 2\)cm và \(z = 1\)cm.

Lời giải:

Biểu thức biểu thị thể tích V của hình hộp chữ nhật trong Hình 5 là:

V = 3x.4y.2z = 24xyz (đơn vị thể tích).

Biểu thức biểu thị diện tích xung quanh S của hình hộp chữ nhật trong Hình 5 là:

S = 2.(3x + 4y).2z = 4z(3x + 4y) (đơn vị diện tích).

Thay x = 4 cm, y = 2 cm và z = 1 cm vào biểu thức V, S ta được:

V = 24xyz = 24.4.2.1 = 192 (cm³).

S = 4.1.(3.4 + 4.2) = 4.(12 + 8) = 80 (cm²).

 Sachbaitap.com