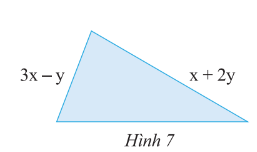
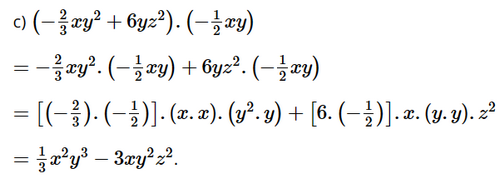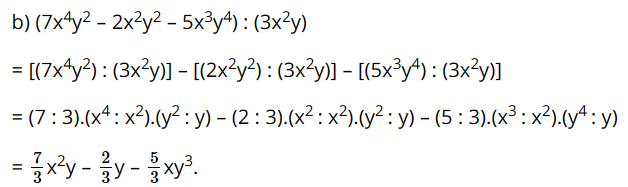Giải SGK Toán 8 trang 17 Chân trời sáng tạo tập 1Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 17 SGK Toán lớp 8 chân trời sáng tạo tập 1. Bài 2. Tìm độ dài cạnh còn thiếu của tam giác ở Hình 7, biết rằng tam giác có chu vi bằng 7x + 5y. Bài 1 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Tính: a) \(x + 2y + \left( {x - y} \right)\) b) \(2x - y - \left( {3x - 5y} \right)\) c) \(3{x^2} - 4{y^2} + 6xy + 7 + \left( { - {x^2} + {y^2} - 8xy + 9x + 1} \right)\) d) \(4{x^2}y - 2x{y^2} + 8 - \left( {3{x^2}y + 9x{y^2} - 12xy + 6} \right)\) Phương pháp: Áp dụng các quy tắc: - Dấu ngoặc - Tính chất giao hoán và kết hợp của phép cộng - Cộng, trừ đơn thức đồng dạng Lời giải: a) x + 2y + (x – y) = x + 2y + x – y = (x + x) + (2y – y) = 2x + y. b) 2x – y – (3x – 5y) = 2x – y – 3x + 5y = (2x – 3x) + (–y + 5y) = –x + 4y. c) 3x2 – 4y2 + 6xy + 7 + (–x2 + y2 – 8xy + 9x + 1) = 3x2 – 4y2 + 6xy + 7 – x2 + y2 – 8xy + 9x + 1 = (3x2 – x2) + (– 4y2 + y2) + (6xy – 8xy) + (7 + 1) + 9x = 2x2 – 3y2 – 2xy + 8 + 9x. d) 4x2y – 2xy2 + 8 – (3x2y + 9xy2 – 12xy + 6). = 4x2y – 2xy2 + 8 – 3x2y – 9xy2 + 12xy – 6 = (4x2y – 3x2y) + (– 2xy2 – 9xy2) + (8 – 6) + 12xy = x2y – 11xy2 + 2 + 12xy. Bài 2 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Tìm độ dài cạnh còn thiếu của tam giác ở Hình 7, biết rằng tam giác có chu vi bằng \(7x + 5y\).
Phương pháp: Áp dụng quy tắc trừ đa thức Lời giải: Độ dài cạnh còn thiếu của tam giác ở Hình 7 là: (7x + 5y) – (3x – y) – (x + 2y) = 7x + 5y – 3x + y – x – 2y = (7x – 3x – x) + (5y + y – 2y) = 3x + 4y. Vậy độ dài cạnh còn thiếu của tam giác ở Hình 7 là 3x + 4y. Bài 3 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Thực hiện các phép nhân: a) \(3x\left( {2xy - 5{x^2}y} \right)\) b) \(2{x^2}y\left( {xy - 4x{y^2} + 7y} \right)\) c) \(\left( { - \frac{2}{3}xy^2 + 6y{z^2}} \right).\left( { - \frac{1}{2}xy} \right)\) Phương pháp: Áp dụng quy tắc nhân đa thức với đơn thức, nhân đơn thức với đơn thức Lời giải: a) 3x(2xy – 5x2y) = 3x.2xy – 3x.5x2y = (3.2).(x.x).y – (3.5).(x.x2).y = 6x2y – 15x3y. b) 2x2y(xy – 4xy2 + 7y) = 2x2y.xy – 2x2y.4xy2 + 2x2y.7y = 2.(x2.x).(y.y) – (2.4).(x2.x).(y.y2) + (2.7).x2.(y.y) = 2x3y2 – 8x3y3 + 14x2y2.
Bài 4 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Thực hiện các phép nhân: a) \(\left( {x - y} \right)\left( {x - 5y} \right)\) b) \(\left( {2x + y} \right)\left( {4{x^2} - 2xy + {y^2}} \right)\) Phương pháp: Áp dụng quy tắc nhân đa thức với đa thức, nhân đơn thức với đơn thức. Lời giải: a) (x – y)(x – 5y) = x.(x – 5y) – y.(x – 5y) = x.x – x.5y – y.x + y.5y = x2 – 5xy – xy + 5y2 = x2 – 6xy + 5y2. b) (2x + y)(4x2 – 2xy + y2) = 2x.(4x2 – 2xy + y2) + y.(4x2 – 2xy + y2) = 2x.4x2 – 2x.2xy + 2x.y2 + y.4x2 – y.2xy + y.y2 = 8x3 – 4x2y + 2xy2 + 4x2y – 2xy2 + y3 = 8x3 + (– 4x2y + 4x2y) + (2xy2 – 2xy2) + y3 = 8x3 + y3. Bài 5 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Thực hiện các phép chia: a) \(20{x^3}{y^5}:\left( {5{x^2}{y^2}} \right)\) b) \(18{x^3}{y^5}:\left[ {3{{\left( { - x} \right)}^3}{y^2}} \right]\) Phương pháp: Áp dụng quy tắc chia đơn thức cho đơn thức. Lời giải: a) 20x3y5 : (5x2y2) = (20 : 5).(x3 : x2).(y5 : y2) = 4xy3. b) 18x3y5 : [3(–x)3y2] = 18x3y5 : [–3x3y2] = [18 : (–3)].(x3 : x3).(y5 : y2) = –6y3. Bài 6 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Thực hiện các phép chia: a) \(\left( {4{x^3}{y^2} - 8{x^2}y + 10xy} \right):\left( {2xy} \right)\) b) \(\left( {7{x^4}{y^2} - 2{x^2}{y^2} - 5{x^3}{y^4}} \right):\left( {3{x^2}y} \right)\) Phương pháp: Áp dụng quy tắc chia đa thức cho đơn thức, chia đơn thức cho đơn thức Lời giải: a) (4x3y2 – 8x2y + 10xy) : (2xy) = [(4x3y2) : (2xy)] – [(8x2y) : (2xy)] + [(10xy) : (2xy)] = (4 : 2).(x3 : x).(y2 : y) – (8 : 2).(x2 : x).(y : y) + (10 : 2).(x : x).(y : y) = 2x2y – 4x + 5. Bài 7 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Tính giá trị của biểu thức: a) \(3{x^2}y - \left( {3xy - 6{x^2}y} \right) + \left( {5xy - 9{x^2}y} \right)\) tại \(x = \frac{2}{3}\), \(y = - \frac{3}{4}\) b) \(x\left( {x - 2y} \right) - y\left( {{y^2} - 2x} \right)\) tại \(x = 5\), \(y = 3\) Phương pháp: - Thu gọn đa thức - Tính giá trị của đa thức thu gọn Lời giải: a) Thu gọn biểu thức: 3x2y – (3xy – 6x2y) + (5xy – 9x2y) = 3x2y – 3xy + 6x2y + 5xy – 9x2y = (3x2y + 6x2y – 9x2y) + (– 3xy + 5xy) = 2xy
b) Thu gọn biểu thức: x(x – 2y) – y(y2 – 2x) = x.x – x.2y – y.y2 + y.2x = x2 – 2xy – y3 + 2xy = x2 + (– 2xy + 2xy) – y3 = x2 – y3 Thay x = 5 và y = 3 vào biểu thức đã thu gọn ta có: 52 – 33 = 25 – 27 = –2. Bài 8 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo Trên một dòng sông, để đi được \(10\)km, một chiếc xuồng tiêu tốn \(a\) lít dầu khi xuôi dòng và tiêu tốn \(\left( {a + 2} \right)\) lít dầu khi ngược dòng. Viết biểu thức biểu thị số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A. Biết khoẳng cách giữa hai bến là \(b\) km. Phương pháp: Tính số lít dầu tiêu tốn khi đi 1 km xuôi dòng, 1 km ngược dòng rồi tính số lít tiêu tốn khi đi quãng sông đó. Lời giải:
Bài 9 trang 17 SGK Toán 8 tập 1 - Chân trời sáng tạo a) Tính chiều dài của hình chữ nhật có diện tích bằng \(6xy + 10{y^2}\) và chiều rộng bằng \(2y\). b) Tính diện tích đáy của hình hộp chữ nhật có thể tích bằng \(12{x^3} - 3x{y^2} + 9{x^2}y\) và chiều cao bằng \(3x\). Phương pháp: a) Áp dụng công thức tính chiều dài hình chữ nhật, quy tắc chia đa thức cho đơn thức b) Áp dụng công thức tính diện tích đáy của hình hộp chữ nhật, quy tắc chia đa thức cho đơn thức Lời giải: a) Chiều dài của hình chữ nhật đã cho là: (6xy + 10y2) : (2y) = [(6xy) : (2y)] + [(10y2) : (2y)] = (6 : 2).x.(y : y) + (10 : 2).(y2 : y) = 3x + 5y. Vậy chiều dài của hình chữ nhật đã cho là 3x + 5y. b) Diện tích đáy của hình hộp chữ nhật đã cho là: Sđáy = V : h = (12x3 – 3xy2 + 9x2y) : (3x) = [(12x3) : (3x)] – [(3xy2) : (3x)] + [(9x2y) : (3x)] = (12 : 3).(x3 : x) – (3 : 3).(x : x).y2 + (9 : 3).(x2 : x).y = 4x2 – y2 + 3xy. Vậy diện tích đáy của hình hộp chữ nhật đã cho là 4x2 – y2 + 3xy. Sachbaitap.com
Xem thêm tại đây:
Bài 2. Các phép toán với đa thức nhiều biến
|
-

Giải SGK Toán 8 trang 22 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 22 SGK Toán lớp 8 chân trời sáng tạo tập 1. Bài 1. Viết các biểu thức sau thành đa thức, bài 2. Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

 Tải ngay
Tải ngay