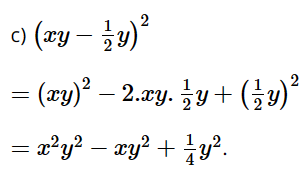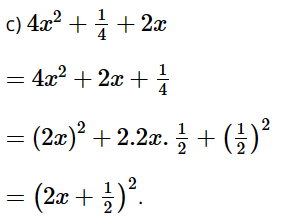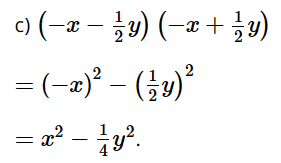Giải SGK Toán 8 trang 22 Chân trời sáng tạo tập 1

Bài 1 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Tính:

a) \({\left( {3x + 4} \right)^2}\)                                  b) \({\left( {5x - y} \right)^2}\)                                   c) \({\left( {xy - \dfrac{1}{2}y} \right)^2}\)

Phương pháp:

Áp dụng hằng đẳng thức: Bình phương của một tổng, một hiệu.

Lời giải:

a) (3x + 4)²

= (3x)² + 2.3x.4 + 4²

= 9x² + 24x + 16.

 b) (5x – y)²

= (5x)² – 2.5x.y + y²

= 25x² – 10xy + y².

Bài 2 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) \({x^2} + 2x + 1\)               b) \(9 - 24x + 16{x^2}\)                      c) \(4{x^2} + \dfrac{1}{4} + 2x\)

Phương pháp:

Biến đổi biểu thức về dạng vế phải của hằng đẳng thức: bình phương của một tổng, một hiệu rồi áp dụng

Lời giải:

a) x² + 2x + 1

= x² + 2.x.1 + 1²

= (x + 1)².

b) 9 – 24x + 16x²

= 3² – 2.3.4x + (4x)²

= (3 – 4x)².

Ta cũng có thể viết như sau:

9 – 24x + 16x²

= 16x² – 24x + 9

= (4x)² – 2.4x.3 + 3²

= (4x – 3)².

Bài 3 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Viết các biểu thức sau thành đa thức:

a) \(\left( {3x - 5} \right)\left( {3x + 5} \right)\)                                b) \(\left( {x - 2y} \right)\left( {x + 2y} \right)\)                       c) \(\left( { - x - \dfrac{1}{2}y} \right)\left( { - x + \dfrac{1}{2}y} \right)\)

Phương pháp:

Áp dụng hằng đẳng thức: Hiệu của hai bình phương

Lời giải:

a) (3x – 5)(3x + 5)

= (3x)² – 5²

= 9x² – 25.

b) (x – 2y)(x + 2y)

= x² – (2y)²

= x² – 4y².

Bài 4 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng \(2x + 3\) dưới dạng đa thức

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng \(3x - 2\) dưới dạng đa thức.

Phương pháp:

a) Áp dụng công thức tính diện tích hình vuông rồi áp dụng hằng đẳng thức Bình phương của một tổng

b) Áp dụng công thức tính thể tích khối lập phương rồi áp dụng hằng đẳng thức Lập phương của một hiệu

Lời giải:

a) Biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 là:

(2x + 3)² = (2x)² + 2.2x.3 + 3² = 4x² + 12x + 9.

b) Biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 là:

(3x – 2)³ = (3x)³ – 3.(3x)².2 + 3.3x.2² – 2³

               = 27x³ – 54x² + 36x – 8.

Bài 5 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Tính nhanh:

a) \(38.42\)                               b) \({102^2}\)                          c) \({198^2}\)              d) \({75^2} - {25^2}\)

Phương pháp:

a) Biến đổi thành tích của tổng và hiệu của hai số tự nhiên.

b) Biến đổi thành tổng của hai số tự nhiên trong đó có một số tự nhiên tròn trăm

c) Biến đổi thành hiệu của hai số tự nhiên trong đó có một số tự nhiên tròn trăm

d) Áp dụng hằng đẳng thức hiệu hai bình phương

Lời giải:

a) 38 . 42 = (40 – 2).(40 + 2) = 40² – 2² = 1 600 – 4 = 1 596.

b) 102² = (100 + 2)² = 100² + 2.100.2 + 2² = 10 000 + 400 + 4 = 10 404.

c) 198² = (200 – 2)² = 200² – 2.200.2 + 2² = 40 000 – 800 + 4 = 39 204.

d) 75² – 25² = (75 + 25).(75 – 25) = 100 . 50 = 5 000.

Bài 6 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Viết các biểu thức sau thành đa thức:

a) \({\left( {2x - 3} \right)^3}\)                                   b) \({\left( {a + 3b} \right)^3}\)                                  c) \({\left( {xy - 1} \right)^3}\)

Phương pháp:

Áp dụng hằng đẳng thức Lập phương của một tổng, một hiệu

Lời giải:

a) (2x – 3)³

= (2x)³ – 3.(2x)².3 + 3.2x.3² – 3³

= 8x³ – 36x² + 54x – 27.

b) (a + 3b)³

= a³ + 3.a².3b + 3.a.(3b)² + (3b)³

= a³ + 9a²b + 27ab² + 27b³.

c) (xy –1)³

= (xy)³ – 3.(xy)².1 + 3.xy.1² – 1³

= x³y³ – 3x²y² + 3xy – 1.

Bài 7 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Viết các biểu thức sau thành đa thức:

a) \(\left( {a - 5} \right)\left( {{a^2} + 5a + 25} \right)\)                  b) \(\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right)\)

Phương pháp:

Biến đổi biểu thức về dạng vế phải của hằng đẳng thức tổng, hiệu hai lập phương.

Lời giải:

a) (a – 5)(a² + 5a + 25)

= (a – 5)(a² + a.5 + 5²)

= a³ – 5³

= a³ – 125.

b) (x + 2y)(x² – 2xy + 4y²)

= (x + 2y).[x² – x.2y + (2y)²]

= x³ + (2y)³

= x³ + 8y³.

Bài 8 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Viết các biểu thức sau thành đa thức:

a) \(\left( {a - 1} \right)\left( {a + 1} \right)\left( {{a^2} + 1} \right)\)                    b) \({\left( {xy + 1} \right)^2} - {\left( {xy - 1} \right)^2}\)

Phương pháp:

Áp dụng hằng đẳng thức hiệu hai bình phương.

Lời giải:

a) (a – 1)(a + 1)(a² + 1)

= (a² – 1)(a² + 1)

= (a²)² – 1²

= a⁴ – 1.

b) (xy + 1)² – (xy – 1)²

= [(xy + 1) + (xy – 1)].[(xy + 1) – (xy – 1)]

= [xy + 1 + xy – 1].[xy + 1 – xy + 1]

= 2xy.2

= 4xy.

Bài 9 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

a) Cho \(x + y = 12\) và \(xy = 35\). Tính \({\left( {x - y} \right)^2}\)

b) Cho \(x - y = 8\) và \(xy = 20\). Tính \({\left( {x + y} \right)^2}\)

c) Cho \(x + y = 5\) và \(xy = 6\). Tính \({x^3} + {y^3}\)

d) Cho \(x - y = 3\) và \(xy = 40\). Tính \({x^3} - {y^3}\)

Phương pháp:

a) Áp dụng hằng đẳng thức bình phương của một hiệu

b) Áp dụng hằng đẳng thức bình phương của một tổng

c) Áp dụng hằng đẳng thức tổng của hai lập phương

d) Áp dụng hằng đẳng thức hiệu của hai lập phương

Lời giải:

a) Ta có: (x − y)² = x² – 2xy + y²

                           = x² + 2xy + y² – 4xy

                           = (x + y)² – 4xy

Thay x + y = 12 và xy = 35 vào biểu thức trên ta có:

(x − y)² = 12² – 4.35 = 144 – 140 = 4.

b) Ta có: (x + y)² = x² + 2xy + y²

                           = x² – 2xy + y² + 4xy

                           = (x – y)² + 4xy

Thay x – y = 8 và xy = 20 vào biểu thức trên ta có:

(x + y)² = 8² + 4.20 = 64 + 80 = 144.

c) Ta có: x³ + y³ = (x + y).(x² – xy + y²)

                           = (x + y).(x² + 2xy + y² – 3xy)

                           = (x + y).[(x + y)² – 3xy]

Thay x + y = 5 và xy = 6 vào biểu thức trên ta có:

x³ + y³ = 5.(5² – 3.6) = 5.(25 – 18) = 5.7 = 35.

d) Ta có: x³ – y³ = (x – y).(x² + xy + y²)

                           = (x – y).(x² – 2xy + y² + 3xy)

                           = (x – y).[(x – y)² + 3xy]

Thay x – y = 3 và xy = 40 vào biểu thức trên ta có:

x³ – y³ = 3.(3² – 3.40) = 3.(9 – 120) = 5.(–111) = –555.

Bài 10 trang 22 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng \(5\)cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:

a) Chiều dài và chiều rộng tăng thêm \(a\) cm?

b) Chiều dài, chiều rộng, chiều cao đều tăng thêm \(a\) cm?

Phương pháp:

Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng \(5\)cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:

a) Chiều dài và chiều rộng tăng thêm \(a\) cm?

b) Chiều dài, chiều rộng, chiều cao đều tăng thêm \(a\) cm?

Lời giải:

Thể tích hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm là:

5³ = 125 (cm³).

a) Chiều dài của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Chiều rộng của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).5 = (5 + a)².5

                          = (5² + 2.5.a + a²).5

                          = (25 + 10a + a²).5

                          = 25.5 + 10a.5 + a².5

                          = 125 + 50a + 5a² (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 50a + 5a² – 125 = 5a² + 50a (cm³).

b) Chiều cao của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).(5 + a) = (5 + a)³

                                   = 5³ + 3.5².a + 3.5.a² + a³

                                   = 125 + 75a + 15a² + a³ (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 75a + 15a² + a³ – 125 = a³ + 15a² + 75a (cm³).

 Sachbaitap.com